Motion of a simple pendulum
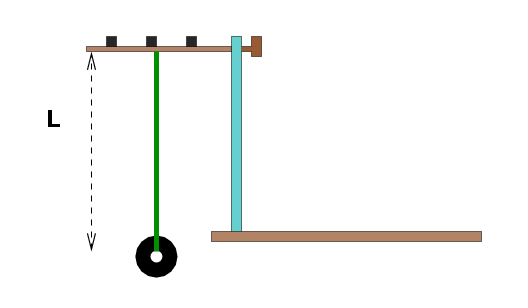
Use a simple pendulum to test SHM and measure the value of g.
- Set things up so that a 50-gram mass hangs from a long piece
of string. Run the string through one of the holes in
the 3-knob bar, and wrap one or two loops around a knob
to hold it in place.
Make sure that you can swing the mass freely when the string
is 80 cm long.
- Make measurements with at least 4 different lengths L,
ranging from about 7 cm to about 80 cm.
Measure the time to swing back-and-forth 10 times with
small angular amplitude: start at an angle of about
10 degrees from the vertical. Make 2 trials at each length.
- Make a neat table with your results,
showing the period, and period squared, in each case.
- Create one graph with your data.
Make a graph of the period squared versus the length of the string.
- Determine the slope of line connecting your measurements
and the uncertainty in the slope.
- Use the slope (and uncertainty) to compute a value for the
local acceleration due to the gravity (and its uncertainty).
Does your value agree with the standard one?
If you have time ...
- Use your graph to find the length of a pendulum which would
have a period of exactly one second.
Does that length have any significance?
- What is one simple modification you could make to improve
the precision of your value of g?

