Conservation of Angular Momentum

• If a rigid body rotates around a fixed axis, its angular momentum is oriented along the rotation axis
• It often helps to arrange the coordinate axes so that a body rotates in the xy-plane, so that angular momentum is entirely along the z-axis.
• When a rigid body rotates around a fixed axis, its angular momentum around that axis can be expressed as

               angular momentum = (moment of inertia) * (angular velocity)
          

• When a rigid body rotates around a fixed axis, the derivative with respect to time of its angular momentum around that axis can be expressed as

               dL/dt            = (moment of inertia) * (angular accleration)
                                = sum of external torques
          

• If the sum of external torques on a body around some axis is zero, then its angular momentum around that axis is constant.
• If such a body changes its moment of inertia, its angular velocity must change to keep angular momentum constant.

• Viewgraph 1

• Viewgraph 2

• Viewgraph 3

• Viewgraph 4

• Viewgraph 5

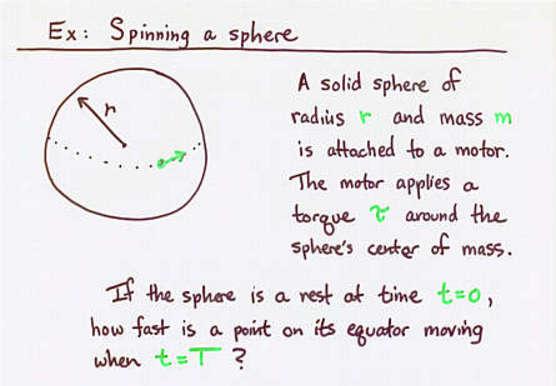• Viewgraph 6a

  
  
     Given  m = 500 kg, r = 10 m, torque = 600 N-m ccw,
     can you figure out at time T = 10 seconds
  
        a)  the linear speed of a point on the equator?
  
        b)  the rotational kinetic energy of the sphere?
  
        c)  the angular momentum of the sphere around its center?
  
  
  
  
  

• Viewgraph 6b

• Viewgraph 7

• Viewgraph 8

• Viewgraph 9

  In this performance by Miki Ando at the 2007 Worlds,

  • watch her spin at about 2:50 into the video
  • watch her prepare for a triple jump, and then jump and spin, at about 2:15 into the video

  ---

• Viewgraph 10

• Viewgraph 11

• Viewgraph 12