Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You remember the relationship between the change in Kinetic Energy of an object and the Work done by forces on it, right?
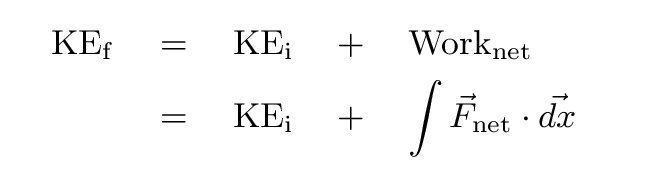
For example,
A chunk of ice of mass m = 2 kg sits motionless on a frictionless frozen pond. Then a breeze starts to push the ice cube with a constant force F = 3 N. After the chunk has slid 50 m, how fast is it going?
Well, there are very similar relationships between the angular analogues of these quantities: the change in rotational KE of an object and the Work done on it by torques.
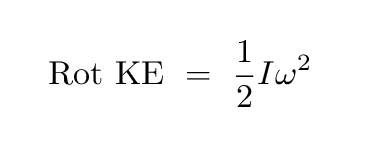
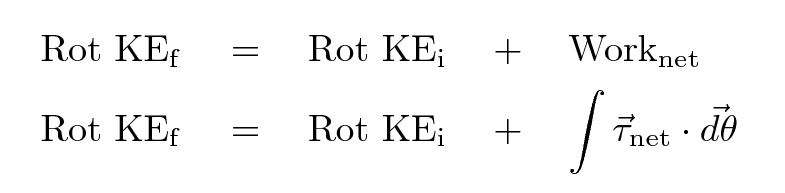
For example,
A giant grindstone with moment of inertia I = 700 kg*m^2 is spinning at 10 rpm. Joe slows it down by pressing a wooden brake against the rim of the wheel. How much torque must he exert in order to stop it within 5 revolutions?
Notice in the example above the fact that torque is involved in some vector arithmetic:
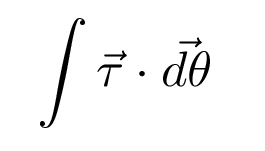
That means that torque must have some direction ... but what direction should it be? How does one figure out the direction of a torque?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.