Analysis of rolling motion using Torque

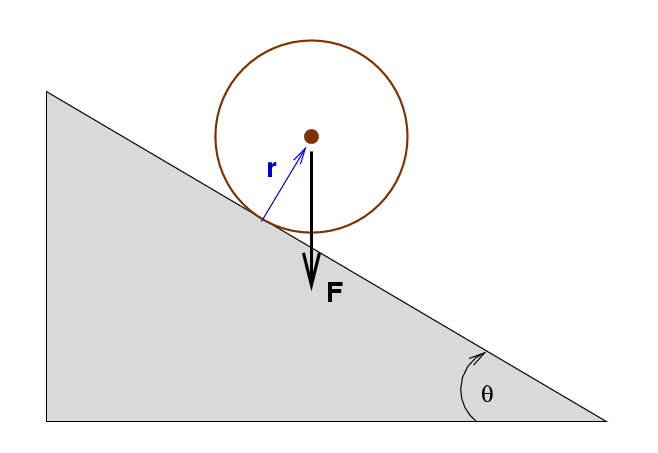
We can also look at rolling motion as a consequence of the torque on an object as it moves down a slope. Consider this hollow ball rolling down a ramp:

Gravity exerts a force F = mg on the center of the ball, directed vertically downwards. Now, if the ball is rolling without slipping, that means that the portion of the ball which touches the ramp is -- for a moment -- motionless. The ball rotates around this point of contact.

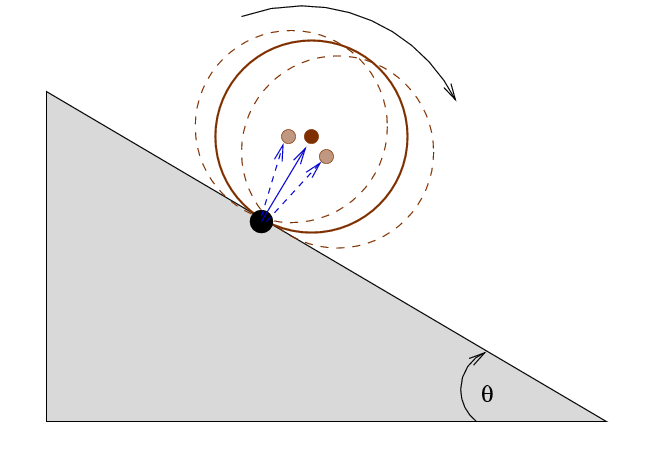
Therefore, we can look at the torque exerted around this point of contact by the force of gravity. Let's zoom in ...


  Q:  What is the torque around the point of contact?
      Provide both a magnitude and a direction.

  Q:  Express this torque in terms of the mass of the
      ball, M, and the radius of the ball, R.

  Q:  What is the moment of inertia of the hollow ball around its
      center of mass?

  Q:  What is the moment of inertia of the ball around its
      the point of contact with the ramp?

Now, how does the ball respond to this torque? Well, it has some moment of inertia, I, so the torque causes it to change its angular velocity. In fact, the angular acceleration must be



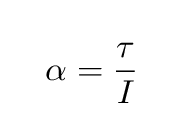
  Q:  Place the expression you derived for the magnitude
      of the torque in the top of this equation, and
      insert the moment of inertia around the point of contact in
      the bottom of the expression.
      What is the angular acceleration?


  Q:  Convert the angular acceleration to a linear acceleration.


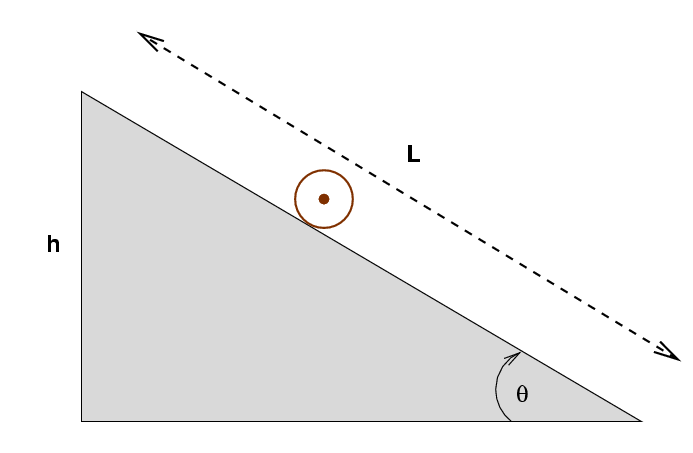
  Q:  If the ball starts at rest at the top of the ramp, what will
      its linear velocity be when it reaches the bottom of the ramp?
      Express the velocity in terms of the ramp's height h.