 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The parallel-axis theorem allows you to use SIMPLE pieces to build up the moment of inertia of a COMPLEX body. Let's do an example to see how it works.
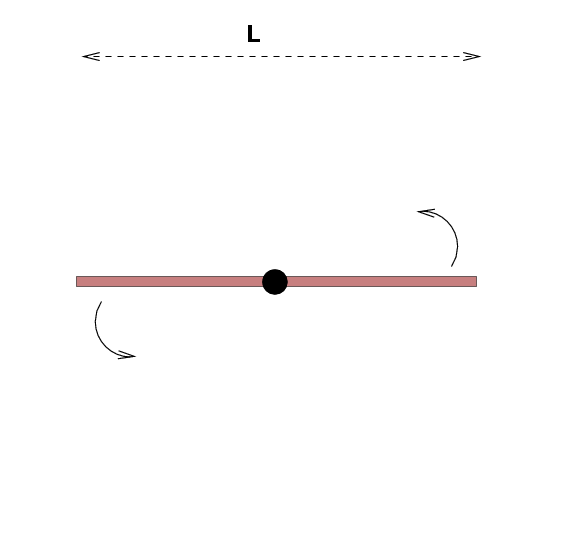
Start with a very simple object: a long, thin rod of mass m and length L, spun around its center.

What's the moment of inertia of this rod?

Now, suppose that I moved the rod away from the axis of rotation by some small distance x, like this:
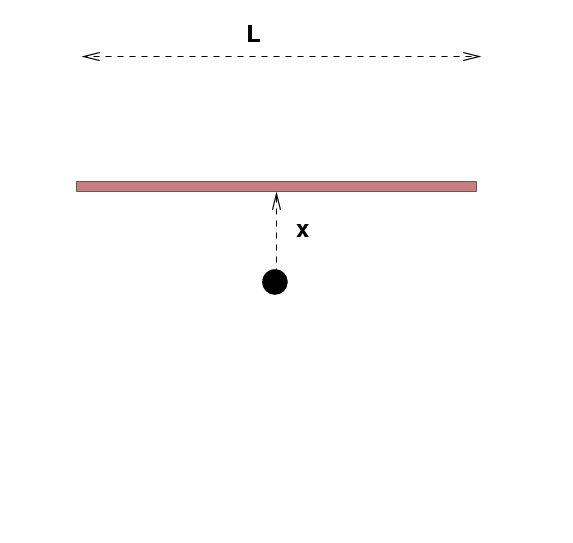
What's the moment of inertia of this displaced rod, if I keep rotating it around the same axis?
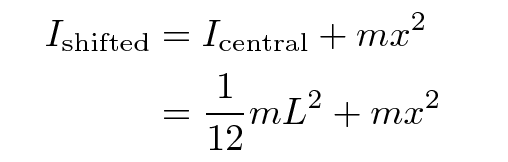
So, what if I combine two rods, making a compound object? Suppose I place the first rod centered on the axis, and the second rod offset by a distance x. What would the total moment of inertia of this 2-rod combination be?

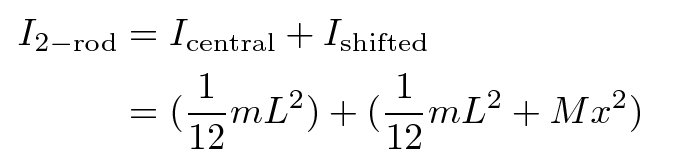
But why stop at just two rods? I can use this same technique to build up a large structure out of many rods, and compute its moment of inertia, too.
For example, I could place a whole bunch of rods next to each other, to make a square plate.

Let's call the total mass of this entire rectangular plate M. It has surface area A = L x L = L2. We can define the mass per unit area to be

Now, to figure out the moment of inertia of this complex structure, I just consider one piece at a time. Let me pick one thin little rod, a distance x from the axis and of width dx.
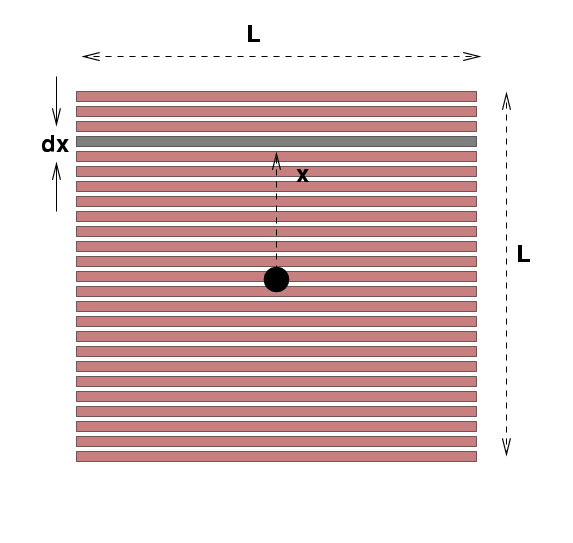
The mass of this little piece dM is
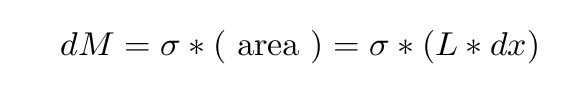
and the contribution of this piece to the moment of inertia must be
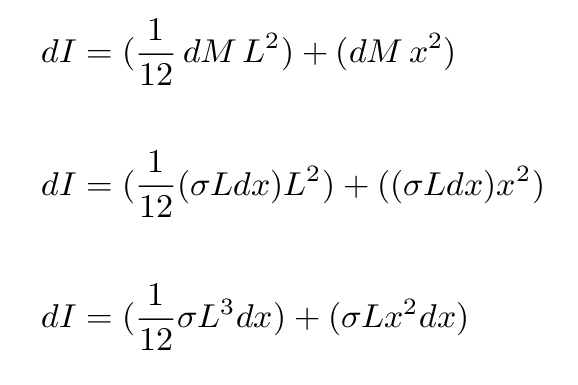
Okay, now it's your turn: figure out the moment of inertia of the entire square plate, adding up the contributions from all the little rods.
You can check your answers by looking at my own solution.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.