
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

For example, let's consider a long, thin rod of uniform density, with mass M and length r. The rod is is attached to a spinning hub at its left end.
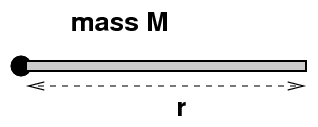
What we need to do is to break the rod into tiny little compact pieces ... because we know how to compute the moment of inertia of one compact little piece.
![]()
In fact, we need to break the rod up into an INFINITE number of VERY SMALL pieces; and that means it's time for calculus.


Okay, your turn. What happens if the density of the rod isn't uniform, but changes from one end to the other? Suppose that a rod has length L = 10 m and density
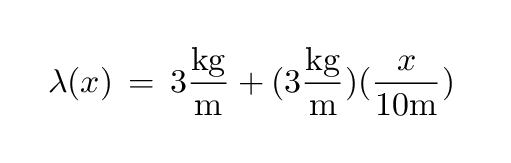
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.