Diffraction in astronomy (and how to beat it!)

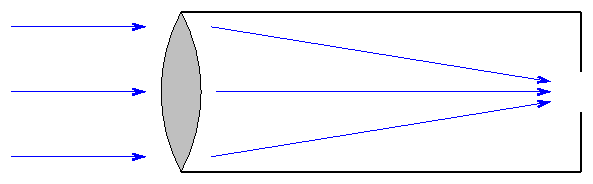
Most telescopes are (basically) devices which gather all the light within some aperture of diameter d and bring it to a focus.

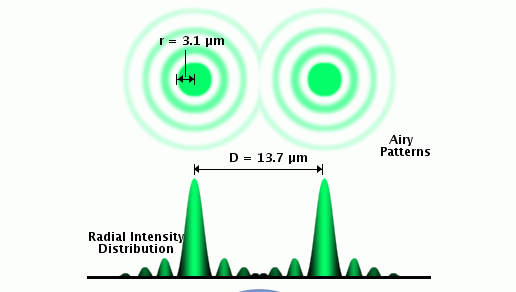
The limit to the angular resolution of a telescope is set by diffraction. Diffraction by a circular aperture causes a point source of light to be surronded by a series of rings, the analogs to the bright and dark spots you have seen when light shines through a rectangular slit.

Thanks to the Molecular Expressions site for this applet!

At some critical angle, the first dark ring in one object's pattern falls into the central bright spot of the other object's pattern. When that happens, one can't distinguish the two objects.

The critical angle turns out to be

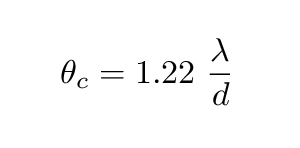
Any objects or features which have an angular size smaller than will be blurred together into a single fuzzy blob.

Consider the Hubble Space Telescope.

HST has an aperture of d = 2.4 meters. Suppose it takes pictures with visible light of wavelength lambda = 500 nm.



  Q:  What is the critical angle set by
      diffraction?



  Q:  Could HST take pictures of the Apollo
      hardware on the Moon which show any
      detail?


  Q:  HST is about the same size as certain
      spy satellites, which orbit the Earth
      at an altitude of roughly 300 km.  
      If a spy satellite
      were to take a picture of the RIT campus,
      could it see you as more than a blob?


  Q:  Could a spy satellite tell the difference
      between you and your roommate if the two
      of you were standing next to each other?

Our Sun is an interesting object -- especially at certain wavelengths, such as the 656 nm line called "Hydrogen alpha".

Can we see similar details on other stars?



      The nearest star system is Alpha Centauri:
      it takes light "only" 4.4 years to travel
      from Alpha Cen to us on Earth.


  Q:  How far is it to Alpha Centauri, in meters?
   
   
  Q:  One of the components of this triple star
      is about the same size as the Sun.  
      Could HST resolve the disk of this star?

Alas, no. The most "detaied" picture of any other star we have taken in visible light is this picture of Betelgeuse:

Beating the diffraction limit with interferometery

It turns out that there is a way to "beat" the diffraction limit, in a sense. If one combines the signals from two telescopes in the proper manner -- retaining all the phase and amplitude information on the waves detected by each telescope -- then the effective diameter of the instrument is equal to the SEPARATION of the dishes.

We call this technique interferometry, because the signals from the individual dishes interfere with each other when they are combined properly. It turns out to be very difficult to do this with optical light, but not so hard at longer wavelengths. Most of the interferometers used by astronomers work at radio wavelengths.

For example, the Very Large Array in New Mexico has dishes which are 25 meters in diameter. They typically collect radio waves at wavelengths of around 3 cm.



   Q:  What is the smallest angle a single dish
       can resolve?



   Q:  How does this compare to the resolution
       of HST in the optical?




   Q:  The longest baseline between dishes is
       36 km.  What is the smallest angle
       the entire array can resolve?

So the VLA is comparable to HST or other optical telescopes in its resolution. Here's an example: a false-color picture of the galaxies NGC 4038/4039. The optical image is shown in green (notice the stars), while the radio image is shown in blue (notice the gas).

But why stop there? One can (with a lot of effort) combine signals from radio dishes even farther apart. The Very Long Baseline Array (VLBA) consists of radio dishes scattered across North America and the Pacific.

The longest baseline in this array is about 5000 km.



   Q:  What is the smallest angle the VLBA
       can resolve?



   Q:  How does this compare to the resolution
       of HST in the optical?

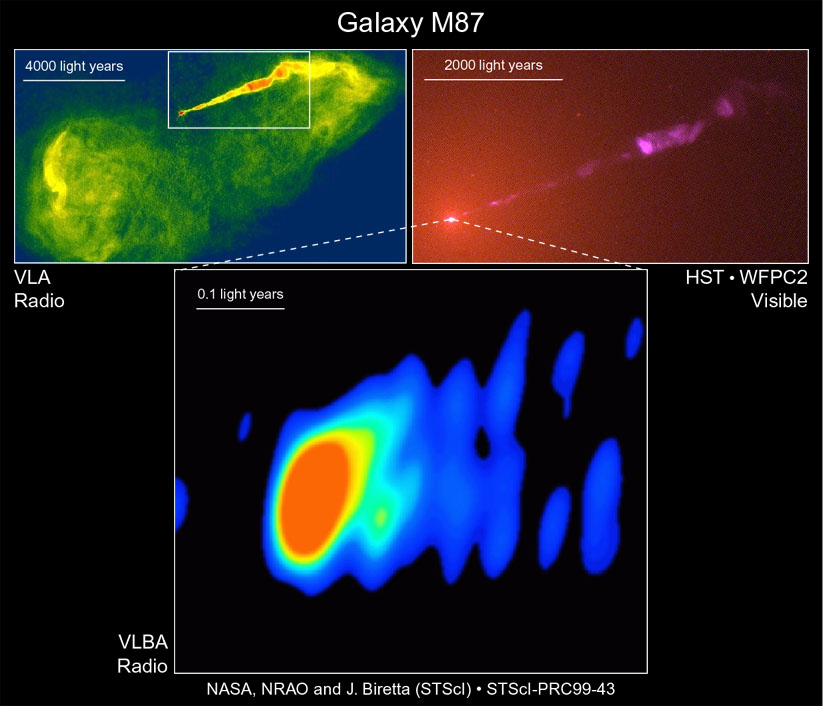
For example, the galaxy called M87 looks like a big, round ball of billions and billions of stars.

Image courtesy of NOAO/AURA/NSF

If you look closely, you'll see a faint little jet coming out from the center.

Image courtesy of Adam Block/NOAO/AURA/NSF

Compare these closeup pictures of the jet in the galaxy M87. You can find more details in an HST press release.