Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
If you shine a light through a SINGLE slit, you get a broad, fuzzy pattern on a distant wall.
If you shine a light through TWO slits, the pattern breaks up into more clearly defined bright and dark regions. And if you shine a light through MANY slits (a diffraction grating), you see a set of very bright dots separated by large spaces of complete darkness.
Why?
The answer lies in the mathematics of adding together many waves. We have tools that work for adding two waves, or maybe three waves, but not for tens or hundreds of waves. In order to make sense of the diffraction grating, we need to spend a bit of time learning a new tool for wave analysis: phasors. We can then come back to the question of the diffraction grating and answer it easily.
We can represent waves using equations:
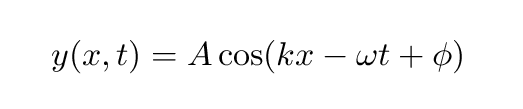
We can represent waves using pictures of wiggling lines:
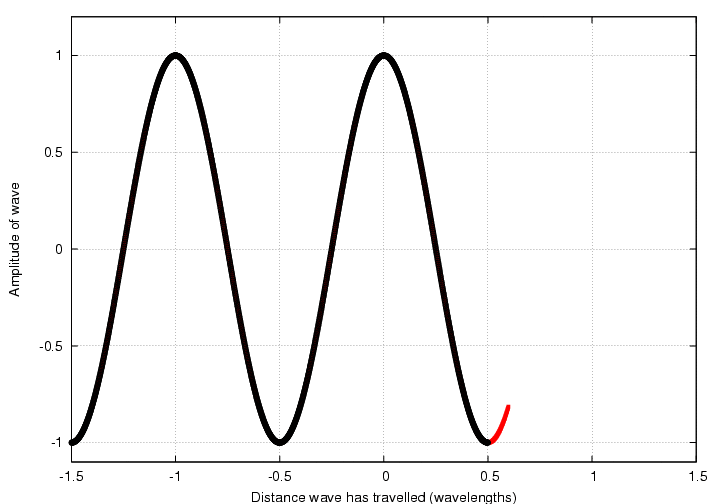
Today, we will come up with a new way to represent waves: by little clocks.
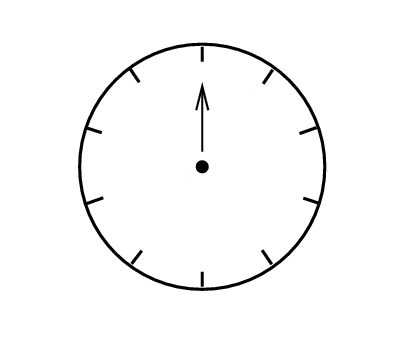
More specifically, we will use the position of the hand on the clock to tell us about the amplitude and phase of a wave at some given time. Let me illustrate with an example: watch as one particular wave propagates to the right:
Now, watch again as I put one of the little phasor clocks next to the graph.
The hand on the little clock rotates as the wave progresses -- the position of the hand says something about the amplitude of front of the wave, or something. In fact, there are several ways to interpret the position of the hand.
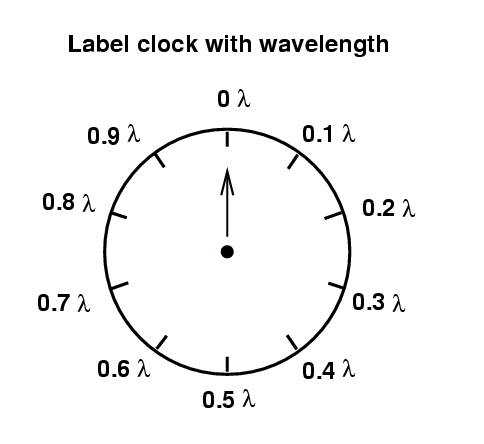
The position of the hand tells us how far the wave has moved since it was at its maximum positive amplitude.
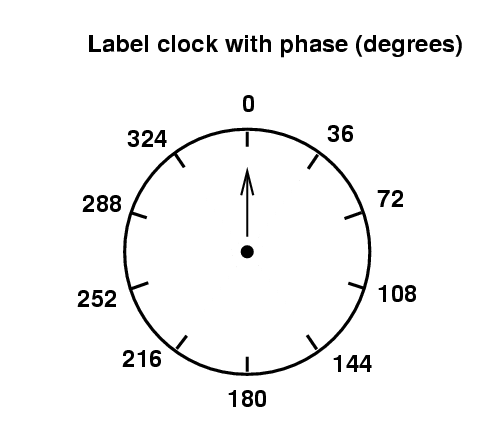
The position of the hand tells us the angular position of the wave -- in other words, the value of all the stuff inside the sine or cosine function.
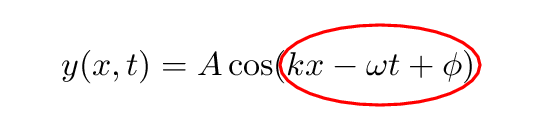
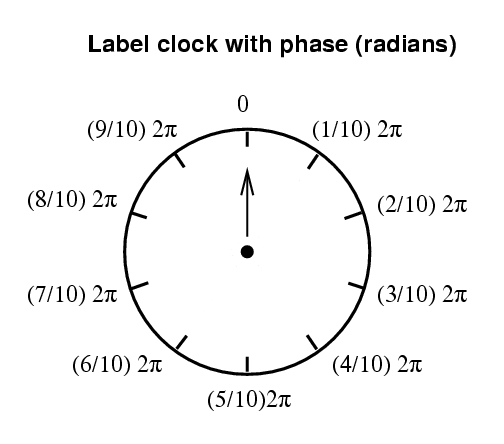
Of course, we can choose to think of this angular position in terms of degrees, or in terms of radians.
In summary, a phasor uses the hand of a little clock to represent the wave.
So, suppose someone gives us two waves and asks, "What happens when these waves meet? How do they interfere?"
One way to answer the question is to write down equations and use trigonometric identities and algebra ...
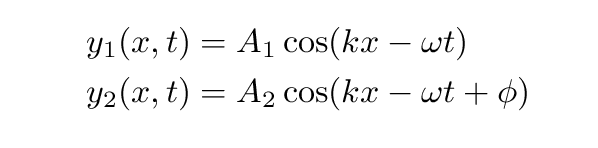
Another way to answer the question is to draw diagrams showing each wave function
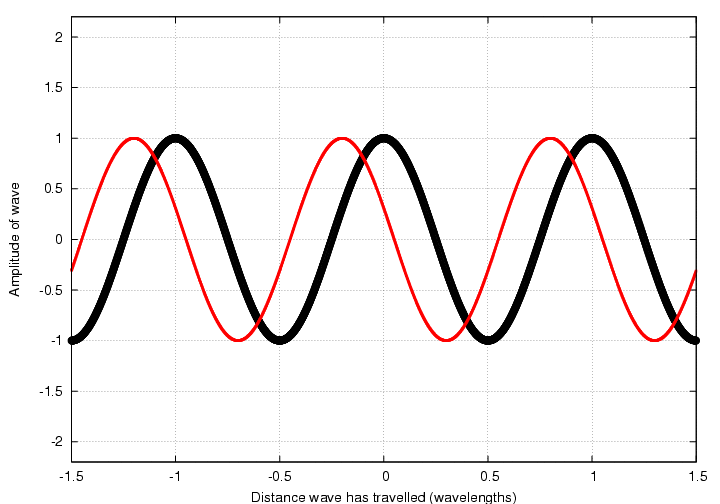
then read the values for each function from the graph, add them, and plot the result:
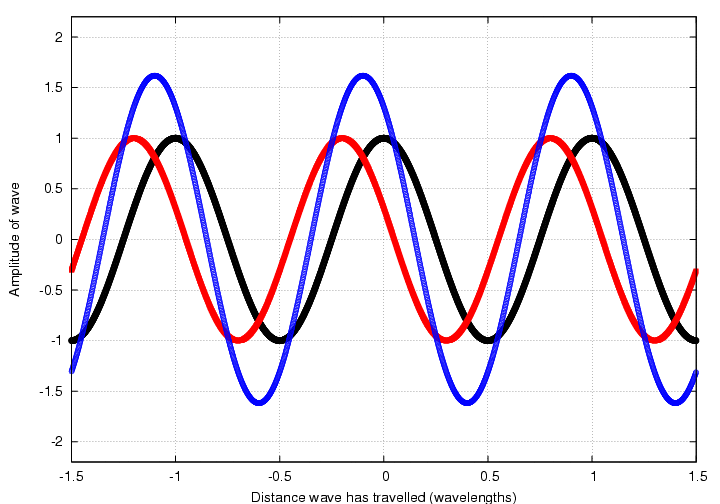
But perhaps the quickest and easiest way to do this is to draw little phasor clocks for each of the waves:
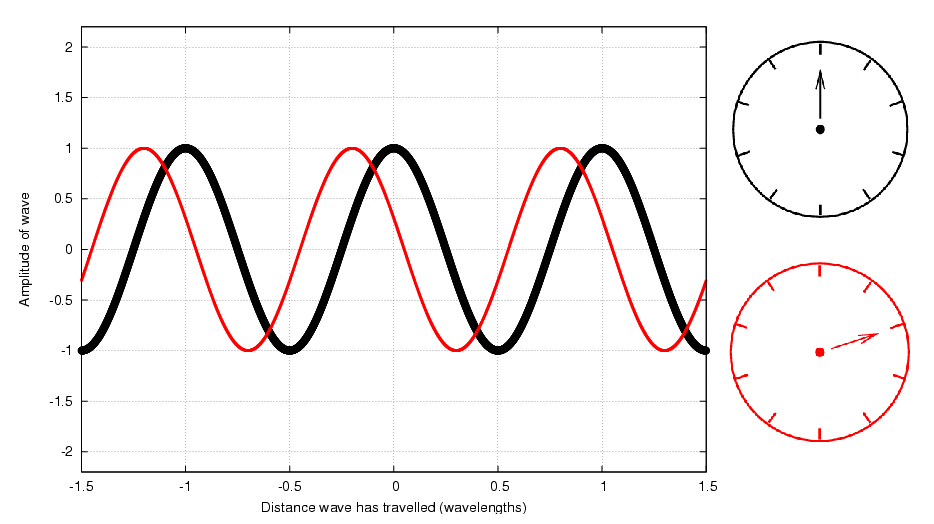
and then use the clocks themselves to do the addition. There is a very simple way to find the sum of two waves using phasors: just treat the little hands as vectors and add them:
Q: Call the amplitude of the black wave A.
What is the amplitude of the wave
which is the sum of the red and black waves?
Q: What is the phase of this sum relative to the
black wave?
Let's check your answers by looking at the wave pictures:
Okay, now let's take another look at interference patterns of two slits, three slits, and many slits.
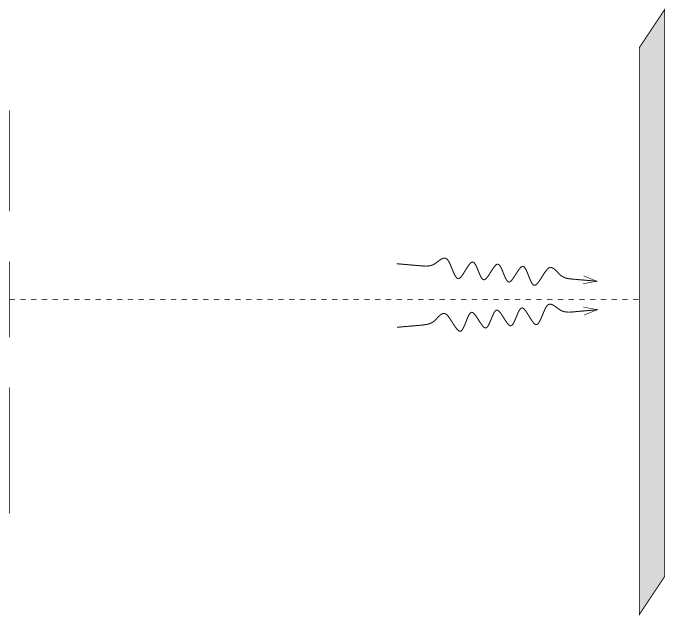
The simple two-slit experiment looks like this: all we need to consider are two waves which enter the slits in phase:
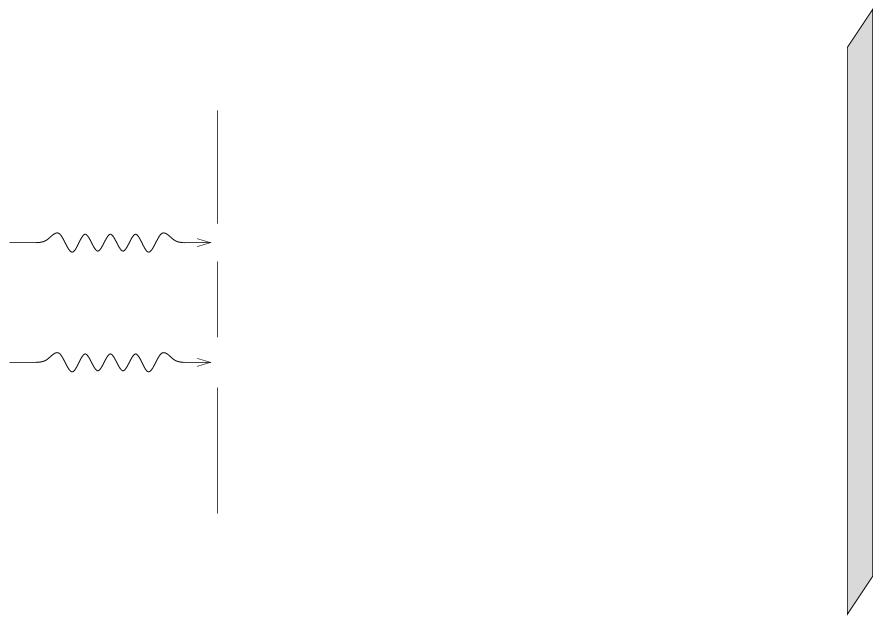
If we look at the very center of the far screen, the waves travel exactly equal distances, meet in phase, and create a bright spot.
Let's add phasors to the picture. The two waves start in phase:
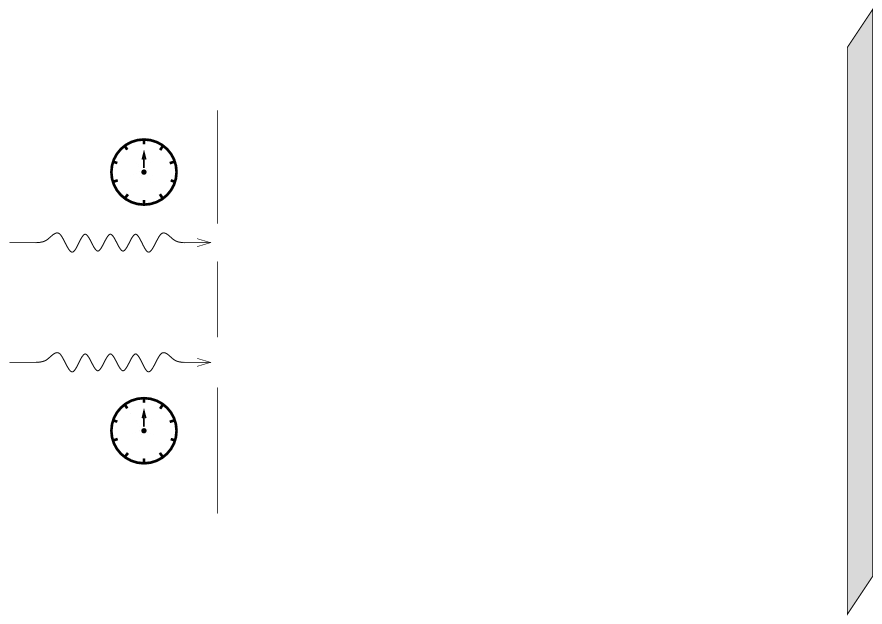
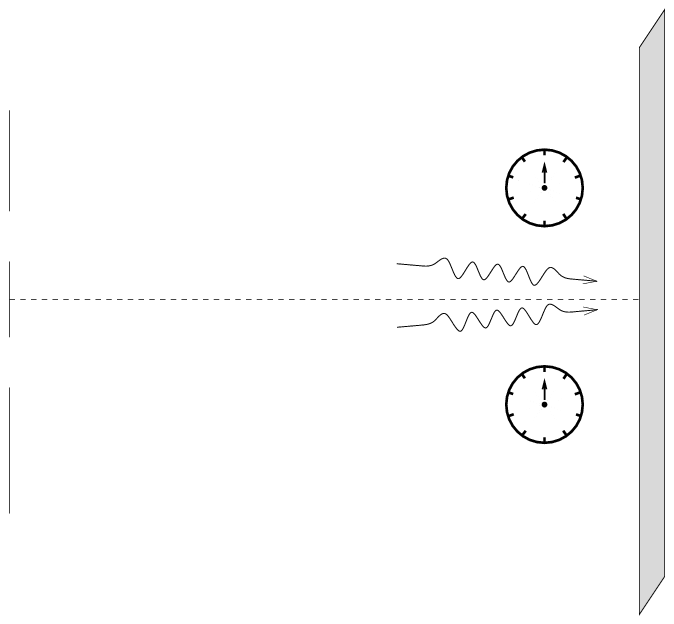
... and are still in phase when they meet at the screen:
Q: Call the amplitude of each wave A.
What is the amplitude of the
sum of the two waves?
Now, let's look at some point off-center. Suppose we pick the point on the screen which has the first bright spot away from the center:
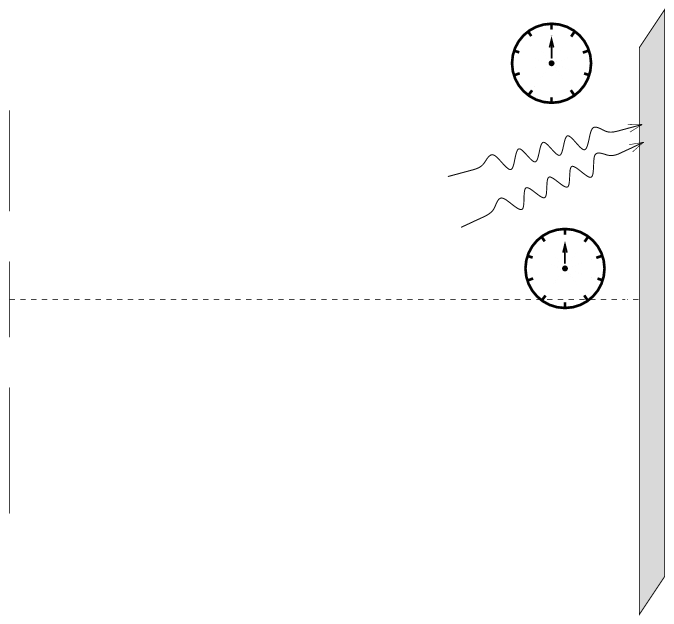
Once again, the waves are in phase when they meet. No problem.
But -- what happens if we pick a location on the screen which is in between the brightest spots?
If we move 1/4 of the way from the central bright spot to the next bright spot, the two waves won't meet in phase any more. How far out of phase will they be? It turns out that the fraction of the distance between spots on the wall is the same as the fraction of the extra wavelength travelled by one of the waves.
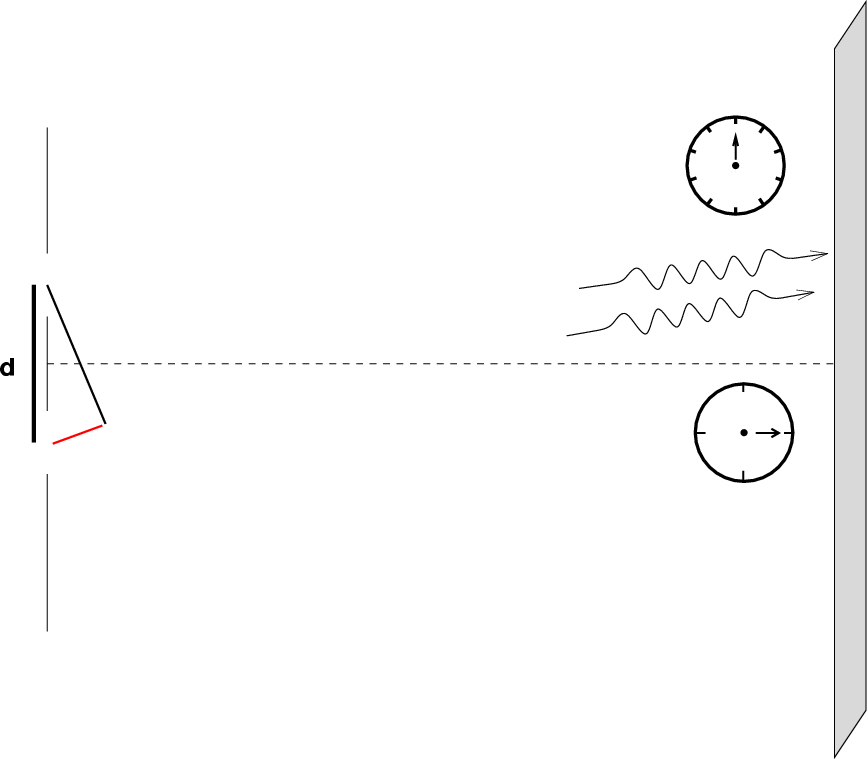
Q: Call the amplitude of each wave A.
What is the amplitude of the
sum of the two waves?
Q: How does this amplitude compare to
the amplitude of two waves meeting
perfectly in phase?
Now, let's increase the number of slits from two to three. Now there are THREE waves meeting at the screen. We can figure out the phasor clock for the third wave pretty easily.
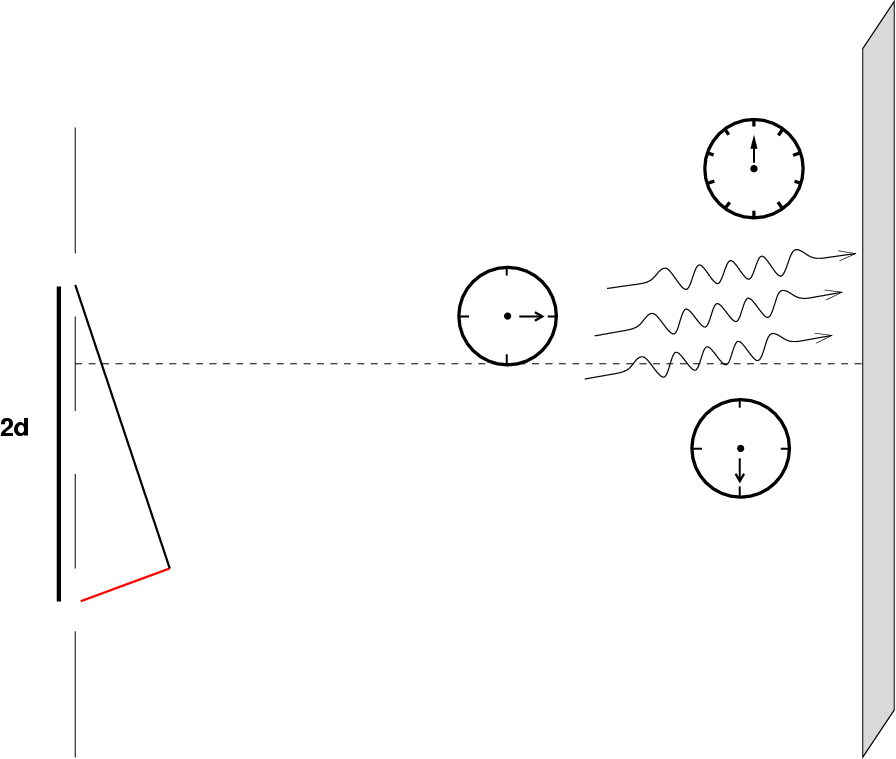
Q: Call the amplitude of each wave A.
What is the amplitude of the
sum of the three waves?
Q: How does this amplitude compare to
the amplitude of three waves meeting
perfectly in phase?
Now, let's increase the number of slits from three to four. Now there are FOUR waves meeting at the screen.
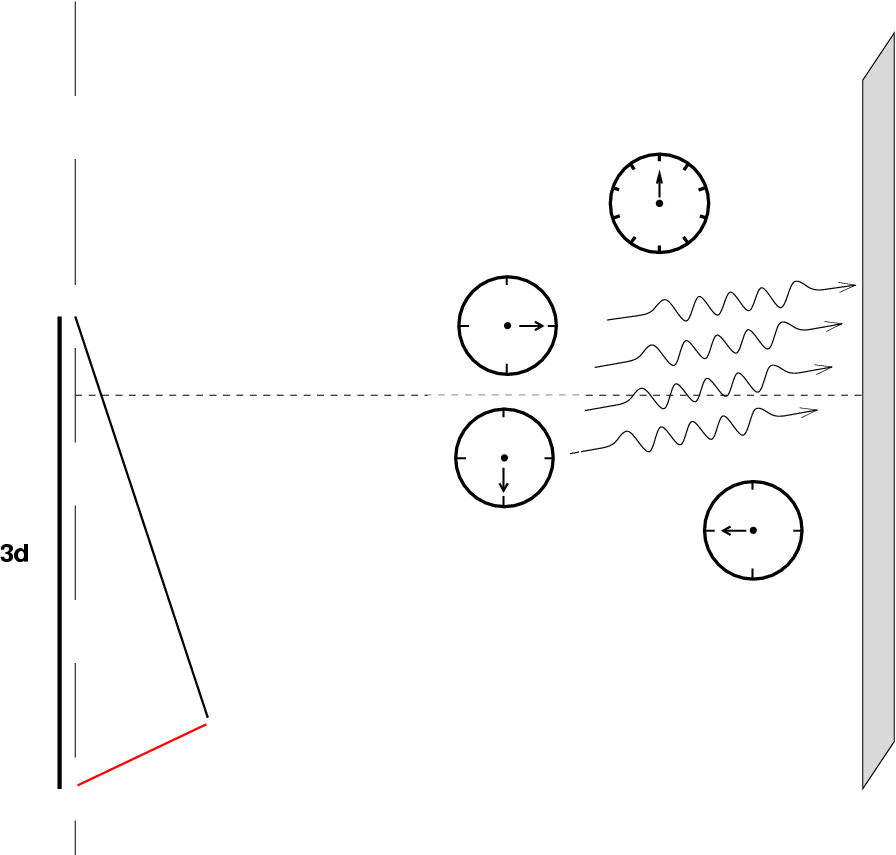
Q: Call the amplitude of each wave A.
What is the amplitude of the
sum of the four waves?
Q: How does this amplitude compare to
the amplitude of four waves meeting
perfectly in phase?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.