 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Your job is to use a diffraction grating to measure two wavelengths:
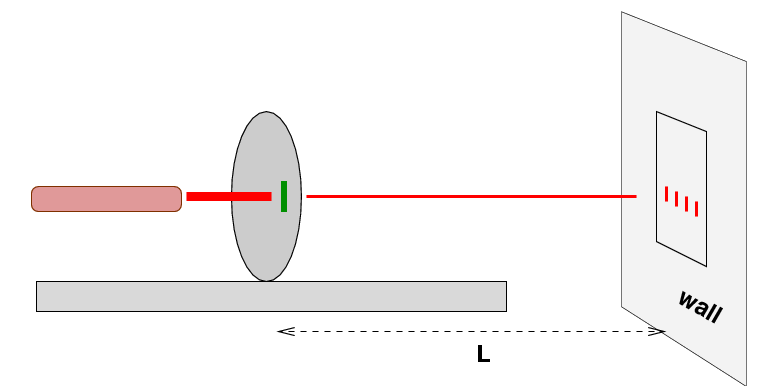
The first involves the same procedure you've used in the recent past: shine laser light through a device and measure the separation of bright or dark spots on a distant screen:

Set up an optics bench and laser as shown above. Instead of shining the laser through a wheel, shine it through a diffraction grating which sits on an optics component carrier. Place a piece of paper on the wall, and arrange things so that you can mark on a piece of paper the central bright spot and one spot to the side. The distance L will probably be smaller than you've used in the past -- perhaps 50 or 60 cm.
If all went well, your value for the wavelength of laser light should be similar to, but more precise than, your earlier measurements.
Remove the diffraction grating from the optical bench and hold it carefully in your hand, a few inches in front of one of your eyes. Look through it at the spot formed by the laser on the wall.
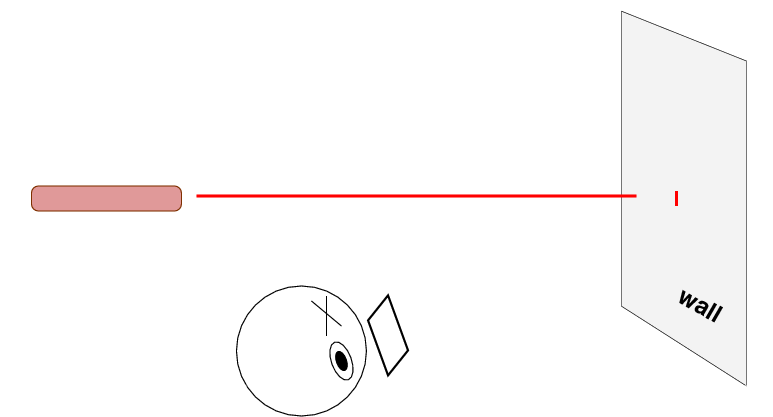
Now, hold the grating in front of your eye as you look at the lamp sitting on the desk at the front of the room.
Hint: Sample Problem 36-6
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.