Joe wraps a rope several time around the barrel, and attaches the end of the rope to a bucket of mass m = 5 kg. The bucket hangs motionless H = 2.5 m above the ground because Joe is holding onto the barrel.
At time t = 0, Joe releases the barrel. The bucket starts to fall downwards, pulling on the rope and causing the barrel to spin. As the bucket falls, the barrel spins faster and faster.
How long does it take the bucket to reach the ground?
- the answer
- detailed solution: part I part II part III
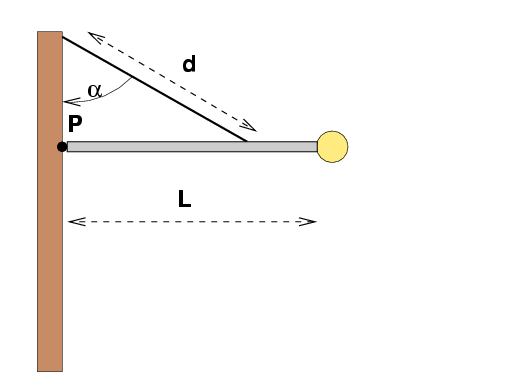
- When the flagpole is in equilibrium, what is the tension in the wire?
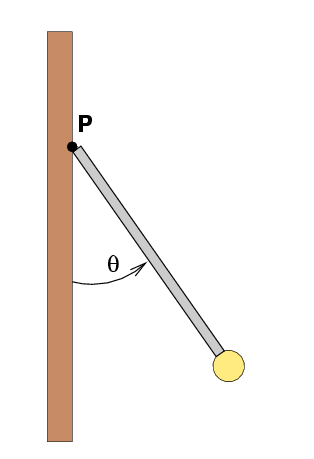
- When the pole has swung so that there is an angle theta = 20 degrees remaining between it and the wall, what is the pole's angular acceleration around the hinge?
- Is the motion of the pole an example of simple harmonic motion?
- Just before the pole slams into the wall, what is the linear speed of the golden ball?
The wire breaks! The pole starts to swing downwards around the hinge without friction of any kind.
- the answers
- detailed solution: part I part II part III part IV

- Jane has initial speed 4 m/s. What speed should Fred have?
- What is their initial angular momentum around point "X"?
- What is their moment of inertia around point "X"?
- What is their angular speed?
- What are their linear speeds?
- What is their rotational KE?
- What is their angular speed now?
- What is their rotational KE now?
It works! They are now holding hands and spinning around point "X", Jane AJ from the center and Fred AF from the center.
To end their program, they pull each other close, until their centers of mass are only bJ = 0.28 meters and bF = 0.21 meters from point "X".
- the answers
- detailed solution: part I part II part III

Fred now turns the disk a small distance theta from its resting position and releases it. The disk starts to oscillate back and forth.
- Show that the motion of the disk is SHM.
- What is the period of the motion?
- the answers
- detailed solution: part I part II