The center of mass of an extended object

In real life, many objects are extended: they contain matter distributed somewhat uniformly over large distances. They don't look much like little compact balls, so it's not so easy to use the discrete approximation to calculate their centers of mass.

Consider the shape outlined on this piece of graph paper:

You CAN find the center of mass in the same old way, if you wish: treat each little square of material as an individual bit of matter with mass 1 unit.

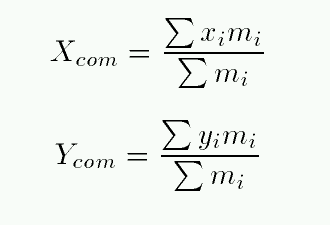
Find the total number of squares contained in the object; that is the object's total mass.
Treat the top-left corner of the object as the origin, where x = 0 and y = 0. Use each little square's x-position and y-position to calculate the center of mass:

You can also find the center of mass by breaking the irregular object up into regular pieces, finding the mass and center of each piece, and then treating each piece like a little ball at its center.

Pick any method you like, but please find the location of the center of mass of this object, and mark it with an "X". How many squares from the top-left corner is the center of mass?

But for really complicated objects, there's no way around it: in order to find the center of mass, you have to integrate.

How to deal with extended objects: integrate!

Now it's your turn to find the center of mass of an extended object.

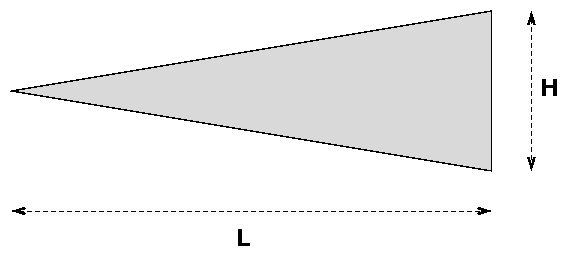
A long, thin triangle of length L and base H is made of a uniformly dense material. Where is its center of mass? (Hint: the location of the center of mass is easy to find in one direction using symmetry ... but you must do the integral to find the center of mass in the other direction).