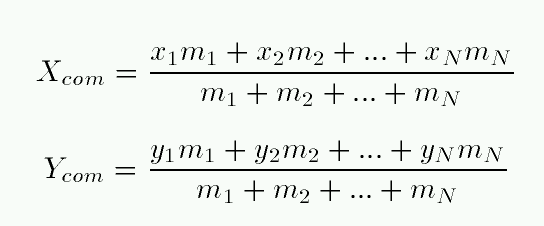
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
If we have a collection of compact little balls, then we can find their center of mass with a simple sum:
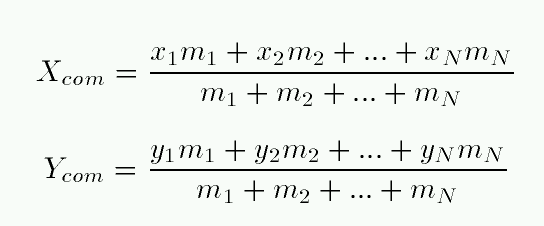
Or, in a more compact notation,
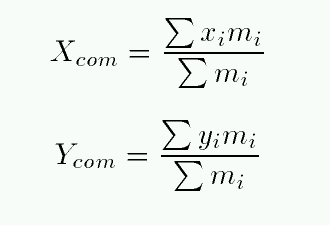
But what if we need to find the center of mass of a more complex object -- one which has a continuous distribution of material?


There is a technique we can use: integrate the contribution to the center of mass of each little bit of the object. Let's see how that works by starting with a very simple example and working our way to more complicated ones.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.