Impulse and momentum

In this experiment, you will measure forces exerted over time on a cart as it bounces off an obstacle. Your job is to figure out the pre-bounce and post-bounce velocities of the cart, calculate the change in its momentum, and compare that to the impulse.

First, prepare by turning on the computer at your table and running the LabPro software.

in the "Student Shares" -> ... -> "LabPro" folder, copy the cart_impulse file to the Desktop, then double-click it to start LabPro
connect the force sensor to the CH1 port on the LabPro interface
calibrate the force sensor on its +/- 50 N setting

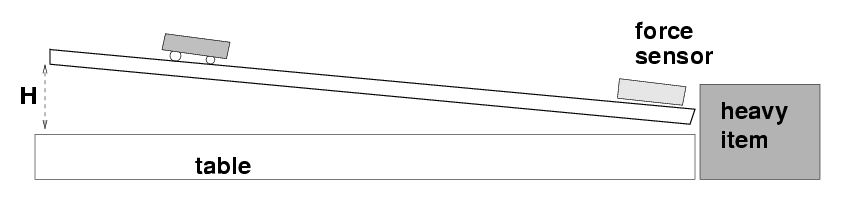
Now, set up a track so that one end is slightly higher, at an angle between 3 and 4 degrees. Draw a picture and show your calculations for the angle.

Remove the hook from the force sensor and replace it with the rubber bumper. Place the force sensor at the bottom end. Put two mass bars or other heavy weights into the force sensor to hold it in place (you might even tape it into place on the track). Make sure that a heavy item sits next to the bottom end of the track to prevent the track from sliding across the table.

measure the tilt of the track accurately
arrange the cart so that its spring-loaded bumper is extended and will bump into the force sensor's bumper
measure the mass of your cart

Put the cart so that the end of the plunger is 45 cm from the sensor. Call this your "starting point."

An object falling freely downwards accelerates at g = 9.8 m/s^2. What is the acceleration of an object sliding down your track without friction?
Given this acceleration, and the distance it travels, how fast will the cart be going when it bumps into the sensor? (Hint: one of the 1-D kinematic equations can help you out ...)

Prediction phase

Minimize the LabPro window -- we are not going to use the sensors yet.

To make one set of measurements, release the cart from its starting point. The cart should roll down, bump into the force sensor, bounce off and roll back up the ramp. Watch carefully and mark the location it reaches at the apex of its motion.

Make three trial runs. Create a table showing all your results. How consistent are the results from one run to the next?

Again ignoring friction, how fast was the cart moving as it started back up the track after the bounce? Compute three speeds, one for each trial.
Draw a series of three pictures showing the cart and sensor just before, during, and just after they collide
What is the change in the cart's momentum? Be careful to get all your signs correct.
Using the average change in momentum, predict the impulse given to the cart by the bumper.
Use the uncertainty in the initial position of the cart to determine the uncertainty in the distance it rolled down.
Use the range of final positions of the cart in the three trials to determine the uncertainty in the final position.
Use those uncertainties to compute the uncertainties in the cart's velocities (initial and final) at the sensor.
Use those uncertainties to compute the uncertainty in the change of momentum of the cart.

When you have reached this point, call over an instructor to check your prediction.

Truth or consequences phase

We will now find out how well you can predict the impulse given to the cart.

Maximize the LabPro window. Place the cart at the same starting point you used earlier. Press the Collect button on LabPro, and release the cart. The cart will roll down, bounce off the bumper, and roll back up the ramp. Measure the final position of the cart and mark it down.

LabPro should show you a graph like this:

You can calculate the impulse on the cart by integrating the area under the curve: that will integrate force over time during the collision.

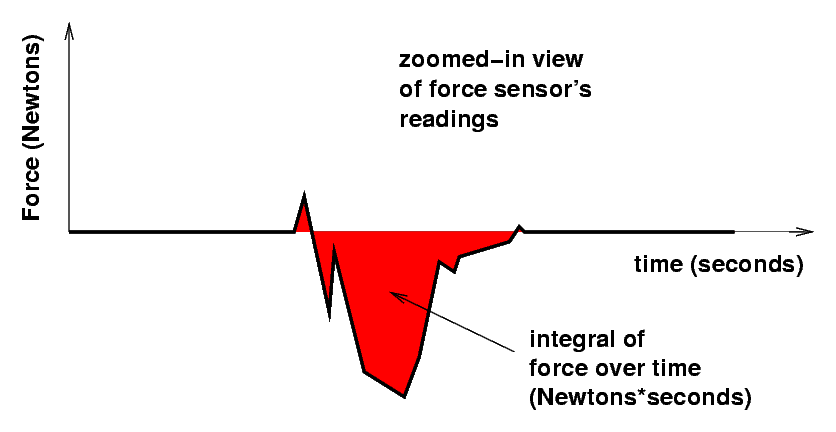
use LabPro's Integrate function to find the impulse by integrating the area under the force-time curve. Select just the portion of the data around the impact.

Compare the impulse given to the cart by the bumper (from the graph of force versus time) to your prediction (based on the cart's velocity before and after the collision). Do the computed impulse values agree with the measured impulse value(s) within this uncertainty?

perhaps it would help to review the propagation of errors ...

Hand in your answers to all these questions, written neatly. Include a table with ALL your measurements, and include all your calculations, too.