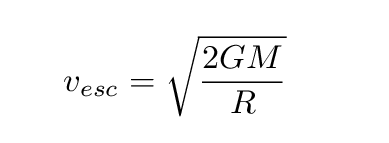
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
We have seen that one can compute the escape velocity from a body via
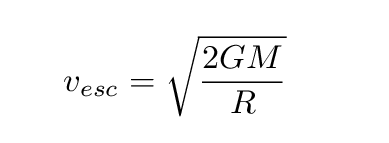
What happens if we take a massive object -- like the Earth -- and squeeze it down into a smaller size?
Suppose that Earth's radius were only R = 60 km. What would its escape velocity be?
Suppose that Earth's radius were only R = 150 m. What would its escape velocity be?
Image of Bobby Doerr autographing a baseball
courtesy of ESPN
Suppose that Earth's radius were only R = 10 cm. What would its escape velocity be?
If we keep squeezing and shrinking the Earth, we eventually reach a critical point: the escape velocity reaches c, the speed of light.
If an object somehow becomes this small, then light rays from its surface cannot get away. The object would become .... black.
Image of Bobby Doerr autographing a baseball
courtesy of ESPN
We call such extremely dense objects black holes, because
Q: What would happen to the Earth
if the Sun were suddenly
to collapse into a black hole?
A: It would grow cold.
But it would not "get sucked into"
the black hole. The gravitational
force of the Sun would remain
just the same as it is now.
Ordinary objects do not, and can not, turn into black holes. However, certain types of stars can and do! For example, a star which starts its life with about 20 times the Sun's mass will eventually run out of nuclear fuel at its core; when that happens, the core will collapse into a black hole (yes, I'm simplifying :-)
One reason that black holes CAN be dangerous is simply because they are very small, and therefore, it is possibly to approach one very close. If one comes very close to a massive object, then the differences in its gravitational force on different parts of your body can become important ... or even painful.
Let's see how that works:
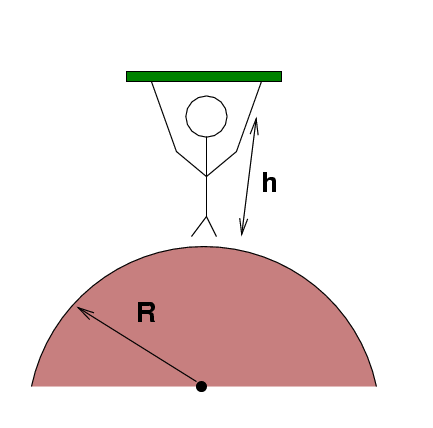
Joe hangs by his hands from a bar. The Earth, with radius M = 5.98 x 10^(24) kg and radius R = 6,370,000 m, pulls on all parts of his body. Since his feet are a bit closer to the center of the Earth than his head, the gravitational force is stronger on his feet than his head.
Assume that Joe's feet and head both have mass m = 5 kg, and that Joe's height is h = 2 m.
Now, suppose we change the arrangement a bit: we take Joe to planet X, which is smaller than Earth. Planet X has M = 1.47 x 10^(17) kg and radius R = 1000 m.
We change it one more time: Joe hangs above a tiny sphere of very dense material. The sphere has M = 1.47 x 10^(13) kg and radius R = 10 m.
The magnitude of the tidal forces exerted by an object depends on the change in gravitational force as one moves away from the object: if the gravitational force changes quickly, then the tidal forces are large. Mathematically speaking, we can say
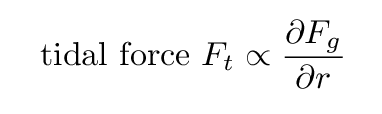
Q: As you travel towards a black hole,
you notice a strain of about 50 N
between your head and feet.
You quickly manuever your spaceship
to double the distance between you
and the black hole.
How big is the strain between your
head and feet now?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.