 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
A really SMALL rollercoaster
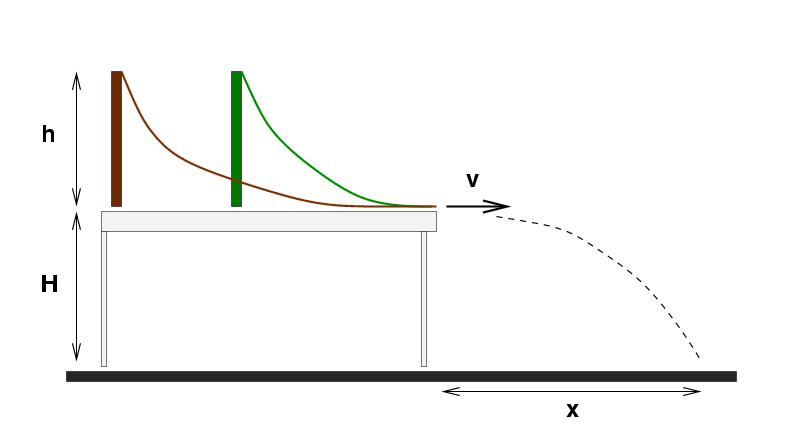
Let's build our own very small roller coaster here
in the classroom. I'll set up a pair of towers,
each of height h above the tabletop.
A car of mass m will roll down the track from each tower
to the edge of the table, then fly outwards
with some initial horizontal velocity v.
As it falls a distance H to the floor,
the car will cover a horizontal distance x.
First, compute some quantities in general:
use symbols only, no numbers.
- Write an expression for the kinetic energy,
potential energy, and total energy of
the car when it is motionless at the top of the track.
What is the origin of your coordinate system?
What is the zeropoint of your potential energy?
- Write an expression for the kinetic energy,
potential energy, and total energy of the
car when it is about to fly off the table.
- What will the car's velocity v be when
it flies off the table?
- How far x will the car move horizontally
as it falls to the floor?
- Does this distance depend on the mass of the car?
- Does this distance depend on the value g,
the local acceleration due to gravity?
Now, I'll give you the quantities for the actual
equipment in our example; that is, the height h,
etc.
- What is the car's total energy?
- What will the car's velocity v be when
it flies off the table?
- How far x will the car move horizontally
as it falls to the floor?
- Should each track produce the same distance x?
At this point,
we will run several trials to measure the actual
distance the car flies after running down
each of the two tracks.
I'll write down the results on the board for everyone
to see.
If we have time ...
- Did the actual distance(s) match your predicted distance?
If not, why not?
- Was there a difference in the distances produced
by each track?
If so, why?
- Look at the difference in x between the two tracks.
You can use it to estimate the coefficient of rolling
friction between car and track.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.