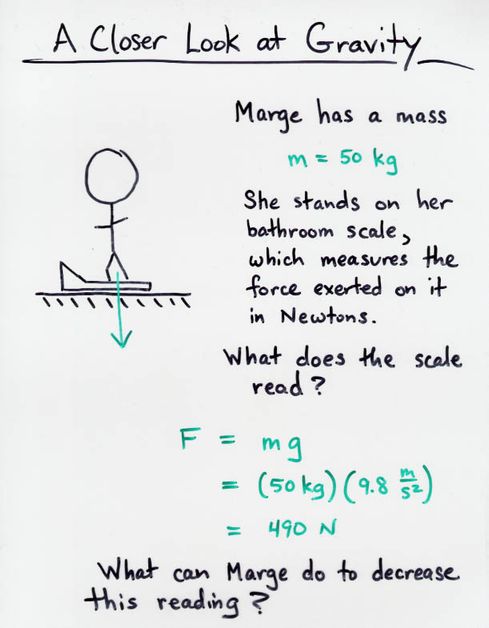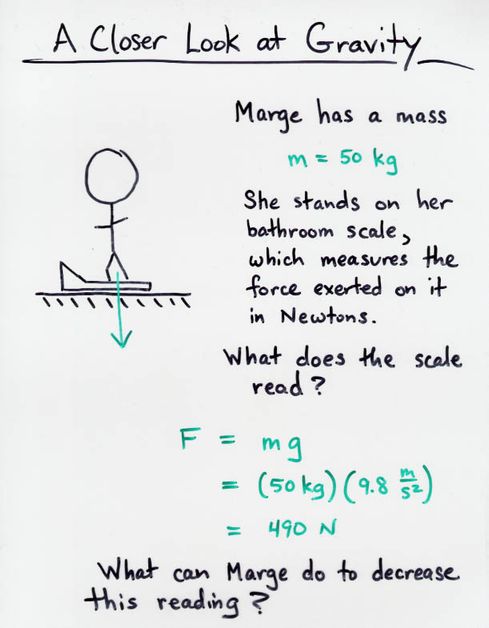The force of universal gravitation

The familiar equation for the force of gravity on an object on the Earth's surface

        F   =  m * g

is really just a simplified version of a more general expression ....

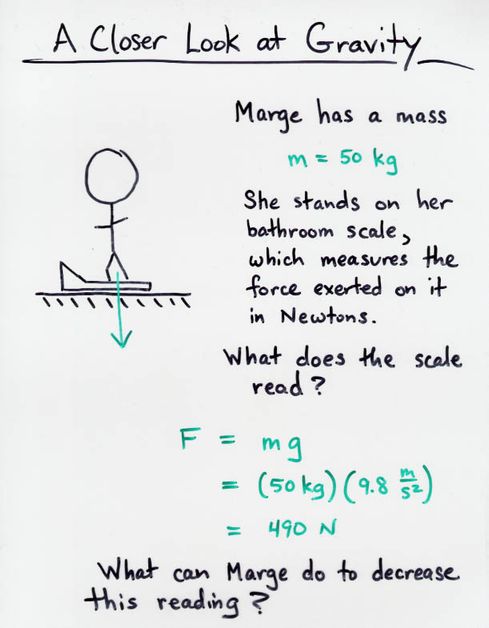
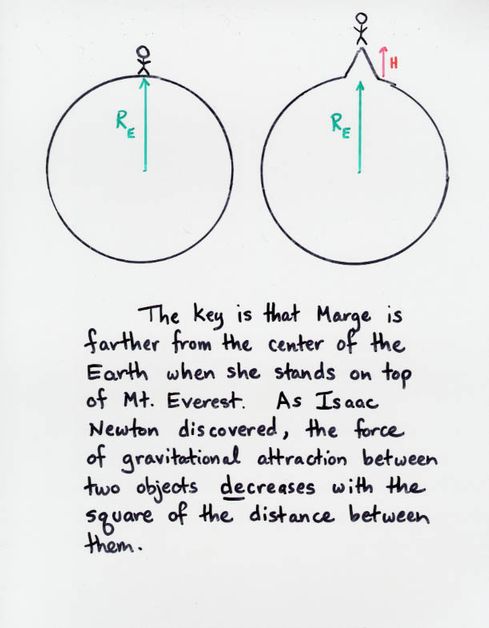
Newton, the apple, and the Moon

The story -- who cares if it's true? -- goes like this: Isaac Newton was sitting outside on a nice day, thinking deep thoughts, when he noticed an apple fall from a nearby tree. His glance went from the apple to the Moon, which was visible in the sky at that moment. "Is it possible," he wondered, "that the same force which caused the apple to fall (to the ground) could also be causing the Moon to fall (around the Earth)?".

Let's follow his subsequent reasoning....

1. The apple part ...
   1. What is the acceleration of the apple downwards towards the ground?
   2. How far is the apple from the center of the Earth?
   3. How far is the Moon from the center of the Earth?
   4. How many times farther from the Earth is the Moon?
   5. If the force (and acceleration) go like the inverse square of the distance, what would this acceleration be if the apple were at the distance of the Moon?

2. The moon part ...
   1. What is the period the Moon's orbit around the Earth, in seconds?
   2. What is the circumference of the Moon's orbit?
   3. What is the average speed of the Moon in its orbit?
   4. What is the acceleration of the Moon in its orbit?

If Newton actually followed this line of reasoning, what could he conclude about the force exerted by the Earth on the apple and the force exerted by the Earth on the Moon?

Gravity and vectors

The force of gravity has both a magnitude and a direction. The magnitude is given by Newton's equation. The direction is always attractive, along the line connecting the two objects.

That means that sometimes you need to break the force into components ....

Example 1:

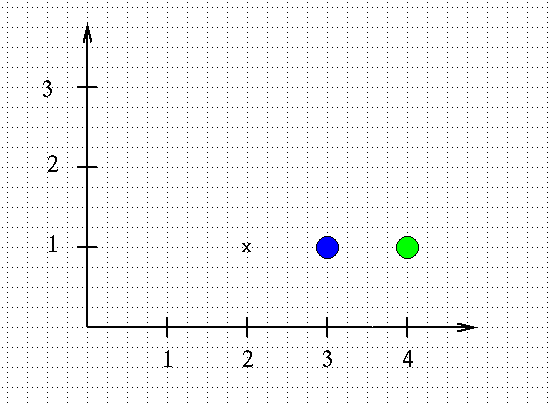
A small metal cross "X" of mass 1 kg is placed at location (2 m, 1 m)

1. What is the gravitational force on the "X" due to the blue ball of mass m = 6 billion kg?
2. What is the gravitational force on the "X" due to the green ball of mass m = 8 billion kg?
3. What is the total gravitational force on the "X"?
4. You have a red ball of mass m = 10 billion kg. Where should you put it to produce a net force of zero on the "X"?

Example 2:

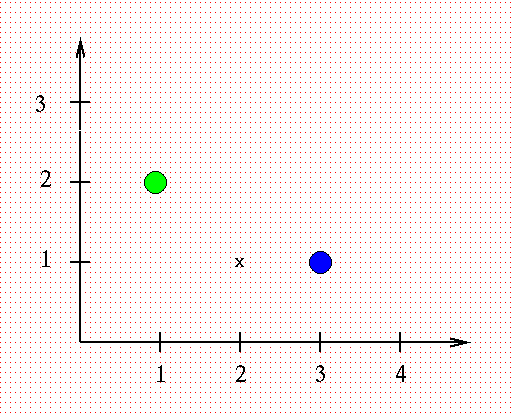
The same small metal cross "X" of mass 1 kg is placed at location (2 m, 1 m)

1. What is the gravitational force on the "X" due to the blue ball of mass m = 6 billion kg?
2. What is the gravitational force on the "X" due to the green ball of mass m = 8 billion kg?
3. What is the total gravitational force on the "X"?
4. You have a red ball of mass m = 10 billion kg. Where should you put it to produce a net force of zero on the "X"?