Determining the friction in Atwood's machine

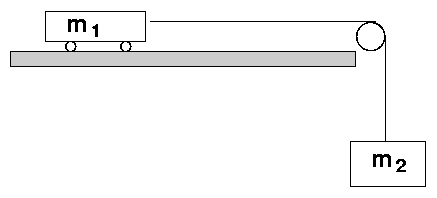
You have seen before this version of a modified Atwood's machine:

If we hold the cart motionless, then release it, it will slide towards the pulley as the weight falls downwards. In the past, we assumed that the cart rolled and the pulley rotated without friction. But in real life, there will be some friction which acts to slow the cart down. Can you figure out the acceleration of the cart -- which is the same as that of the weight -- in the presence of friction?

Let's make free-body diagrams of the cart and the weight separately.

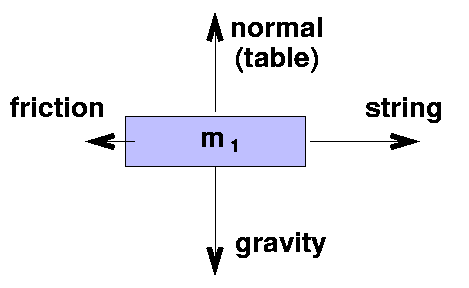
     Force          x          y   
  -----------------------------------
  string           +T           0
  normal (table)    0          +N 
  gravity           0          -m1*g
  friction         -f           0
  -----------------------------------
   total          m1*ax       m1*ay
  -----------------------------------

If we add up the forces in each direction and use Newton's Second Law, we get

    T  -  f     =  m1*ax                                (Eq 1)

    N  -  m1*g  =  m1*ay   =   0   --->   N  =  m1*g     

We want to know ax for the cart, but we still have two unknowns and only one equation. Rats. Let's look at the hanging weight.

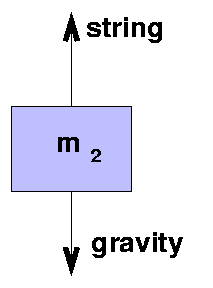
     Force          x          y   
  -----------------------------------
  string            0          +T
  gravity           0        -m2*g
  -----------------------------------
   total          m2*ax       m2*ay
  -----------------------------------

For this object, we find Newton's Second Law says:

    0  -  0     =  m1*ax   =   0

    T  -  m2*g  =  m2*ay                        (Eq 2)

Putting together Eq 1 (from the cart) and Eq 2 (from the weight), we find

    T  -  m2*g  =  m2*ay                        (Eq 2)

    T  -  f     =  m1*ax                        (Eq 1)

Because the two objects are tied together with the same piece of string, the tension T is the same in both. In addition, the magnitude of the two accelerations must be the same. However, note that if the cart goes to the right (in +x direction, so accel ax is positive), then the weight must drop downwards (in -y direction, so accel ay is negative). This means that ax = -ay. Let's replace ay by -ax and solve for the acceleration of the cart.

    T  -  m2*g  =  m2*(-ax)                     (Eq 2)

    T  -  f     =  m1*ax                        (Eq 1)

             (ready?)




           m2 * g           f
   ax  =   -------   -   -------
           m1 + m2       m1 + m2

Is friction significant?

1. 2.3 N +/- 0.1 N
2. 2.3 N +/- 50 N
3. 2.3 N +/- 5 N

How can you tell if the friction in this experiment is signficantly different from zero? Note that the equation for acceleration has two parts: if we keep the total mass (m1 + m2) constant, and just change the hanging weight, then

           m2 * g           f
    a  =   -------   -   -------
           m1 + m2       m1 + m2


         this part      this part
         changes        remains
         with m2        the same

It becomes even more clear if we re-write it like this:

          [   g     ]               f
    a  =  [ ------- ] * m2   -   -------
          [ m1 + m2 ]            m1 + m2

This looks like the equation of a line:

    y  =    (slope)   * x    +   y-intercept

So, if you can measure the acceleration for several different values of hanging mass (while keeping total mass constant), and graph the acceleration versus the hanging mass, you can use the y-intercept to determine the friction ... AND whether it differs from zero.

Doing the experiment

1. Set up a cart on a track, with pulley and hanging weight. Put the force sensor and two mass bars into the cart to make it as massive as possible.
2. Make measurements of the time to slide 50 cm with 5 different values of m2 in the range of 15 to 35 grams
   • try to keep the hanging mass from swinging as it falls
   • remember that m2 will be the mass of the hanger plus any weights attached to it
   • for each mass, make 3 different trials
3. Calculate the acceleration of the cart for each trial; you should have 3 values for each choice of mass m2
4. Make a graph showing all your measurements of acceleration versus the hanging mass. You should probably turn your paper sideways before you start ...
5. Draw a best-fit line, plus lines with min and max estimated slopes. Extend all lines so that they go through and past the y-axis

The most important value you must derive is the size of the friction force, plus its uncertainty. Is it significantly different from zero?

If you have more time ...

1. Use the slope of your line to estimate the value of g, with uncertainties. Does it agree with the usual value?
2. Turn the friction force f you determined into a coefficient of kinetic friction mu.
3. Are there any assumptions made in this analysis which trouble you?

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.