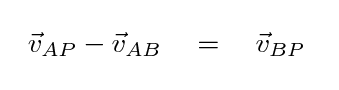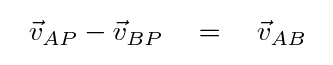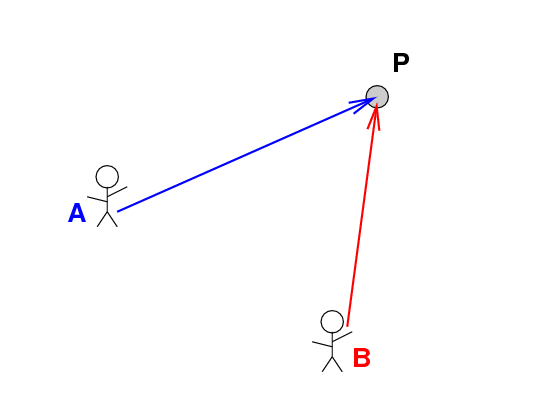
Students A and B measure the position of a hockey puck P. Each student uses her own position as the origin of her coordinate system. They get different results, of course.

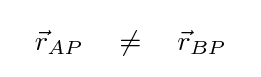
We can figure out the relationship between these two vectors, however, by finding a way to start at A and move first to B, then to the puck.
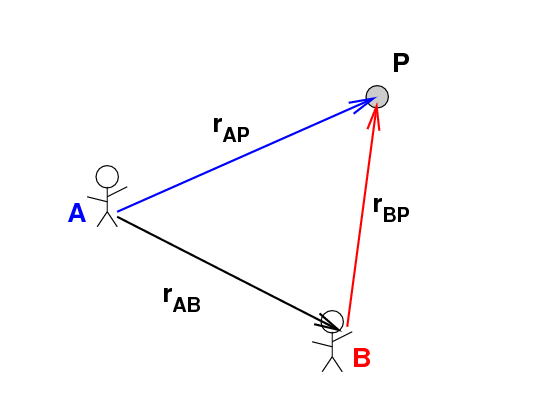
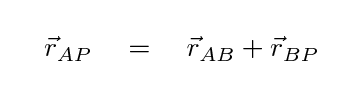
And that means that we can determine the difference between the two vectors from A to the puck and B to the puck. We can use plain old math ....
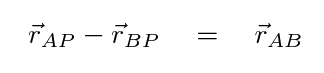
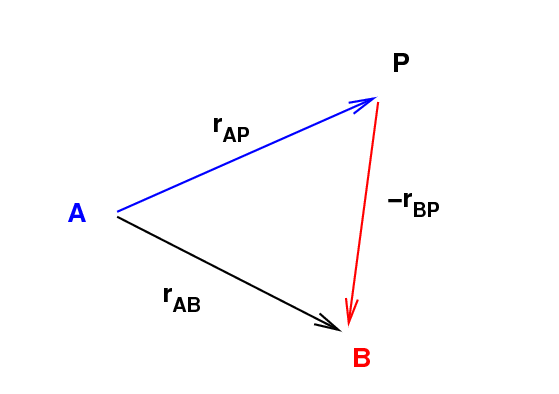
... or we can draw a picture.
We can use the same type of analysis to figure out the velocities measured by one person relative to another. For example, students A and B go outside. Student A stands next to a cannon, while student B rolls to the East on a skateboard.
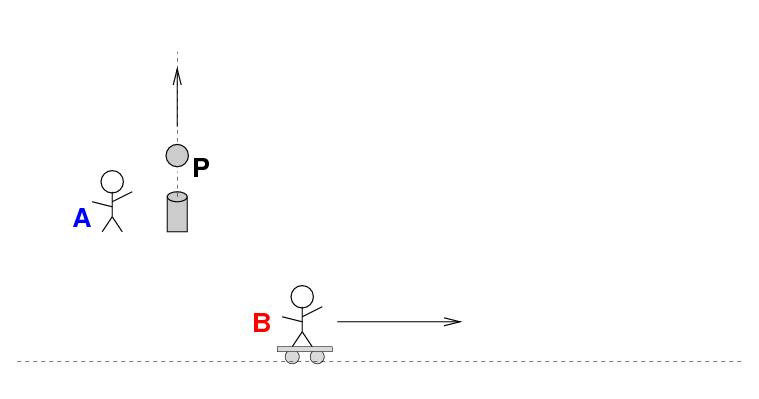
*BOOM* The cannon fires a ball P straight up into the air. Student A measures the velocity of the cannonball P, VPA, and the velocity of the skating student B, VBA.
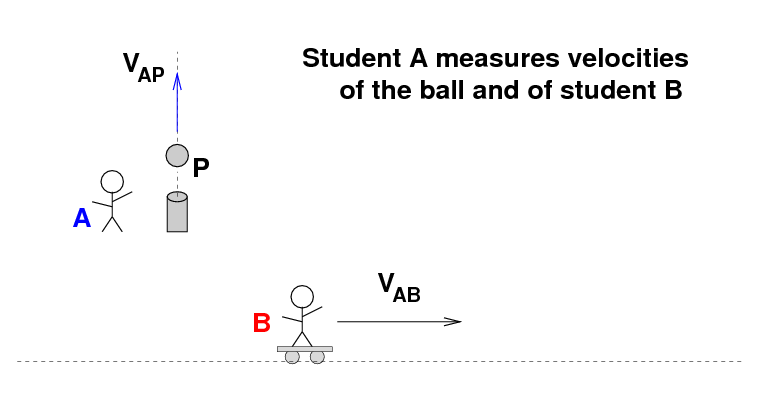
But what about student B? If she measures the velocity of the cannonball, she'll see that it has two components: motion upwards, and motion "backwards" to the West. We can determine the velocity she measures graphically ...
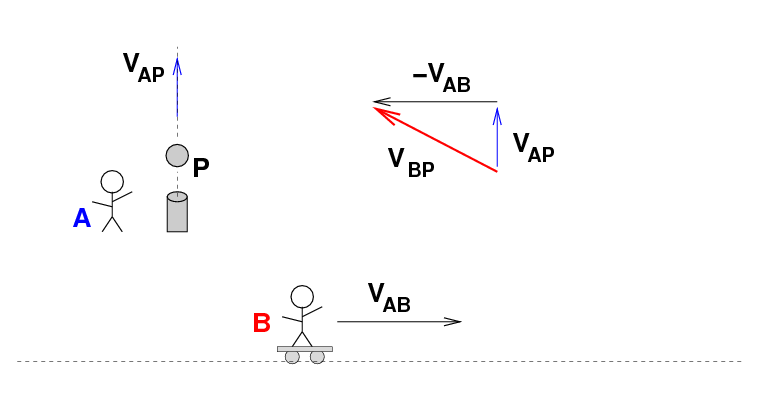
... or using mathematics: