 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
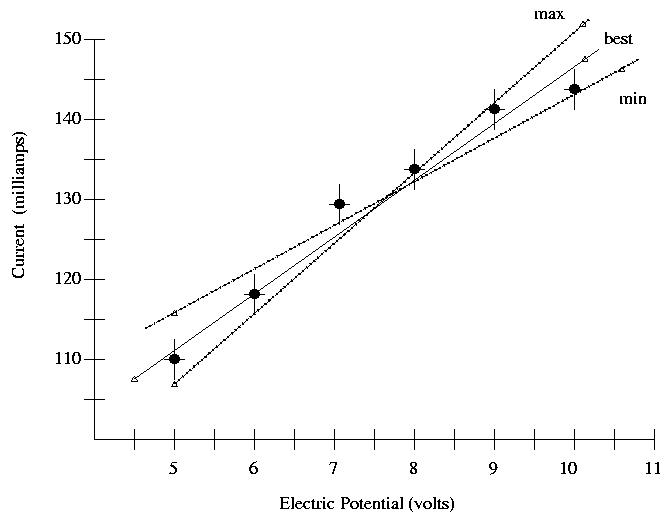
If one has more than a few points on a graph, one should calculate the uncertainty in the slope as follows. In the picture below, the data points are shown by small, filled, black circles; each datum has error bars to indicate the uncertainty in each measurement. It appears that current is measured to +/- 2.5 milliamps, and voltage to about +/- 0.1 volts. The hollow triangles represent points used to calculate slopes. Notice how I picked points near the ends of the lines to calculate the slopes!

In the example above, I find
147 mA - 107 mA mA
"best" slope = ------------------ = 7.27 ----
10 V - 4.5 V V
145 mA - 115 mA mA
"min" slope = ------------------ = 5.45 ----
10.5 V - 5.0 V V
152 mA - 106 mA mA
"max" slope = ------------------ = 9.20 ----
10 V - 5.0 V V
mA
Uncertainty in slope is 0.5 * (9.20 - 5.45) = 1.875 ----
V
There are at most two significant digits in the slope, based on the uncertainty. So, I would say the graph shows
mA
slope = 7.3 +/- 1.9 ----
V
Last modified 7/31/2007 by MWR.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.