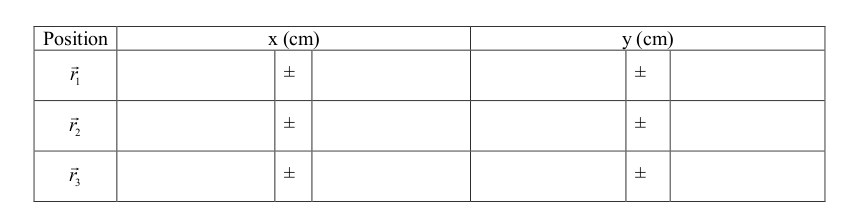
In this activity you will construct real position vectors to various points on your work table and then determine the displacement vectors between these points. Each table will split as evenly as possible into two teams, A and B. Each team will measure the components of three position vectors and determine corresponding displacement vectors.
On your table you will find 3 colored dots labeled 1, 2, 3. These represent the points for which you will find position vectors. In addition there will be two pieces of paper with Coordinate System Origins marked A (for Team A) and B (for Team B.)
Using a meter stick, your team will measure the x- and y-components of the position vectors for each of the three points using the coordinate system origin for your team. Measure as accurately as you can and estimate the uncertainties.

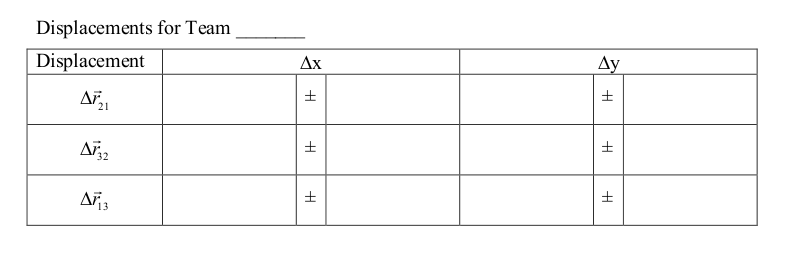
Next, use your position vector measurements, r1, r2, r3 to determine the components of the three displacement vectors Δr21 = r2 - r1, Δr32 = r3 - r2 and Δr13 = r1 - r3. For each component of each displacement, calculate the measurement uncertainty, using the error propagation rules.
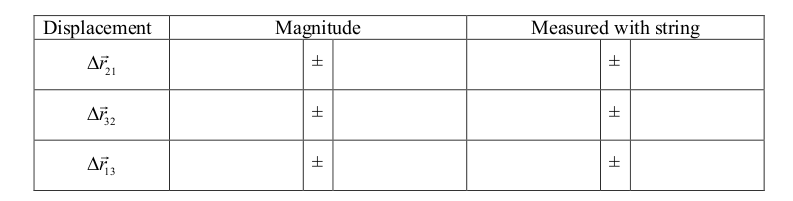
Now calculate the magnitude of the displacement vector between each pair of points and its uncertainty, using the information recorded above, and enter into a table. Finally, you can use a piece of string stretched between the points to determine the magnitude of the displacement and its uncertainty in each case.
Questions: