 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Some 1D kinematics problems
In each problem, figure out first what you know,
what you don't know, and what you WANT to know.
Then pick an appropriate kinematics equation.
Write the equation you are going to use on your
paper before you go on to solve it.
Your textbook derives in Section 2.5 these four equations for the special
(and common) case of constant acceleration:
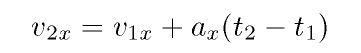
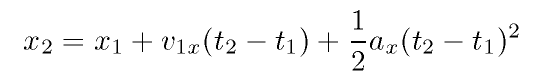
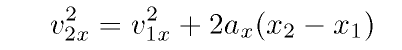
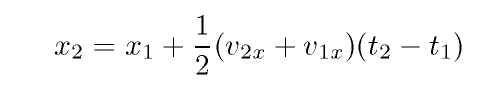
Parts written in italics are optional -- do them only
if you have finished everything else. Beware: they may be
tricky!
- You notice a falcon flying past the Kodak office building
with a constant acceleration.
It goes down 6 stories (each of height 3 meters)
in 1.5 seconds, and at the
end has a downwards velocity of 18 m/s.
Please do remember that falcons have wings....
- What is the acceleration of the bird?
- What was the initial velocity of the bird?
-
You travel to Munchkinland , where
everyone is very short.
The average height of one story is
2 meters.
You watch a falcon fly past an office building there.
Once again, the bird's displacement is
6 stories downwards over the course of 1.5 seconds
at a constant acceleration,
and once again, it ends up with a final velocity
of 18 m/s downwards.
What was the acceleration of this bird?
Draw a picture showing the bird's flight path.
-
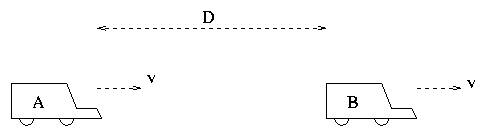
Two automobiles drive in the same direction along
the highway. Each moves initially at speed
55 mph, and the distance between them is D meters.
A deer jumps into the road in front of car B,
and the driver slams on his brakes, so that the car
decelerates at 5 m/s2.
The driver of the following car, A, hesitates for
t = 0.5 seconds, then slams on his own brakes;
car A then decelerates at 3 m/s2.
- How large must the distance D be
for the two cars to avoid a collision?
-
How does the minimum safe distance depend
on the period of hesitation?
Linearly? Quadratically? In some other way?
- Joe stands on the edge of the Grand Canyon. He drops
a rock over the edge, and listens. Eight seconds later,
he hears the faint sound "Plonk".
- How deep is the Canyon?
-
Suppose that Joe repeats his experiment on the Moon:
he drops the rock, then 8 seconds later, feels the vibrations
from the impact in his moon boots.
The speed of sound through the rock is 2300 m/s.
How deep is the lunar canyon?
- Your coop job is with a research group studying ozone depletion.
Your group will launch a rocket that has a mass spectrometer in its
nose cone. You are assigned the task of determining the acceleration
of the rocket so that the equipment can be designed to survive. The
rocket will have has a burn time of t = 30 seconds,
during which time
it flies straight up with constant acceleration a;
call this "Phase I" of the experiment.
After the fuel is exhausted, the
rocket will enter free-fall; call this "Phase II".
You are told that the total time of
flight of the rocket must be T = 300 seconds.
- Draw a graph which shows in schematic form
the height of the rocket versus time.
- Write an equation -- you don't have to know all the values
of the terms -- for the height of the rocket during Phase I.
- Write an equation -- you don't have to know all the values
of the terms -- for the height of the rocket during Phase II.
- Write an equation -- you don't have to know all the values
of the terms -- for the velocity of the rocket during Phase I.
- Write an equation -- you don't have to know all the values
of the terms -- for the velocity of the rocket during Phase II.
- What should you make the acceleration of the
rocket, a, when the engine is on?
- What is the maximum altitude of the rocket?
- Is this problem realistic? Where is the ozone layer anyway?
Look at the answers:
page 1/3
page 2/3
page 3/3
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
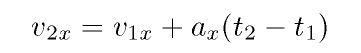
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
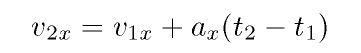
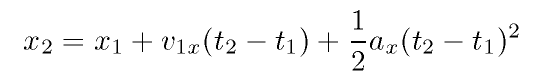
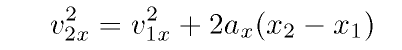
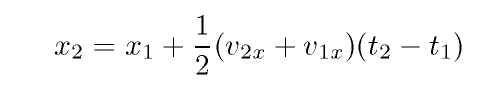

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.