What is the mass of a yardstick?

The goal of this exercise is for your group to predict the mass of a yardstick. If the actual mass lies within your predicted range, you win!

It may sound easy, but here's the problem: you are not allowed to examine or touch the yardstick in question before making the prediction. Instead, you have access to the following:

five pieces of a broken yardstick (which do not add up to an entire yard)
a triple-beam balance scale
a ruler
some graph paper
the knowledge that an intact yardstick is one yard long

To start, please fetch a triple-beam balance scale for your group. Use it to measure the shortest piece of wood in your set. Then have one group member walk up to the board at the front of the room and write down your measurement. We'll talk about using the balance briefly, and discuss the measurements made by each group.

Then, you are on your own. Good luck!

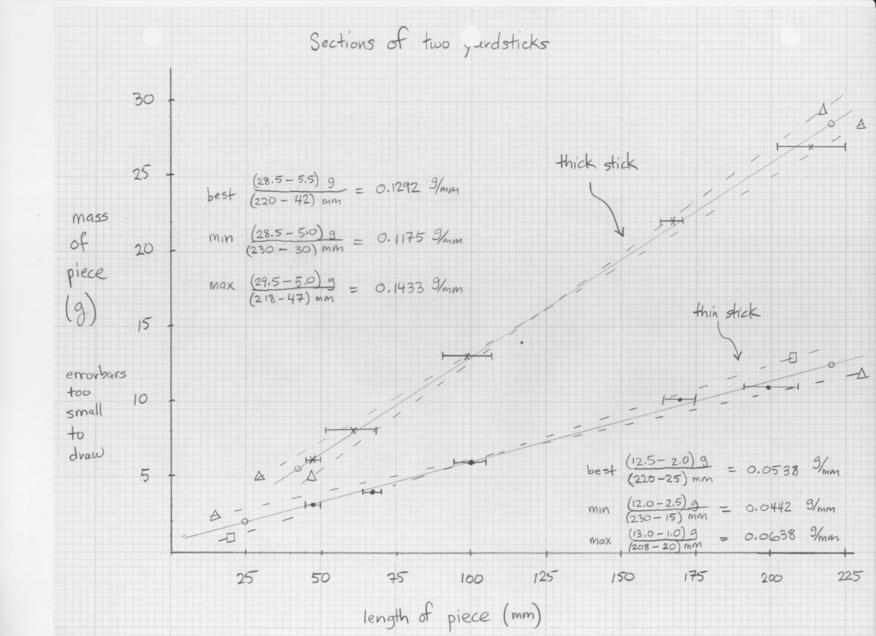
Hint: if you can figure out the linear mass density of a yardstick (that is, the mass per millimeter or centimeter), then you can compute the mass of any given length.

Hint²: if you know the uncertainty in the linear mass density, then you can compute the uncertainty in the mass of any given length.

Hint³: it might help to take a look at the graph below. Click on it to see a larger version.

You must hand in ....

Each group of three students must submit

good graphs, one from each student

plus the following, just one per group:

a neat table of all measurements
a page which shows one example of each type of calculation (but not all the calculations)
the predicted mass (with uncertainty) and actual mass (with uncertainty)
a sentence or two explaining the results -- did the predicted mass agree with the actual mass to within the predicted uncertainty?
your guess at the largest single source of error in the experiment, and how it could be reduced next time