Short-track speed skating
In short-track skating, athletes go around
an oval track which is small enough to fit inside a
regulation hockey rink. The distance around the
inner edge of the oval is L = 111 m.
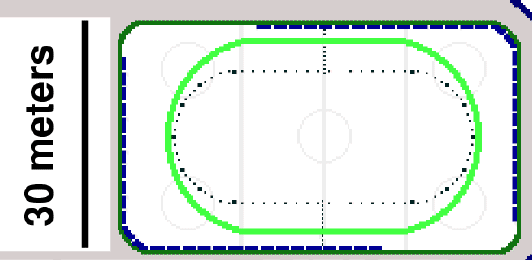
- What is the radius of curvature R of the inner
oval of the track?
The skaters lean way, way over as they speed around
the curves. Although they often place one hand on the
ice for balance, they usually don't press down very
hard on their fingertips.

- Estimate the angle at which these skaters are leaning --
that is, how far above the horizontal is the line
connecting their blades and their center of mass?
Assume that the skaters are at this moment moving
in a circular path with constant speed.
- Draw a free-body diagram showing all forces acting
on a skater. Ignore the fingertip touching the ice.
- Make a table showing the x-component and y-component of each force.
- Figure out the size of the ice's horizontal (= centripetal)
force on the skater. Your answer should have
a factor of m for the mass of the skater.
- Figure out the size of the centripetal acceleration of the skater.
Your answer should NOT have a factor of m any more.
- Based on this analysis, how fast are these skaters moving
in the turn?
- If they kept this same speed for an entire lap,
how long would one lap take?
- The best male skaters can complete a lap in a bit
more than 9 seconds. Does this agree with your
estimate? If not, does it still make sense?
For more information


