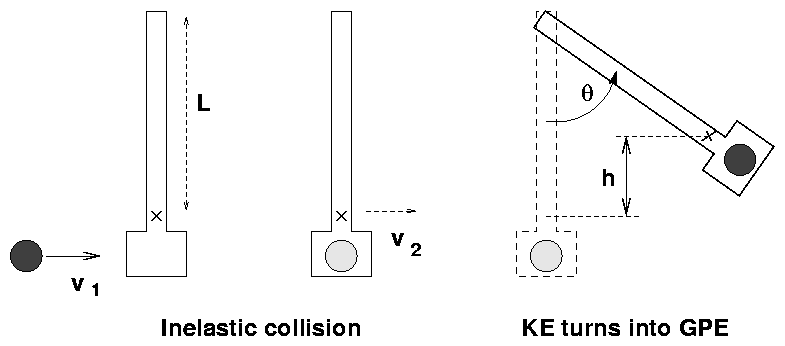
You can break the action into two pieces:
- A ball of mass m moving at speed v1 slams
into an arm of mass M. Use conservation of
momentum in this completely inelastic collision
to write an equation relating v1 to the velocity
of the arm-plus-ball v2.
- An arm with an initial speed swings up until it halts
at an angle theta.
Use conservation of energy to figure out the relationship
between the speed of the arm-plus-ball v2,
the angle theta,
and the height h by which the center of mass of
arm-plus-ball rises.
Your first job today is to figure out the speed v1 with which the
ball is fired from the catapult, by measuring the angle theta
(and some other quantities).
- be very gentle with the swinging arm
- use the stuffing rods to push the ball into the catapult
- make 3 measurements for the "medium-range" setting
of the spring-loaded gun
- you will need to find the position of the center of mass
of the arm-plus-ball
- watch the device when you fire the catapult. If it slides
across the table, your measurements will be inaccurate:
some of the momentum goes into the motion of the whole
device, which you cannot measure
- try to estimate the uncertainty in each of the four
quantities you need to measure
You should end up with one table showing
all your measurements,
and the uncertainty associated with
each measurement.
You should also have a value of
v1,
the velocity of the ball when it leaves
the muzzle of the gun.
Bonus!
Compute the uncertainty in v1.
Your second job is to calculate the spring constant k
of the spring in the gun.
-
Use your measurements of the initial speed
of the ball to compute the kinetic energy
of the ball.
Assume that this kinetic energy (KE) is exactly the
same as the spring potential energy (SPE) stored
in the compressed spring.
Measure the distance -- and uncertainty --
by which the spring is compressed.
Compute the spring constant.
Bonus:
Compute the uncertainty in your value of the
spring constant, using uncertainty in KE and
uncertainty in distance compressed.

