Complicated collisions: the ballistic pendulum (I)

In real life, collisions are often messy affairs which require a mixture of techniques to understand. As an example, consider the ballistic pendulum.

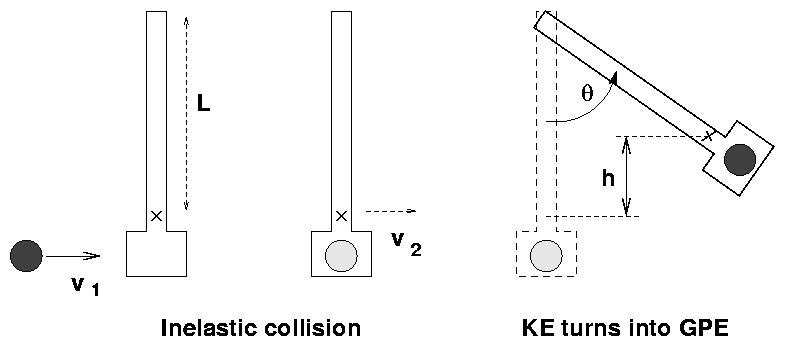
You can break the action into two pieces. Please write an equation for each piece:

1. A ball of mass m moving at speed v1 slams into an arm of mass M. Use conservation of momentum in this completely inelastic collision to write an equation relating v1 to the velocity of the arm-plus-ball v2.
2. An arm with an initial speed swings up until it halts at an angle theta. Use conservation of energy to figure out the relationship between the speed of the arm-plus-ball v2, the angle theta, and the height h by which the center of mass of arm-plus-ball rises.

Your first job today is to figure out the speed v1 with which the ball is fired from the catapult, by measuring the angle theta (and some other quantities).

• record the ID number on your pendulum apparatus, so that you can use it again on Wednesday
• be very gentle with the swinging arm
• use the stuffing rods to push the ball into the catapult
• make 3 measurements for the "medium-range" setting of the spring-loaded gun
• make 3 measurements for the "long-range" setting of the spring-loaded gun
• you will need to find the position of the center of mass of the arm-plus-ball
• watch the device when you fire the catapult. If it slides across the table, your measurements will be inaccurate: some of the momentum goes into the motion of the whole device, which you cannot measure
• try to estimate the uncertainty in each of the four quantities you need to measure

3. You should end up with one table showing all your measurements, and the uncertainty associated with each measurement.
4. Which measurement has the largest percentage uncertainty? If you want to improve this experiment, you should concentrate on doing this part of it more precisely.

Now, show step-by-step how to use your measurements to compute the value of v1, the velocity of the ball when it leaves the muzzle of the gun. What is this velocity

5. for the medium-range setting?
6. for the long-range setting?

Compute the uncertainty in v1, using the rules for propagating uncertainties. What is the uncertainty in the velocity

7. for the medium-range setting?
8. for the long-range setting?

As you try to convert the uncertainties in the values you measured in class into an uncertainty in the initial speed v1 of the ball, you may find it useful to peruse

• this GENERAL guide to using uncertainties in calculations
• this SPECIFIC example of using uncertainties in the ballistic pendulum; the numbers will be different than yours, but the method should be the same
  • Part 1 of example
  • Part 2 of example
  • Part 3 of example

Your second job is to calculate the spring constant k of the spring in the gun. Let's use an energy-based measurement:

9. Use your measurements of the initial speed of the ball to compute the kinetic energy of the ball. Assume that this kinetic energy (KE) is exactly the same as the spring potential energy (SPE) stored in the compressed spring.
10. Measure the distance by which the spring is compressed for the medium-range and long-rang settings. Include an uncertainty with each distance.
11. Compute the spring constant using data from the
    1. medium-range setting
    2. long-range setting
12. Compute an uncertainty in the spring constant for the
    1. medium-range setting
    2. long-range setting
13. The spring constants you computed SHOULD agree within their uncertainties. Do they?