Measuring the acceleration of a cart quantitatively

Once again, you'll send a cart sliding up and down a ramp; but this time, you'll make quantitative measurements of the position and velocity the cart as it goes. You have three main tasks:

find the acceleration as the cart goes UP the ramp
find the acceleration as the cart goes DOWN the ramp
determine if the two accelerations are the same to within the uncertainties

There are some extra jobs for you to do if you manage to finish these major ones.

Setting up

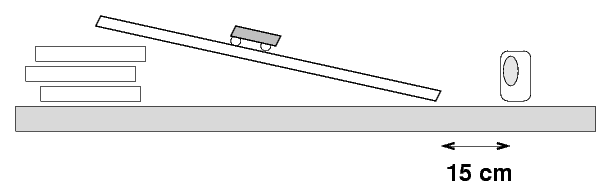
Arrange a ramp to lean at about theta = 4.5 degrees from the horizontal. Fix a white plastic "flag" into a cart and place it on the track. Practice gently pushing the cart upwards so that it slides about two-thirds of the way up the track, stops, then slides back down.

Set up the laptop computer in your drawer. Turn it on and log in using your DCE account name. Take the "LabPro" interface unit, and its power supply, out of the laptop case. Use the USB cord in the laptop case to connect the LabPro unit to the computer.

When you have logged into the computer, open the folder

   My Computer
      Student Shares on 'svphy01' (S:)
         University Physics Students
            Team Physics 311
                Lab Pro

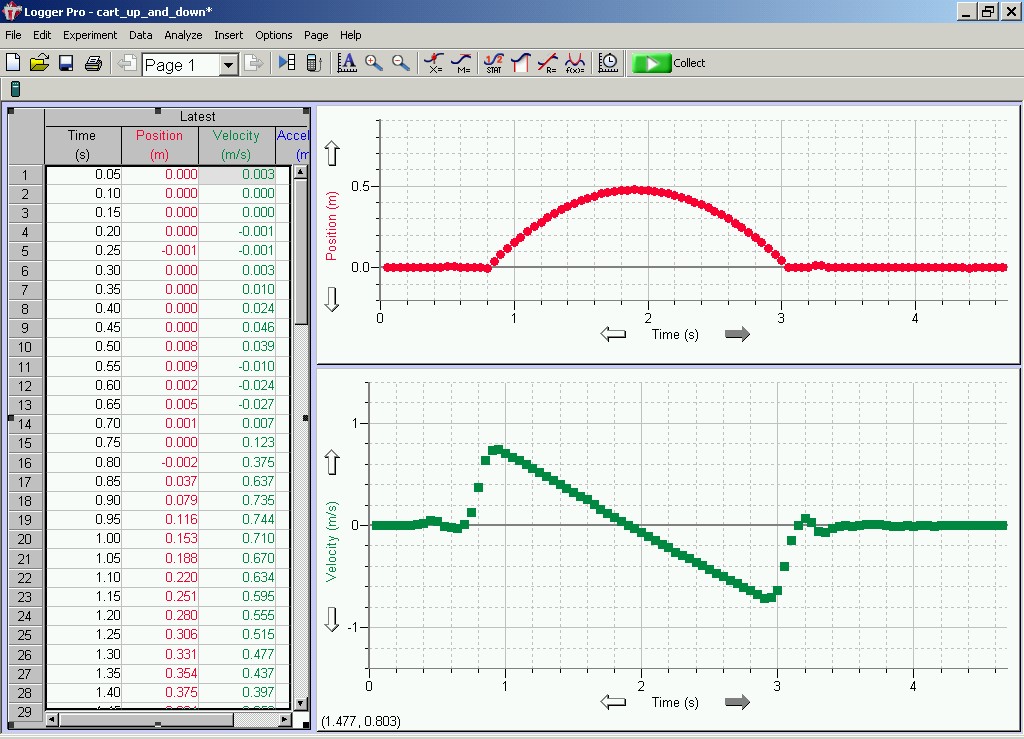
Drag the item cart_up_and_down from the "LabPro" folder to the desktop. Double-click on the copy on the desktop. You should see a screen sor of like this, but without the data points:

Making the measurements

When you click on the Collect button at the top of the screen, the motion sensor will start taking 5 seconds of measurements -- you'll hear it clicking as it works. Practice the following:

start with cart at bottom of ramp
start collecting data
wait a moment, then gently push the cart up the ramp
let it slide up and then back down
catch the cart at the bottom before it rolls off the ramp

until you manage to acquire a "good" set of data. "Good" data will look like that in the example screen above: the position versus time will make a nice parabolic curve, and the velocity versus time will have a roughly linear section. There should be short segments of data before the cart starts to move and after the cart stops moving. Ideally, you'll have about 1 second of "cart going up" and another 1 second of "cart going down".

When you think you have a set of "good" measurements, ask an instructor to verify that they are fine. If you can't succeed, ask an instructor for help.

Analysis

First, figure out three special times:

when the cart starts sliding freely (after your hand releases it)
when the cart reaches the peak of its travel
when the cart stops sliding freely (because you catch it)

Use your times to split the motion into two segments:

when the cart is moving freely up the ramp
when the cart is moving freely down the ramp

You can use the LoggerPro program to figure out the change in velocity with respect to time during each of these two segments. Click-and-drag on the velocity vs. time graph window to highlight data in the first segment; then click on the "Linear Fit" icon near the top of the screen. The program will draw the best-fit straight line to the highlighted data and show you the equation of this line.

What is the acceleration of the cart as it moves up the ramp? What is the acceleration of the cart as it moves down the ramp? Use the File -> Print Graph feature to print out onto paper a copy of your data with the linear fits.

Now, the real question is -- are these accelerations the same? LoggerPro will not tell you about the uncertainty in its fits to the data, unfortunately, so you'll have to do this yourself.

pick roughly 10 measurements during each time segment (10 going up, 10 going down)
make a table showing these 20 measurements
make one graph for each time segment, showing velocity on the vertical axis and time on the horizontal axis
draw two lines on each graph: one showing the "min" slope which seems consistent with at least some of the data, and another showing the "max" slope
calculate the slope of each line

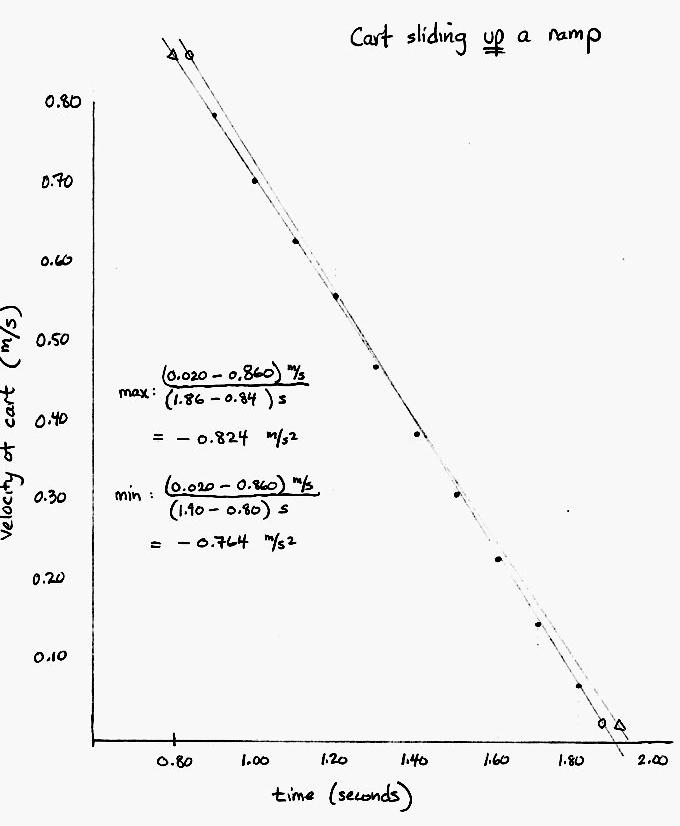
You can use these graphs to estimate the uncertainty in the acceleration during each time segment.

Is the acceleration of the cart while it slides up the ramp EXACTLY equal to that of the cart while it slides down the ramp? Are they the same to within the uncertainty? If the two accelerations are NOT equal, explain why not. Use both text and pictures in your explanation.

If you have time ....

Do as many of the following as time permits.

How do your min and max accelerations compare to the best-fit accelerations determined by LoggerPro?
What was the DIRECTION of velocity and acceleration while the cart was going up the ramp?
What was the DIRECTION of velocity and acceleration while the cart was at the very top of its motion?
What was the DIRECTION of velocity and acceleration while the cart was going down the ramp?
What was the velocity of the cart when your hand released it?
Calculate the average acceleration of the cart. Assuming that the acceleration of the cart was constant and had this value, write an equation which gives the velocity of the cart as a function of time-after-release.
Using this equation with average acceleration, determine when the cart should have stopped moving. How close is it to the time that the cart actually stopped moving?
Again assuming that the acceleration was constant, with the average value, write an equation which gives the position of the cart as a function of time-after-release.
Using this equation, where should the cart have been exactly 1.2 seconds after you released it? How close it that to the actual position of the cart at 1.2 seconds after release?
Using LoggerPro, fit the graph of position versus time with a quadratic function. Write down the parameters of this function, including the units of each one. How does this function compare to your equation for position as a function of time?
In theory, the acceleration of a cart rolling freely along a ramp tilted at angle theta should have magnitude g sin(theta). Is this equal to your measured acceleration(s) within the experimental uncertainty? If not, try to explain any difference.