The leaning ladder

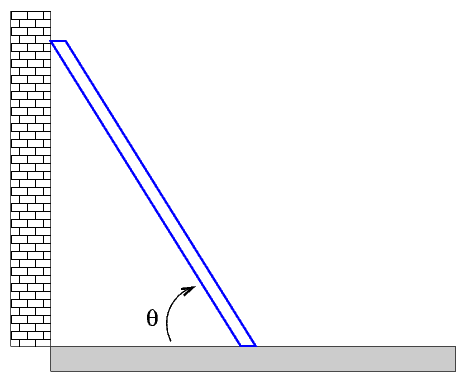
A ladder of length L and mass M leans up against a wall at an angle theta from the horizontal.

The top end of the ladder has been polished smooth, so there is no friction between the top end and the wall. The bottom end of the ladder, on the other hand, scrapes against the ground with a coefficient of static friction mu.

What is the critical angle theta below which the ladder will slide away from the wall and fall down?

In order to answer this question, you might try

1. Identifying all the forces acting on the ladder
2. Identifying all the torques acting on the ladder (hint: pick the bottom of the ladder as the pivot point)
3. Making a table with columns for forces in X, forces in Y, and torque
4. Finding the conditions under which the sum of forces in each direction is zero, and the sum of torques in each direction is zero

Suppose that the ladder has length L = 5 m and mass M = 8 kg, and the coefficient of static friction is mu = 0.20. What is the critical angle?

Extra: Painter Mario has a mass M = 50 kg. He takes two steps up onto the ladder, moving a distance d = 1 m along the ladder away from the ground. Does the critical angle remain the same, increase, or decrease? In fact, what is the critical angle now?

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.