Distance between two locations on the Earth

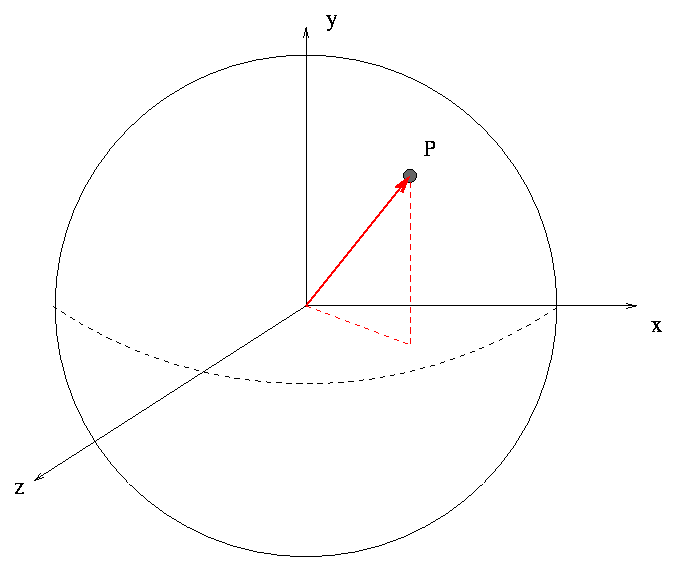
We often describe a location on Earth by its latitude and longitude. How are these related to the Cartesian xyz coordinates of the location (relative to the center of the Earth)? In the diagram above, imagine that the point at which longitude equals zero is located in the direction of the x-axis.

Draw in the angle which corresponds to longitude.  Call it "a".

Draw in the angle which corresponds to latitude.   Call it "b".


What is the x-component of vector P?

What is the y-component of vector P?

What is the z-component of vector P?

Now, try to use this information to determine the distance between two cities:

Rochester, NY, is at longitude 77.60 W, latitude 43.16 N.
Rochester, MN, is at longitude 92.47 W, latitude 44.02 N.

What is the distance between the two Rochesters? One can answer this two ways:

the distance along the Earth's surface, as one would drive a car
the straight-line distance through a tunnel connecting the two cities

Try to calculate the second distance. It's not too hard if you can write down the components of the vectors running from the center of the Earth to each city:

Rochester, NY      x =                y =                z =

Rochester, MN      x =                y =                z =

--------------------------------------------------------------------------
displacement       x =                y =                z =


Magnitude of displacement =               km

Can you figure out the distance between the two cities along the Earth's surface? (Hint: it may help to use the dot product to find the angle between the vectors for the two cities)