 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Work by Variable Force, and Spring Force
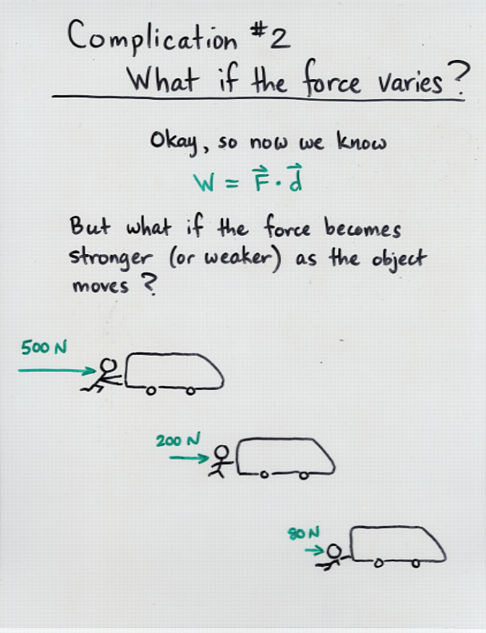
- When a force varies as it pushes or pulls an object,
one cannot simply calculate work as the product
work = (force) * (distance)
Instead, one must integrate the force through the distance
over which it acts
/
work = | (force) * (dx)
/
As before, if the force and displacement are not in exactly
the same direction, one must take the dot product within
the integral.
- Springs are very important because they serve as simple
models for lots of complicated physical systems.
Objects which behave like springs behave in a manner which
is described as simple harmonic motion;
you will see SHM over and over as you continue in physics.
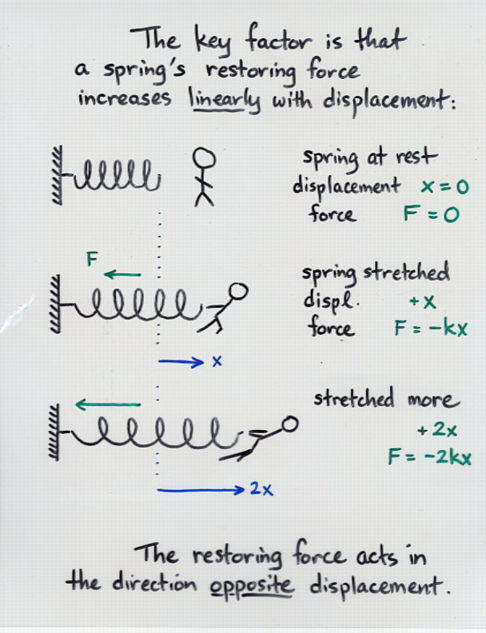
- The defining character of a spring is that it resists
displacement from its rest position with a force which
increases linearly:
restoring force = - k * (displacement)
where k is called the spring constant.
It has units of Newtons per meter.
- When a spring pulls something, or pushes something, over
a distance x, it does work
2
work = 1/2 * k * x
- If a spring is compressed (or stretched) it stores energy
equal to the work performed to compress (or stretch) it.
We might call this spring potential energy.
Viewgraphs
 Viewgraph 1
Viewgraph 1
 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
 Viewgraph 4
Viewgraph 4
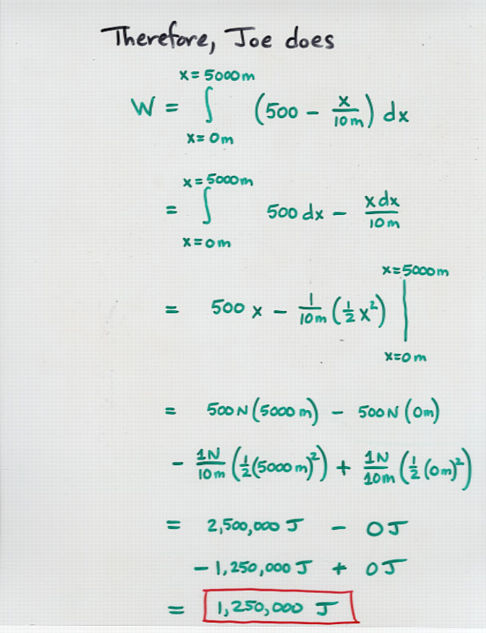 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
 Viewgraph 7
Viewgraph 7
 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
 Viewgraph 10
Viewgraph 10
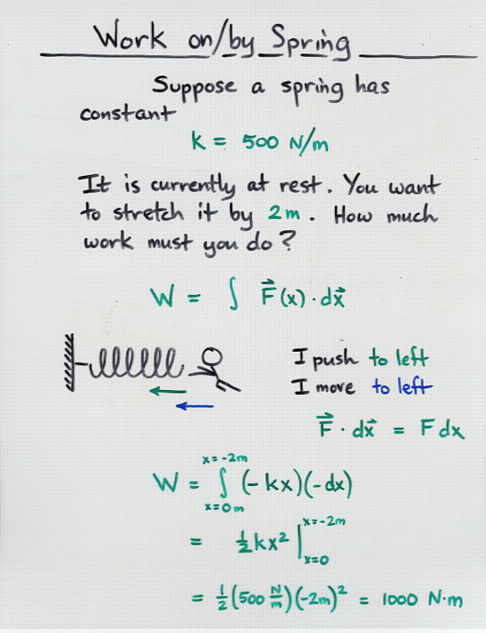 Viewgraph 11
Viewgraph 11
 Viewgraph 12
Viewgraph 12
 Viewgraph 13
Viewgraph 13
 Viewgraph 14
Viewgraph 14
 Viewgraph 15
Viewgraph 15
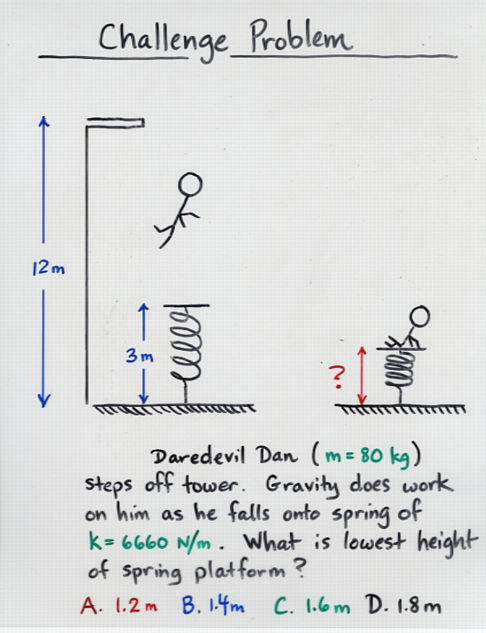 Viewgraph 16
Viewgraph 16
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
 Viewgraph 1
Viewgraph 1
 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
 Viewgraph 4
Viewgraph 4
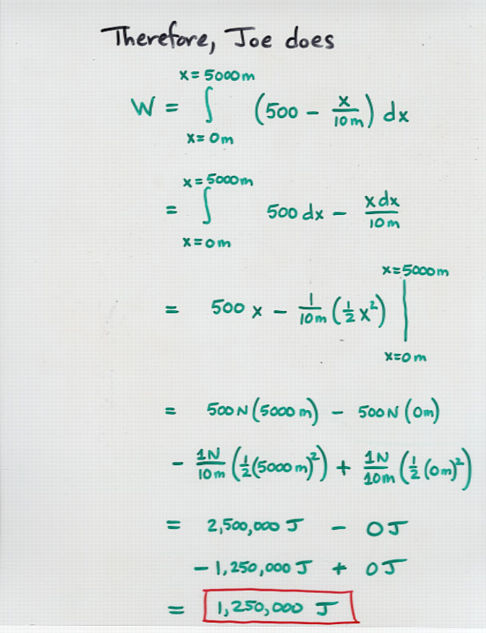 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
 Viewgraph 7
Viewgraph 7
 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
 Viewgraph 10
Viewgraph 10
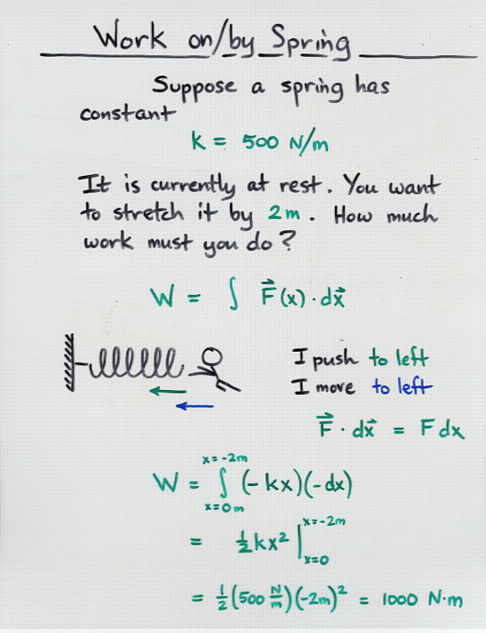 Viewgraph 11
Viewgraph 11
 Viewgraph 12
Viewgraph 12
 Viewgraph 13
Viewgraph 13
 Viewgraph 14
Viewgraph 14
 Viewgraph 15
Viewgraph 15
 Viewgraph 16
Viewgraph 16
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.