Force, Momentum, and Impulse

Force, Momentum, and Impulse

We know how to calculate the kinetic energy of moving objects -- isn't that enough? No. It turns out that many situations involving collisions do not obey the simple conservation of Mechanical Energy. Why not? Because it takes energy to bend, break, mutilate and deform objects, energy which disappears from the kinetic and gravitational potential energy.
But a different quantity is conserved, even during collisions. The linear momentum of an object is defined as
```
                   p  =  (mass) * (velocity)
```
It is a vector quantity, and the total linear momentum of a bunch of objects will remain the same, before and after a collision.
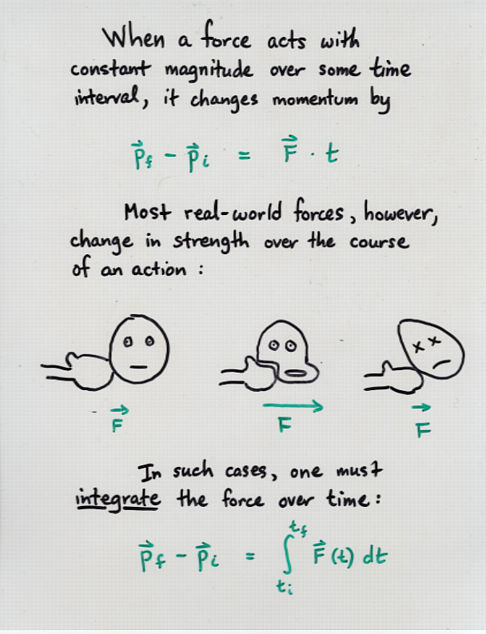
Momentum is connected to force by impulse, which is simply
```
            impulse   =  (force) * (time)
```
if the force has a constant magnitude during its action. If the force changes with time, then one must integrate to find the impulse:
```
                         / 
            impulse   =  |  (force) dt
                         /
```

The Momentum-Impulse Theorem states that the change in momentum of an object is equal to the impulse exerted on it:

           (change in momentum)    =  (impulse)

             p      -   p          =  (force) * (time)
              final      initial
     
           m*v      -  m*v         =  (force) * (time)
              final       initial

Viewgraph 1

Viewgraph 2

Viewgraph 3

Viewgraph 4

Viewgraph 5

Viewgraph 6

Viewgraph 7

Viewgraph 8

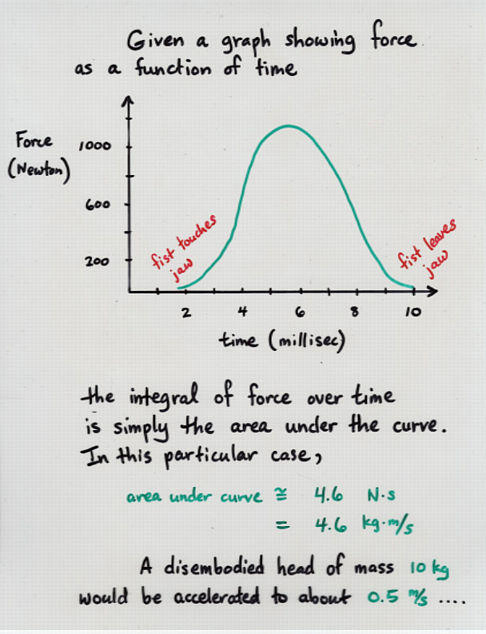Viewgraph 9

Viewgraph 10