![]()
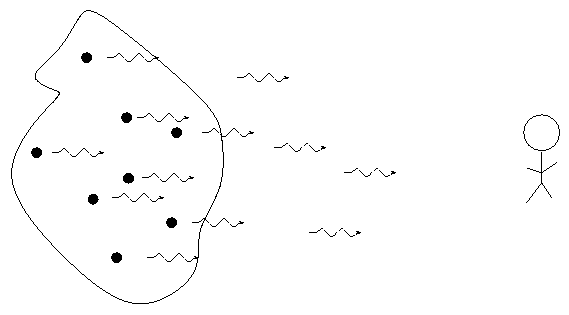
![]()
![]()
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
By a very fortunate circumstance, it turns out that we can figure out the composition of many celestial bodies, even though they are much, much too far away for us to sample directly. How? Through the properties of light.
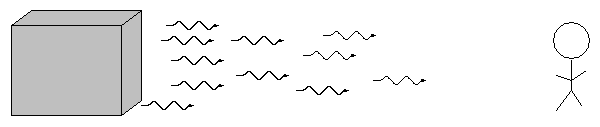
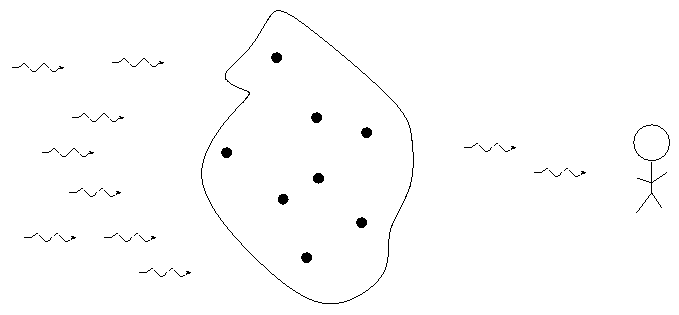
It turns out that each element has a characteristic "signature" in the way it emits or absorbs light (and other forms of electromagnetic radiation). In order to see these signatures, we need to break light up into its constituent wavelengths. We can do this with a prism, or with a grating; either way, the result is a spectrum.
The type of spectrum we see depends on the nature of the source.

![]()
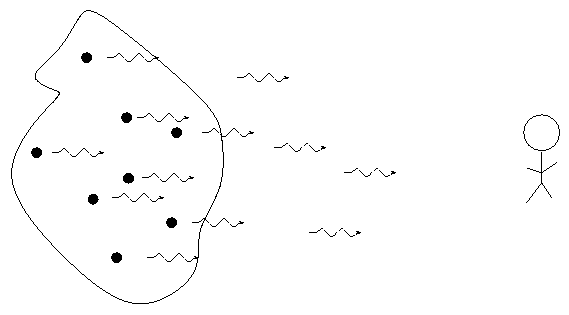
![]()

![]()
Each element (and ionization state) generates its own unique set of wavelengths of emission or absorption. For example, compare spectra of hydrogen:
![]()
helium:
![]()
and carbon:
![]()
Spectra can tell us more about an object than its composition -- they can also reveal one component of the object's motion, through an effect called the Doppler shift.
When an object is neither moving towards us nor away from us, it emits light at exactly the same wavelengths we see in labs on Earth. For example, a cloud of hydrogen (H) emits light with wavelengths of 6563 Angstroms and 4861 Angstroms.
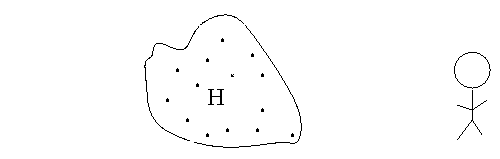
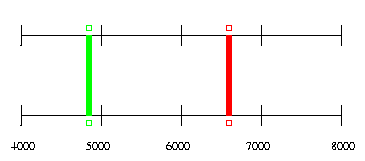
If the cloud moves away from us with some speed v, then it still emits light at the same wavelengths, which we call the "rest wavelengths"; but we perceive that light to have shifted to the red by an amount
( v )
new wavelength = (rest wavelength) * ( 1 + --- )
( c )
This formula is accurate for speeds much less than the
speed of light; at relativistic speeds, one must include
more complex terms.
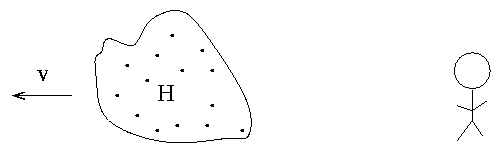
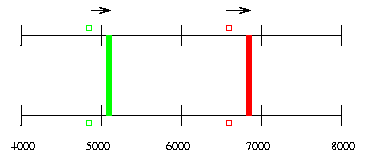
If the cloud moves towards us with some speed v, then it still emits light at the rest wavelengths ... but we perceive that light to have shifted to the blue by an amount
( v )
new wavelength = (rest wavelength) * ( 1 - --- )
( c )
Again, this formula is accurate only for speeds much less than the
speed of light.
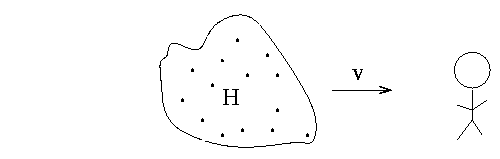
If an object is rotating, then different parts of it may appear to have different radial velocities.

The portions of the object which is moving towards the observer will be blue-shifted, and the portions moving away red-shifted. Most of the area moves nearly across the observer's line of sight, and so shows little or no shift. The result is a spectral feature which shows blue and red wings; the width of the feature can be used to estimate the speed of rotation.
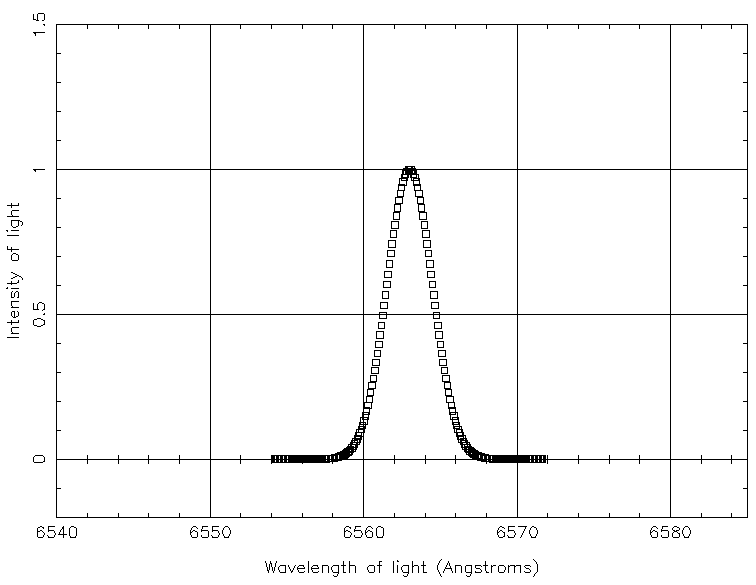
In the example above, a hydrogen gas cloud emits light at a rest wavelength of 6563 Angstroms. How fast is it rotating?
Further information:
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.