
Image from experiments done in Physics 492 at California State University, LA
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
How do we measure the size of a room? That's easy: bring a tape measure into it, stretch the tape measure across the floor, and voila!
How do we measure the size of a star? That's hard: we can't walk up to a star and stretch a tape measure from one side to the other. But don't give up: with a little help from trigonometry and physics, we can still get pretty good estimates for the size of many stars.
It turns out that there are several different methods for measuring the size of a star.
As we discuss each of the methods below, keep in your mind a single, concrete example: could this method determine the size of an ordinary star like the Sun, if it happened to be a mere 10 parsecs away from us?
Q: What is the angular size of a sun-like
star at a distance of 10 pc?
Express your answer in degrees,
arcseconds, and milli-arcseconds (mas).
It seems obvious: if you want to measure the size of a star, just point your telescope at it and take a picture. Measure the angular size of the star in the image, then use the distance to find the true linear diameter. What's so hard about that?
Well, for one thing, images taken from the Earth's surface are blurred by motions in the Earth's atmosphere. We can't see details much smaller than 1 arcsecond in size, so no star but the Sun appears as more than a blob in ordinary optical ground-based pictures.
But what about telescopes in space? Since they don't have to look through the Earth's atmosphere, can't they take pictures sharp enough to resolve stars into little disks of light? Alas, no.
The problem is a phenomenon called diffraction.
If you use a real optical system with an aperture of diameter D,
light rays won't come to a perfect point at the focus;
instead, interference from rays entering the aperture at different
locations will form a fuzzy blob of light, surrounded by a series
of faint rings.

Image from experiments done in
Physics 492 at California State University, LA
This pattern is called the "Airy pattern" after George Airy, Astronomer Royal of England, who first derived the angular size of the central blob and the rings which surround it. The intensity and spacing of the rings are related to the Bessell function of first order, J1. For our purposes, the important item is the angular size of the central blob, from its center to the first minimum in the diffraction pattern.
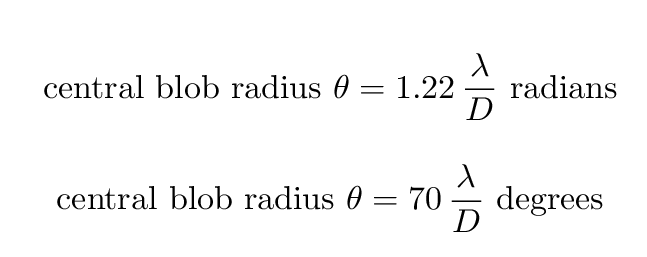
Q: In order to resolve a sun-like star at 10 pc,
using pictures in visible light (550 nm),
how large would a telescope's aperture have
to be? Remember that
10 pc = 3 x 10^(17) m.
solar radius = 7 x 10^8 m
It helps to work as far into the ultraviolet as possible, since the decrease in wavelength λ shrinks the Airy pattern. Unfortunately, the Earth's atmosphere prevents ultraviolet light from reaching the ground. Astronomers have used telescopes in space to take near-UV images of a very few stars in hopes of resolving them.
In at least one case, they have succeeded -- barely, and only because this star, Betelgeuse, is much, much, MUCH larger than the Sun. Here's an image from the press release:

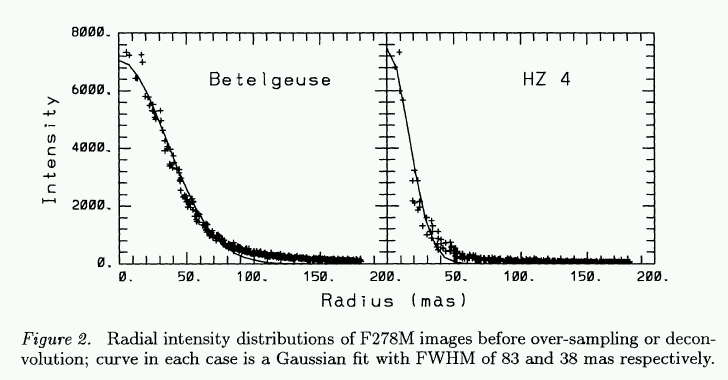
And here are a pair of radial profiles, of Betelgeuse and an unresolved star, from a conference proceeding describing the observations.
Q: The parallax of Betelgeuse is 0.00764 arcsec.
What is the diameter of Betelgeuse? Express
your answers in terms of the solar diameter.
So, the simplest approach to measuring the size of a star -- just take a picture -- works only for a very few stars, and only with ultraviolet images taken by the HST. How else can we measure sizes?
The basic idea is simple:
Sounds easy, right? Just watch as the moon's limb covers the star:
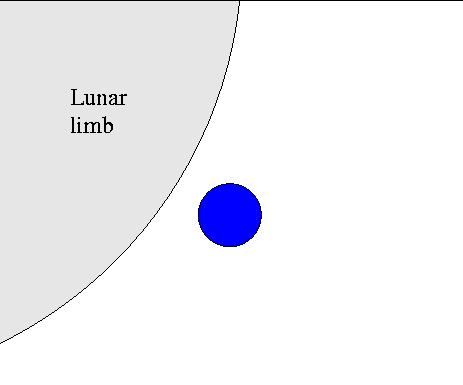
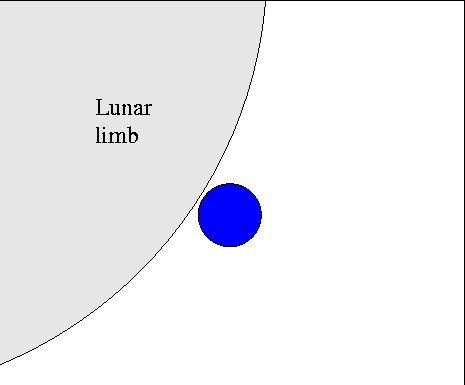
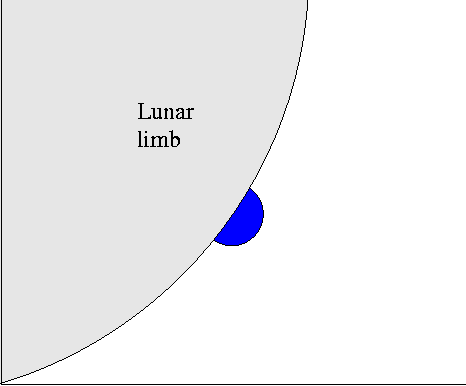
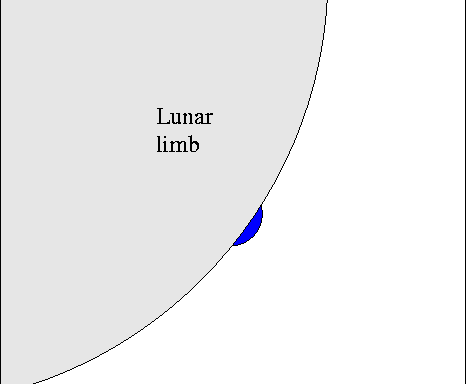
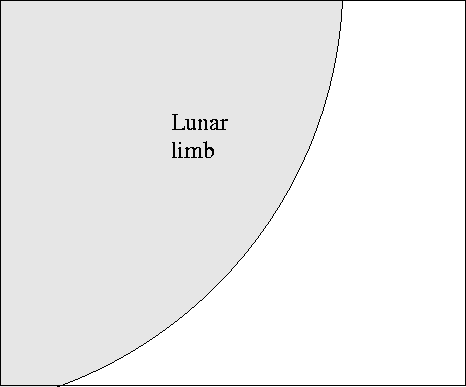
The time it takes for the star's light to disappear, Δt,

is just the angular size of the star θ divided by the angular speed v of the Moon through the sky.
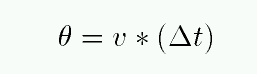
Q: What is the Moon's angular speed through the sky?
Express your answer in arcseconds per second.
Q: How long would it take for the Moon's limb to
cover a star of angular diameter 100 mas?
Uh-oh. It appears that any lunar occultation will be a very quick event. One will need
This requirement of collecting lots of photons in a very short time is a killer. The lunar occultation method is therefore restricted to relatively bright stars. It's also restricted to stars which happen to lie near the ecliptic, of course.
But ... it's even worse! It turns out that diffraction makes life difficult for astronomers again. As the Moon's limb begins to pass in front of the star's disk, it diffracts the light from the star. As an analogy, you know the diffraction pattern of light passing through a narrow slit.
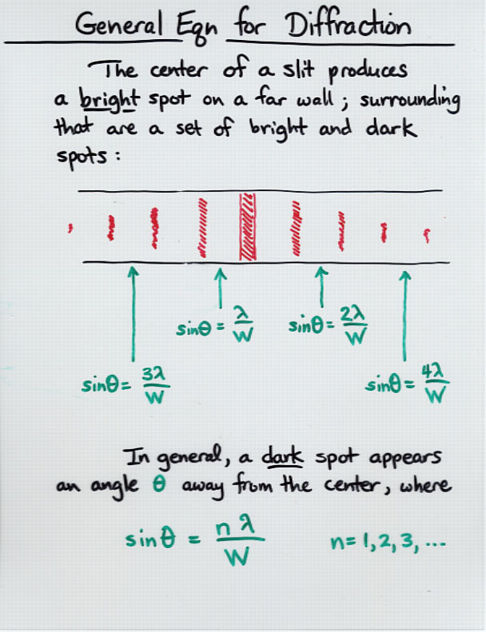
As the Moon's limb approaches and covers a star, we on the Earth see something like this pattern of alternating dark and light spots moving past our detectors. So the light curves (intensity versus time) that we record will be somewhat more complicated than the simple decreasing curve shown earlier.
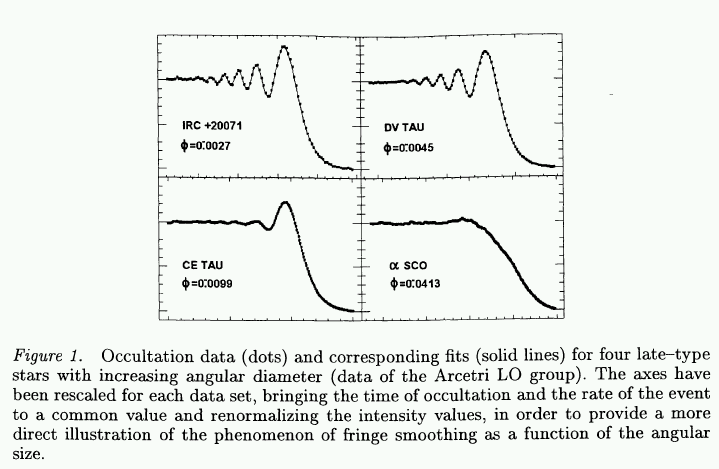
Figure from
White (1998)
The mathematical analysis of these real light curves is a complicated business. Once again, Bessel functions come into play. One must also make some assumptions about the star itself: is it a uniformly bright disk with a sharp edge, or is it limb-darkened like the Sun?
The bottom line is that the lunar occultation method is effective at measuring the angular diameters of stars down to about 1 mas. Back in 1987, White and Feierman published a catalog angular diameters of 124 stars measured by lunar occultations. A paper by Richichi states that another 50 stars were measured in this way up to 1998. The lunar occultation method has very clear limits, but clearly has given us a great deal of information on stellar sizes.
Fortunately, the Moon isn't the only "moving knife edge" we can use to determine the sizes of stars. There are many instances in which we can use one star as the "moving knife edge" to measure the size of a second star. All we have to do is find an eclipsing binary system: a pair of stars orbiting around each other, oriented in space so that one star passes in front of the other as seen from the Earth. If we measure the light coming from such a system carefully, we can detect the decrease in total intensity as a portion of one of the stars is covered:
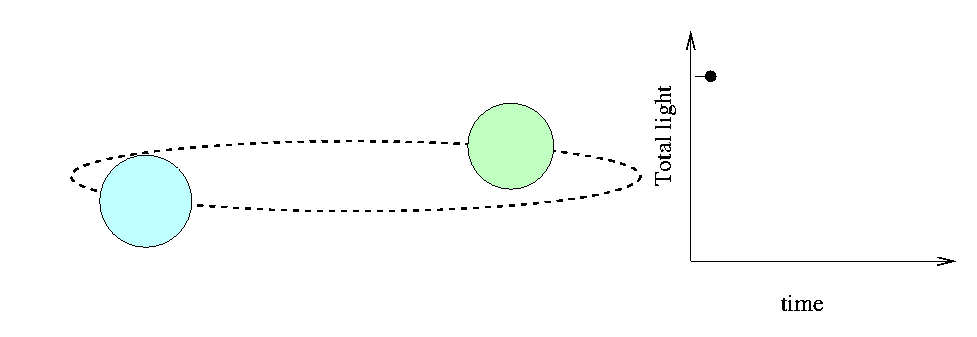
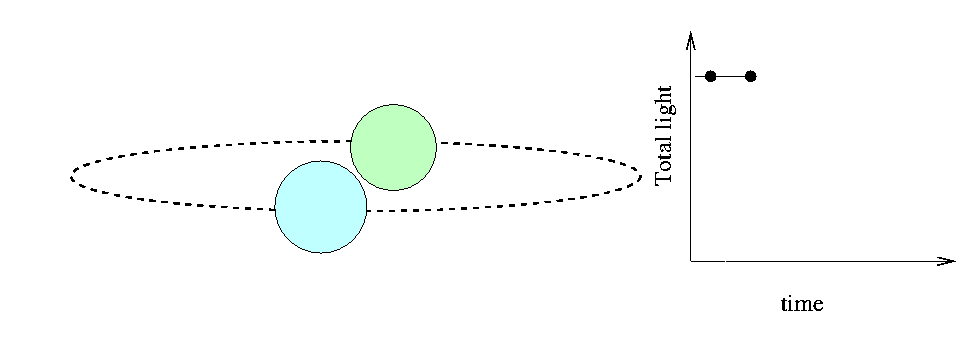
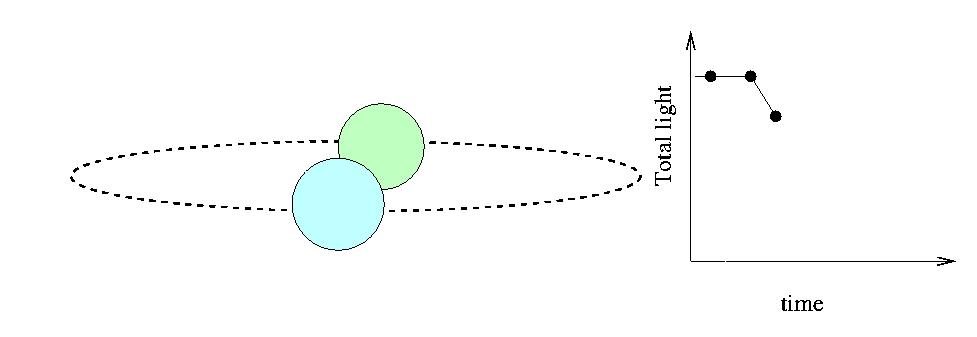
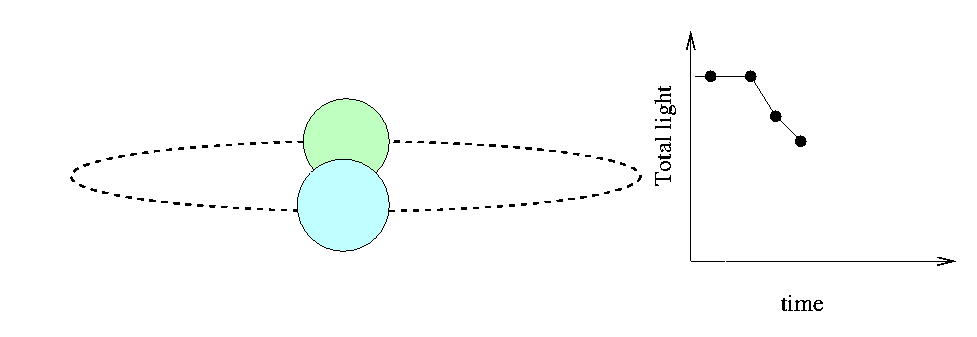

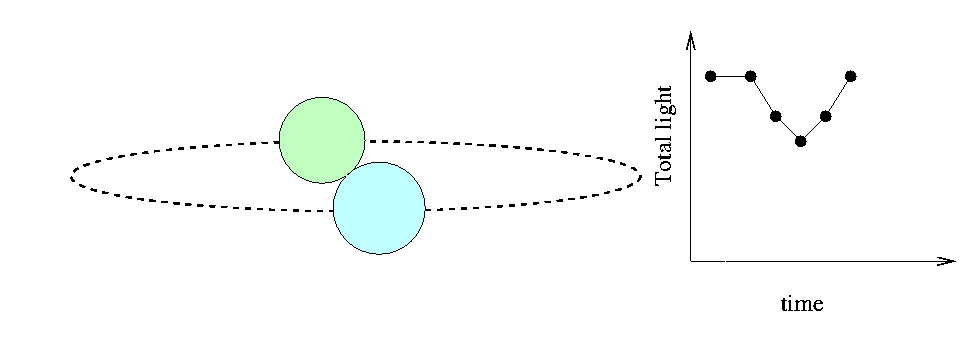
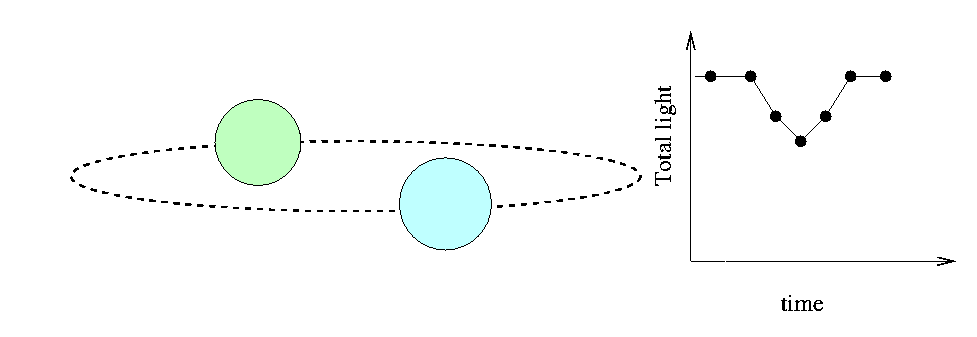
The time interval T between first contact and mid-eclipse depends on the sizes of the two stars and their relative velocity, (VA - VB). There are some complications, of course,
Wait a minute -- we need to know the orbital speeds of the two stars, VA and VB. How can we determine that?
Yes -- use spectra of the system to measure the Doppler shift of each star's absorption lines. If the orbit is circular, then the maximum radial velocity we measure for each star is exactly the same as the tangential velocities VA and VB with which they pass in front of each other.
The star CV Velorum, or CV Vel for short, is an eclipsing binary which shows features from both stars in its spectra. The period of its light curve is P = 6.889 days. Here's a sample of its light curve, from the paper Four-colour photometry of eclipsing binaries. VIII - CV Velorum, light curves, photometric elements and absolute dimensions
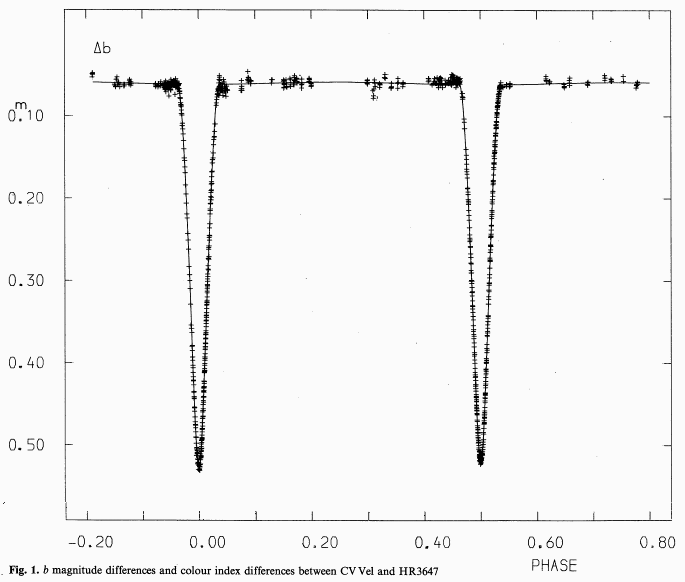
Q: What is the duration of the primary
eclipse in fractions of a period?
The period is P = 6.889 days.
How long is each eclipse in seconds?
Here are a few small segments of its spectrum, taken at a time ("quadrature") when the components were moving nearly directly towards us and away from us, from the paper Spectroscopic observations of eclipsing binaries. III - Definitive orbits and effects of line blending in CV Velorum In this system, the two stars have nearly the same mass, so they orbit their center of mass with nearly the same velocity. The features you see in the spectrum below are shifted by equal amounts away from the rest wavelength of each line, which is halfway between the features.

Q: What is the size of each star's
shift in wavelength?
Q: The rest wavelength of the top set
of lines is 448.1 nm. What is the
orbital speed of each star?
Now, if each star is moving at a particular speed, but in opposite directions, then as they pass each other, their relative speed will the sum of the two speeds. If you know this relative speed, and the time it takes one to pass in front of the other, you can figure out the size of each star.
Q: Assume that the two stars are the
same size. What is the diameter of
each one?
A bit earlier in this lecture, I stated that the diffraction of light waves means that one would have to build an impossibly high telescope to be able to resolve a star like the Sun at a distance of 10 parsecs. It would take a mirror hundreds of meters in diameter!
But, in theory at least, it is possible to combine the light from several small telescopes separated by a similar distance to achieve the same resolution. This technique is called interferometry. Radio astronomers do it all the time.

The shorter the waves, the harder it is to combine them properly. In simple terms, you need to know the distance between the two telescopes to a precision smaller than the wavelength of the light you are combining. To combine optical light waves properly, you need to know the distance between the mirrors to a precision of better than 100 nm. That's hard!
But not impossible. There are several groups who are currently using optical arrays to do interferometry. One of them, Navy Prototype Optical Interferometer (NPOI) , is located near Flagstaff, Arizona.

Small telescopes in each of the huts

send light through big pipes into the Optics Lab, where their signals are combined.

The NPOI can resolve details which are much, much smaller than 1 arcsecond.

Q: What is the resolution of these images
from the NPOI?
In the near future, we can expect to see many measurements of stellar diameters from these groups.
If all else fails, we can make a very rough estimate of the size of a star by assuming that it radiates energy like a perfect blackbody. A "perfect blackbody" is an object which absorbs all the radiation which strikes it, and then re-emits it in a very particular manner.
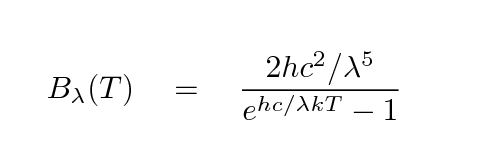

Are stars really perfect blackbodies? Compare a real stellar spectrum to the blackbody model:
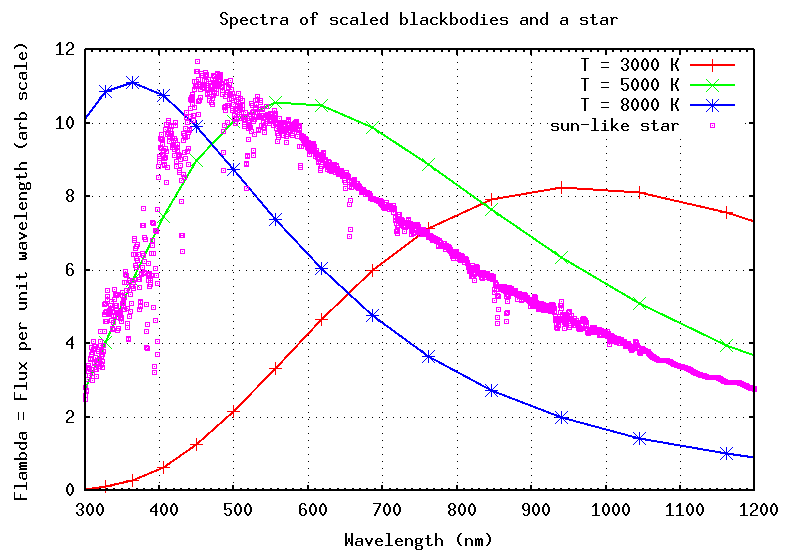
No, real stars aren't perfect blackbodies ... but in some cases, they aren't too far from the ideal model. If we continue with the blackbody approximation, then we can calculate the luminosity of the star -- the power it radiates -- as a combination of its temperature and surface area. For spherical stars, the surface area is A = 4 π R2, so the luminosity L is
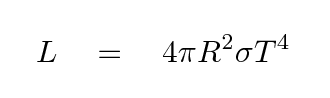
Turning this around, if we knew the luminosity and the temperature, we could figure out the radius.
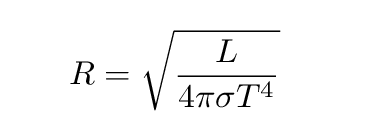
The value of the Stefan-Boltzmann constant σ is roughly 5.67 x 10-8 Watts per square meter per Kelvin4.
Q: How can we estimate the temperature of a star?
How can we estimate the luminosity of a star?
So, just how many stars have well-measured diameters? One estimate comes from the Catalogue of Apparent Diameters and Absolute Radii of Stars (CADARS) - Third edition -Comments and statistics. You can query this catalogue using the Vizier facility. The catalog contains diameters for over 9700 stars. Is it a fair sample of stellar sizes? Take a look at the distribution of measured sizes, in terms of the solar diameter:

(I've cut off the plot at 10 solar radii for convenience --
there are a few much larger stars!)
What fraction of these stars are smaller than the Sun? What fraction of all stars in the galaxy are smaller than the Sun? There is clearly a bias towards large stars -- why?
This is an example of selection bias, which appears again and again in astronomy. Scientists who study the demographics of stars in the Milky Way must be very careful to account for this sort of bias ....
The star Vega has a temperature of about 10,000 Kelvin. Assume that it emits light like a perfect blackbody.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.