Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The European Space Agency built the Rosetta spacecraft (with a little help from JPL ) and sent it on a long journey. Its primary goal is to reach comet 67P/Churyumov-Gerasimenko and place a lander on the surface.
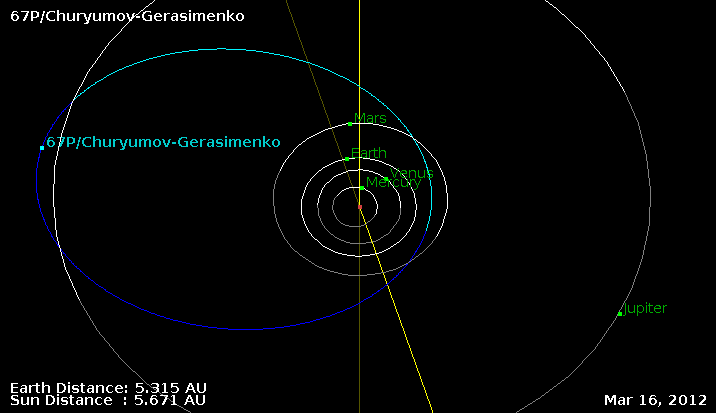
The comet has an orbit in which it spends most of its time far from the Sun, between the orbits of Mars and Jupiter.
Rosetta was launched in March, 2004. The plan was for the spacecraft to reach the comet in 2014.
But one year after it was launched, in March, 2005, Rosetta was right back where it started --- zipping past the Earth just a few thousand kilometers above the the Pacific Ocean off Chile.
Photo: ESA
Photo: ESA
So what was the spacecraft doing near the Earth?
The problem is that it takes a powerful rocket to reach the outer solar system directly -- and such powerful rockets are expensive. Let's do a quick and dirty calculation of the energies involved.
Gravitational Potential Energy (GPE) of a spacecraft of
mass m which is a distance r from a
planet of mass M
G M m
GPE = - -------
r
Increase in GPE if the spacecraft moves from r1 to
a larger distance r2
( 1 1 )
incr in GPE = G M m * ( --- - --- )
( r1 r2 )
Consider these three situations, and figure out how much energy you must give a spacecraft to change its position in each case:
The Rosetta spacecraft has a mass of about m = 6500 kg
The gravitational constant is roughly G = 6.67E-11 N*m^2/kg^2
The mass of the Earth is Me = 5.98E24 kg
The mass of the Sun is Ms = 1.99E30 kg
1. Rosetta is launched from the ground to an altitude
of 1 Earth radius (Re = 6.37E6 km).
2. Rosetta increases its distance from the Earth's surface
from 1 Earth radius to 60 Earth radii (the Moon's distance
from the Earth).
3. Rosetta moves outwards away from the Sun, from roughly
1 AU (the Earth's distance from the Sun, 1 AU = 1.5E11 m)
to a distance of 3.5 AU, where it will meet the comet.
You can see that the amount of energy needed to reach the outer portions of the Solar System is enormous, much larger than that needed just to reach Low Earth Orbit, or even to reach the Moon.
If one has patience, however, one can use a much less expensive rocket and a series of gravity assists to reach the desired location; it just takes time.
This Flash animation shows the trajectory of the spacecraft and its gravity assists from the Earth:
Count the flyby events:
Each of the encounters with Earth increases the spacecraft's orbital energy and size; the encounter with Mars, on the other hand, decreases the orbital energy just enough to cause the subsequent approaches to Earth.
The final leg of the journey, from the final Earth flyby to the meeting with Comet 67P, takes about five years. Scientists will have to wait until the year 2014 to reach the comet.
Q: How old will you be in 2014?
What will you be doing then?
How can it help a spacecraft to fly past a planet? Sure, it will gain speed as it is pulled towards the planet by gravity ... but doesn't it lose that extra speed as it moves away from the planet?
There is a key factor involved. Let's look at a simpler situation to see it clearly. Consider Fred. He has a little rubber ball.
What will happen if he throws the ball at a car parked in the street?
Q: Did the ball pick up extra speed by
bouncing off the car?
Fred repeats the experiment, but this time, he stands out in the street and tosses his ball at a car which is speeding at 50 miles per hour.
Q: Did the ball pick up extra speed by
bouncing off the car?
Why? What's different in this situation?
Which way did the ball get a boost?
What happens to the car as a result?
In some collisions -- including the gravitational encounters between spacecraft and planets -- both momentum and kinetic energy are conserved. If you know the original velocities (magnitude AND direction) of two colliding objects, and their masses, then you can figure out their final velocities.
Fred now goes to a nearby racetrack and tosses his ball in front of a car which is going around in circles.
Even a gentle toss in front of a speeding car results in the ball shooting away from the car at high speed, in the same direction of travel.
Now, replace the racetrack with the Solar System; and replace the speeding car with a planet. You end up with a gravity assist which can greatly increase (or decrease) the speed of a spacecraft.
Figuring out the effect of a planetary encounter on a spacecraft is easiest if you transform into the center-of-mass frame; since planets are so much more massive than spacecraft, this means going into a frame in which the planet is at rest at the origin.
Last modified by MWR 3/8/2005
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.