 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The discoveries of Kepler and Newton make it easy to determine the mass of a star: all we need to do is to find something orbiting around it, measure the period and semi-major axis of the orbit, and plug into Kepler's Third Law. That doesn't sound so hard. In practice, though, it may take a bit more work than you might imagine.
There are two main classes of systems to which we can apply Kepler's Third Law:
When we point our telescopes at a binary star system, we don't always see two individual points of light. The problem is that we can only resolve the members of the binary if
In the second case, two stars orbiting each other at a very large orbital distance, the orbital period turns out to be inconveniently large. Not many astronomers are willing to wait 600 years for one complete revolution. We are left with only a relatively few binary star systems which are close enough to the Sun that we can measure the positions of each star accurately, and which have a short enough orbital period that we can determine it during a single human lifetime.
One of these systems is the bright star Procyon:

If we look at Procyon with a telescope, we see a very bright star of magnitude 0.4; and, if we look very carefully, we can make out a much fainter star nearby, roughly magnitude 11:
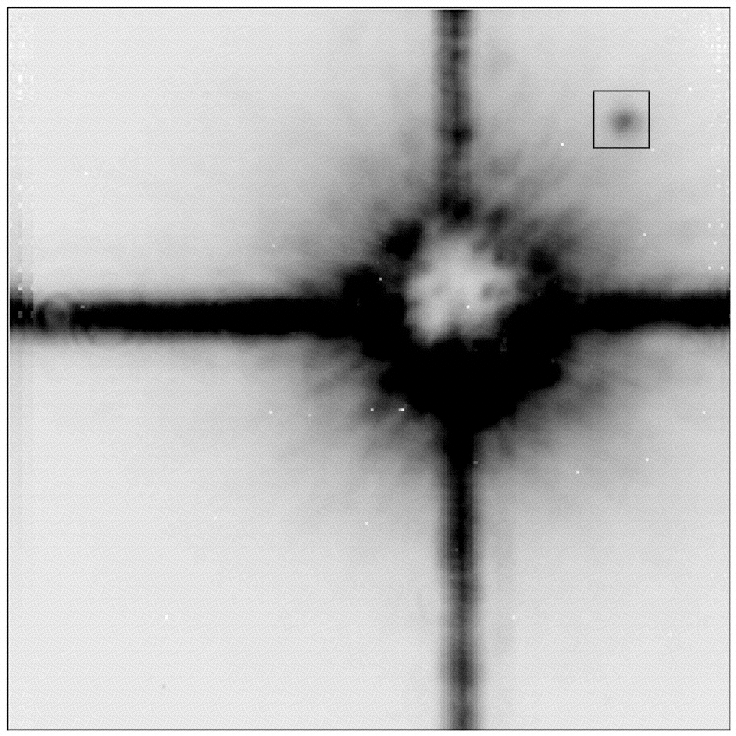
CoCo coronagraph image of Procyon A-B taken 1995.09
with the NASA IRTF 3 m telescope.
This is a 10 s exposure taken in K band with the primary
positioned behind the apodized, occulting mask.
This very faint companion (Procyon B) was first observed by Schaeberle at Lick Observatory in 1896. Since then, astronomers have followed its motion around the bright star (Procyon A).
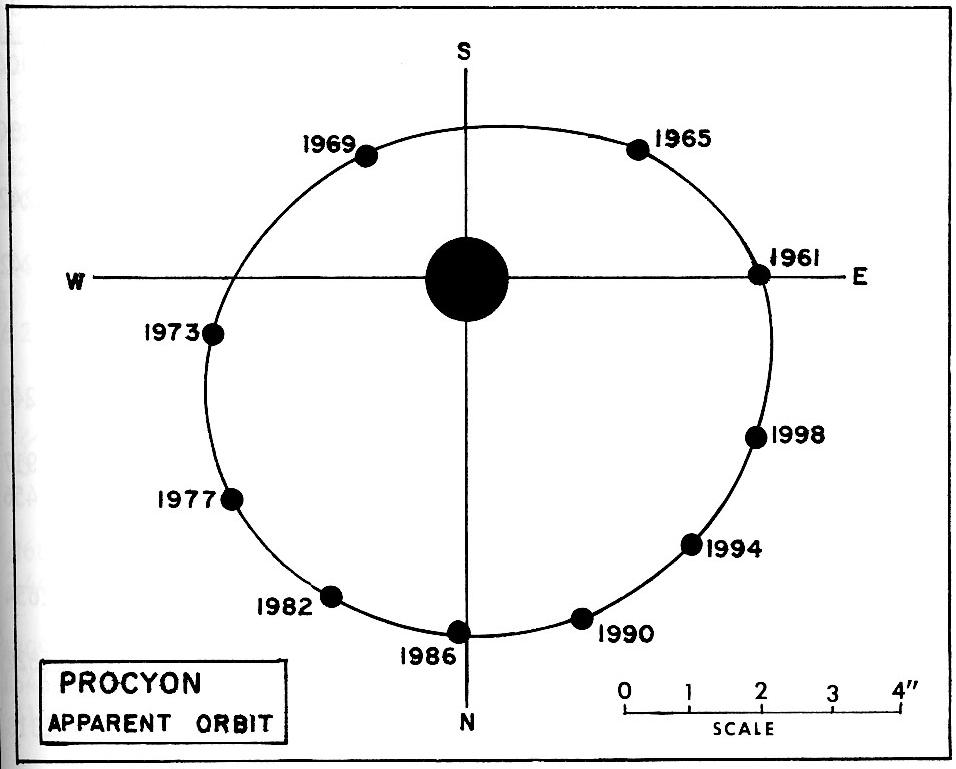
This figure taken from Burnham's Celestial Handbook, vol 1
Now, for the moment, let's assume that we are observing this orbit face-on. This will make the calculations simpler...
Q: What is the period of Procyon's orbit?
Q: What is the apparent angular size of the
semi-major axis?
In order to use Kepler's Third Law to determine the mass of the system, we need to have the period -- check -- and the linear size of the orbit. Whoops. All we have so far is the angular size of the orbit. To convert angular size (degrees or arcseconds) to linear size (meters or AU), we need the distance to the star and a little trigonometry.
Fortunately, we do know the distance to this star. Hipparcos finds the parallax of Procyon to be π = 286 +/- 1 mas.
Q: What is the distance to Procyon?
Q: What is the linear size of the semi-major axis?
Express your answer in Astronomical Units (AU).
Right. Now we have both the period, in years, and the semi-major axis, in AU. We can use Kepler's Third Law to measure the total mass of the two stars together.
2
Period (in years) 1
----------------------- = ----------------------------
3 mass of system (solar masses)
semi-major axis (in AU)
Q: What is the total mass of both stars in the
Procyon system, in terms of solar masses?
We assumed in our calculations above that we are observing the orbit of Procyon "face-on"; that is, as if we were floating high above the plane of the orbit.

But in real life, we are usually not so lucky. In most cases, we observe a binary star orbit at some inclination angle i away from face-on.
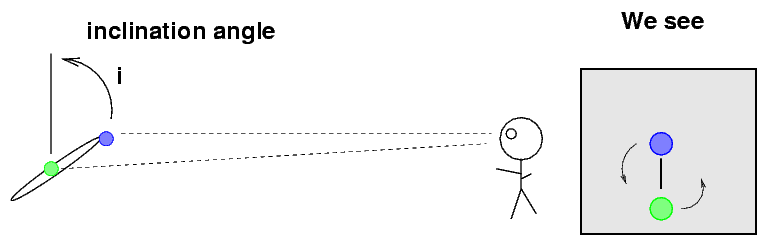
That means that the size of the orbit we observe is actually smaller than the true size of the orbit.
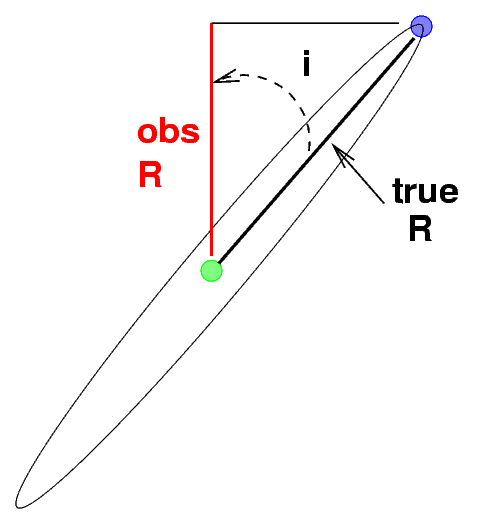
Q: What is the relationship between the observed
semi-major axis and the true semi-major axis?
In the case of Procyon, the inclination of the orbit is estimated to be about i = 31 degrees.
Q: Correct your value for the observed semi-major
axis for this inclination. What is the
new semi-major axis?
Q: Use the corrected semi-major axis to compute
the mass of the stars in the Procyon system.
How does it compare to your previous mass estimate?
This gives you a flavor for the factors involved in correcting measurements of binary stars for the inclination. However, the proper corrections require quite a bit more work. It isn't necessary for this course, but if want to know more, read some lectures from the Astrophysics course SPSP 440 on the topic:
Most binary stars are so far away that the light from their components merges into a single blob of light in our telescopes. We can't measure the position of each star individually. Rats.
But that doesn't mean that we are stuck. We can STILL figure out the masses of some of these binary systems by using spectroscopy: breaking the light up by wavelength. In some cases, we can figure out the motions of each star by identifying its absorption lines in the combined spectrum.
The simplest type of spectroscopic binary to analyze is one which is exactly edge-on to our view: at an inclination angle of i = 90 degrees.

As the two stars orbit around each other, we will see periodic eclipses. In the CV Vel system, for example, the light curve (magnitude versus time) looks like this:
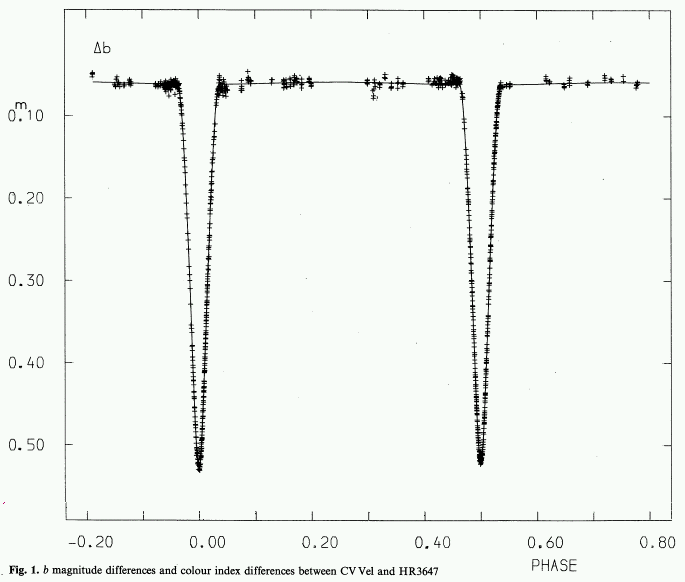
The period of the orbit is easy to measure: it is simply the time between one eclipse and the SECOND following eclipse.
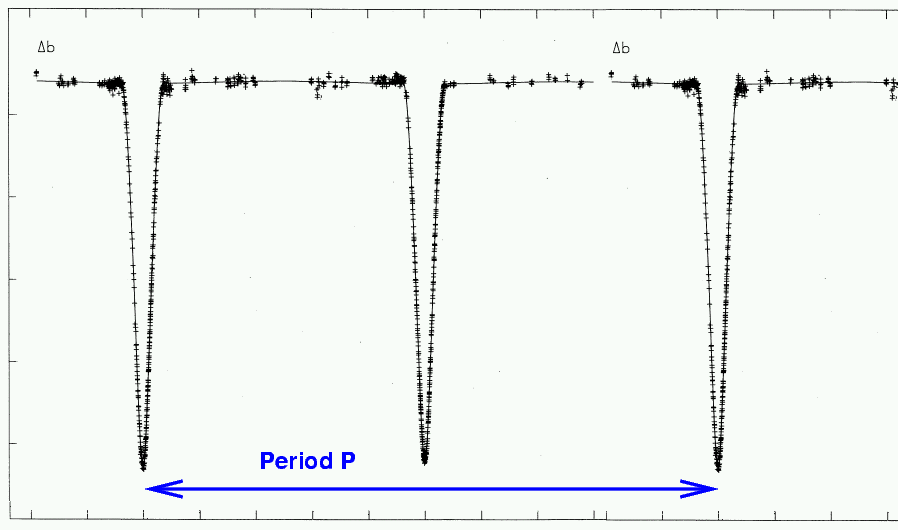
Q: Why do we skip over the FIRST following
eclipse in order to measure the period?
In the case of CV Vel, this period is P = 6.889 days .
In order to use Kepler's Third Law, we need period and semi-major axis. How can we find the size of the orbit if we can't even see the orbit? We use a little clever calculation.
The spectrum of this binary star shows two sets of absorption lines, one from each star. The line produced by singly-ionized magnesium atoms, for example, has a rest wavelength of 448.1 nm. In the spectrum of CV Vel, we see two lines. Their positions shift as the two stars move around each other, but the maximum separation looks like this:
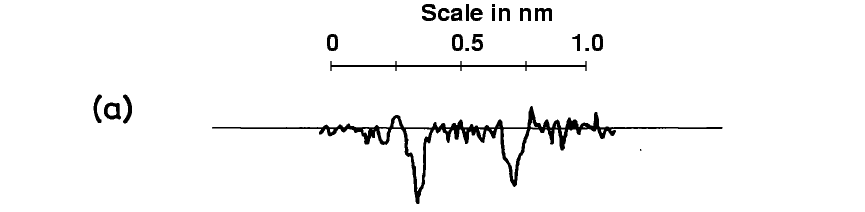
We can figure out the speed of each star from the Doppler shift in its lines.
Q: What is the shift in wavelength (away from the center)
of the line created by each star?
Q: What is the orbital speed of each star?
Now, if you know the speed of each star, and if you assume that it maintains this speed as it moves around a circular orbit
Yes, yes, we are making a number of approximations. In real life, astronomers deal with the complications caused by elliptical orbits and changing speeds, but we will ignore those for now...
then we can figure out how large the orbit must be:
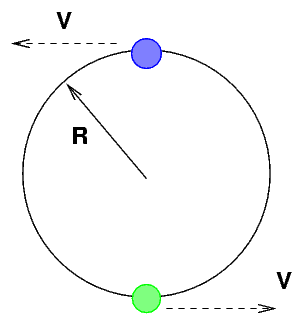
Okay, it's time for you to put it all together.
Q: Assume that both stars in CV Vel move in
perfect circles. What is the orbital
radius R for each star? Express your
value in AU.
Q: What is the separation between the two stars?
This serves as the semi-major axis "a" in Kepler's
Third Law when the two objects are comparable
in mass to each other.
Q: What is the total mass of the CV Vel system?

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.