Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In order to understand how astronomers measure stellar masses, we need to take a step back and look at one particular chapter in the history of astronomy. In the late 1500's, a Danish nobleman named Tycho Brahe built the world's premier observatory on an island off the coast of Denmark.
Even though the telescope had not yet been invented, so that all measurements had to be made with the naked eye, Tycho's instruments and careful procedures allowed him and his assistants to determine the positions of stars and planets to an accuracy of less than 1 arcminute.
Tycho accumulated a great body of measurements over several decades. After his death in 1601, this collection of data passed to his assistant, a brilliant mathematician named Johannes Kepler.
Kepler studied the tables of planetary positions, especially those of Mars. In the year 1609, he published a book, Commentaries on the Motions of Mars, in which he stated two startling new properties of planetary motion: they are now known as Kepler's First Law and Kepler's Second Law:
Kepler continued to pore over the tables as the years went by, seeking some simple underlying connection between the various properties of planetary orbits. In 1619, he finally found it:
" ...if you want the exact moment in time, it [the correct form of the law] was conceived mentally on 8th March in this year one thousand six hundred and eighteen, but submitted to calculation in an unlucky way, and therefore rejected as false, and finally returning on the 15th of May and adopting a new line of attack, stormed the darkness of my mind. So strong was the support from the combination of my labour of seventeen years on the observations of Brahe and the present study, which conspired together, that at first I believed I was dreaming, and assuming my conclusion among my basic premises. But it is absolutely certain and exact that the proportion between the periodic times of any two planets is precisely the sesquialterate proportion of their mean distances..." [Harmony of the World, Linz, 1619]
Kepler's Third Law states that the period of a planet is related to its distance away from the Sun in a particular way; he used the word sesquialterate to describe it, which is a fancy way of saying this:
Does this really work? Let's find out. Consider the following orbits.
2 3
Orbiting body Period P P Semi-major axis a a
(years) (AU)
---------------------------------------------------------------
Mercury 0.241 0.387
Earth 1.000 1.000
Jupiter 11.86 5.20
Pluto 247.9 39.53
Moon 0.0748 0.00257
Callisto 0.0457 0.0126
----------------------------------------------------------------
First, we need to fill in the columns in the table above with values for period squared and semi-major axis cubed. Next, we take Kepler's Third Law and re-arrange it a bit.
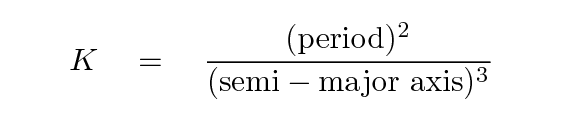
Using the values in the table above, calculate the value of this constant in Kepler's equation for each of the orbits:
2 3
Orbiting body P a const
(years) (AU)
---------------------------------------------------------------
Mercury
Earth
Jupiter
Pluto
Moon
Callisto
----------------------------------------------------------------
Q: Was Kepler right? Do all orbits follow this
simple relationship?
Hmmmmm. Kepler's relationship seems to hold for the major planets we checked -- Mercury, Earth, Jupiter, Pluto -- but it doesn't work for the Moon or Jupiter's moon Callisto. Why? Is there some explanation?
Kepler's Third Law certainly does hold for each of the planets as it revolves around the Sun. Why doesn't the same constant appear when we compare the square of the period of the Moon's orbit around the Earth to the cube of its orbital radius?
The answer: because the Moon isn't circling around the Sun -- it is orbiting around the Earth.
Let's look more closely at the values for the constant in the examples shown above.
Orbiting body central body const mass of central body
---------------------------------------------------------------------
Mercury Sun 1.002 2 x 10^(30) kg
Earth Sun 1.000 2 x 10^(30) kg
Jupiter Sun 1.000 2 x 10^(30) kg
Pluto Sun 0.995 2 x 10^(30) kg
Moon Earth 330,000 6 x 10^(24) kg
Callisto Jupiter 1000 2 x 10^(27) kg
---------------------------------------------------------------------
Q: Do you see a pattern here?
Yes! The larger the mass of the central body, the SMALLER the value of the constant connecting orbital period to orbital radius. In fact, it looks as if we express the input values in convenient units, we get a very convenient output value.
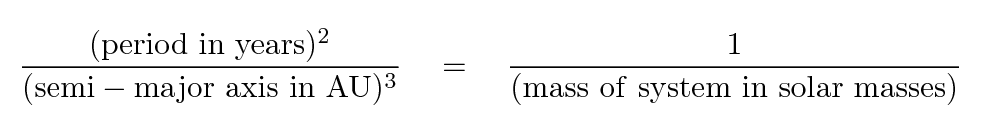
Kepler slogged through years, and I mean YEARS, of tedious calculations to turn Tycho's tables of planetary positions into a single set of homogeneous data, and then sifted through the data to find simple connections between different quantities. His laws were empirical: he could describe WHAT the connections were, and how to calculate them, but he did not (correctly) explain WHY these particular relationships should exist.
Kepler did speculate on the reasons for the "Harmonic Law," as he called it, but his ideas were wrong. That doesn't diminish the importance of his work in any way, in my opinion.
Some forty years later, a young English student, Isaac Newton,
found his own set of fundamental rules governing the motions of bodies.
To these rules, Newton added one more which was especially useful in the celestial realm, where the dominant force between objects is gravity.
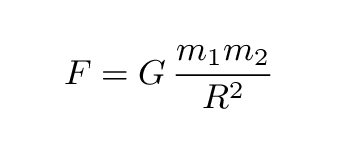
Using these rules as starting points, Newton was able to derive all of Kepler's Laws. He was able to show that the orbits of objects under the force of gravity must be ellipses (that's a hard one), that the velocity of a planet will increase as it approaches the Sun (that's an easy one), and that the relationship between orbital period and orbital radius must be exactly as Kepler had discovered.
We can follow Newton's reasoning for the simple case of a circular orbit; it won't take too long. Just fill in the blanks.
Step 1: If an object is moving in a circular path of radius R with velocity v, some force must be pushing or pulling it towards the center of the circle. How large must that centripetal force be?
Step 2: In the case of a planet (mass m) moving around the Sun (mass M), gravity provides this force. How strong is the force of gravity in this case?
Step 3: Setting these two forces equal to each other gives us a relationship between the square of the velocity v and the radius R.
Step 4: If a planet moves around a circle of radius R with speed v, can you express the velocity in terms of the period P?
Step 5: Take this expression for velocity and square it.
Step 6: Almost there! Just re-arrange things so that all the terms with P go on the left, and all the terms with R to on the right. What do you get?
Well, fine: what does all this have to do with measuring the masses of stars?
So, if we can determine both the orbital period and the orbital radius of something orbiting around a star, then we can infer the mass of that star.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.