
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
If you look in any astronomy textbook, you'll find somewhere a diagram of the Milky Way Galaxy with dimensions: the disk of our galaxy is about the disk is about 20,000 parsecs = 20 kilo-parsecs = 20 kpc across, and the Sun is about 8,000 parcsec = 8 kpc from the center. How do we know these dimensions?
Is it possible to use parallax to measure the distance to the center of the Milky Way? The best parallax measurements from the Hipparcos satellite are around 0.003 arcseconds, or 8 x 10^(-7) degrees. Let's see ....

Q: How large would the parallax angle be?
Hmmmm. Parallax won't do the job. Fortunately, there are two approaches which we can try to determine distances throughout our Galaxy (and even to other nearby galaxies).
Suppose that see a cluster of stars somewhere in our Galaxy:

If we take pictures of the cluster through both B and V filters, then we can measure the B and V magnitudes of each star. We can then make a color-magnitude diagram of the cluster, like this:

Pay special attention to the location of the main-sequence turnoff point in this diagram:
We can compare the location of the turnoff point to HR diagrams based on models of stellar evolution. Lionel Siess of the Institut d'Astronomie et d'Astrophysique is one of many astronomers who makes detailed computer models of stars and watches them evolve with time. The figure below shows the (B-V) color and absolute V magnitude of stars of different ages.

Can you pick out the location of the main sequence turnoff point in these theoretical HR diagrams? By comparing the turnoff point in the observed and theoretical diagrams, you can estimate two important properties of the cluster.
Yes, yes, we are ignoring possible differences in metallicity between the cluster and the models. We are also ignoring possible reddening and extinction of the observations due to dust...
Q: What is the age of stars in the cluster NGC 104?
Q: What is the distance modulus (m - M) for stars in
the cluster NGC 104?
Q: What is the distance to the cluster NGC 104?
(Hint: scroll down just a bit)
Hint:

In some circumstances, astronomers can use individual stars as standard candles to measure distances across the galaxy. A "standard candle" is simply an object of known luminosity. If we know the total power emitted by a star, or, equivalently, we know its absolute magnitude, then it may be used as a standard candle. Finding distances with standard candles is easy:
So, all we need is some type of star we can use as a standard candle. Fortunately, Nature has provided two types of stars which are easy to recognize, and easy to use.
If you take a single picture of a distant cluster of stars, you see ... a bunch of stars.

You can measure the brightness of each star in the cluster. Then you have a bunch of numbers ....
But if you take a second picture of the cluster, and then a third, and then another, and another, and another, and measure the brightness of all the stars in all the pictures, THEN you discover something interesting:

Image courtesy of
J. Hartman
and
K. Stanek
( Harvard CFA )
Most of the stars remain the same brightness all the time, but a small fraction vary, growing brighter and fainter, brighter and fainter.

Many of these variable stars have a set of common features:
We call this class of variable star RR Lyraes, after one particular member, the star RR in the constellation of Lyra.
Oh, and one more thing they have in common: they all produce roughly the same power. Look at the magnitudes of a set of RR Lyrae stars in a cluster called Draco (taken from a paper by Bonanos et al. ):




If they emit the same amount of light, then we can use them as standard candles. All we need to do is find out their absolute luminosity, and then we're set. It turns out that RR Lyrae stars are significantly brighter than the Sun. To a rough approximation, we can say they all have
RR Lyrae stars: (average) absolute mag M = 0.6
Their colors vary as they pulse, but typically lie between (B-V) = +0.20 and (B-V) = +0.50.
Q: Where do RR Lyrae stars fall on the HR diagram?
So, using this absolute magnitude, can you figure out how far away from Earth the star RR Lyrae is?

Hint:

Cepheids are another class of variable stars which may be used as standard candles. They are both better and worse than RR Lyrae stars:
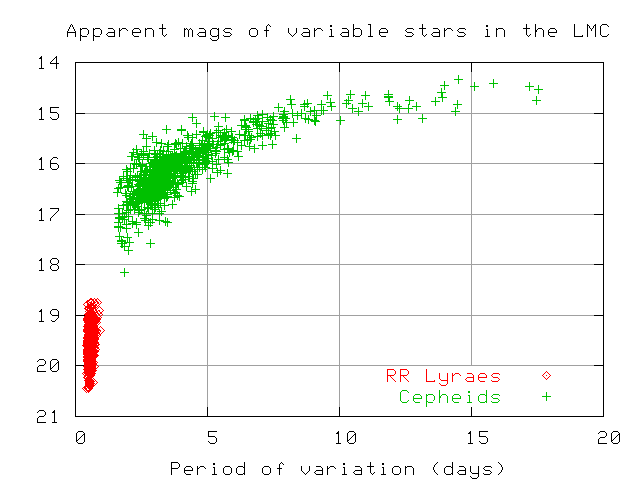
Hey! How can we use Cepheids as standard candles if they don't all have the same luminosity? Well, take a look at this diagram; it shows the apparent magnitude of stars in a distance cluster called the LMC, plotted as a function of their period.
Thanks to the MACHO group
Notice two things:
However, there is a saving grace: the absolute magnitude of a Cepheid variable star is correlated with its period. Longer periods mean more powerful stars. This is especially clear if one plots the magnitude of stars against the logarithm of their periods:
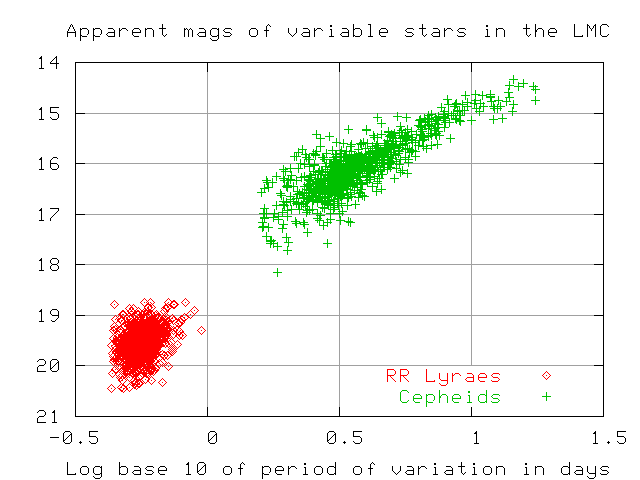
It is possible to make a simple equation which will predict the absolute magnitude of a Cepheid star, given its period. One analysis suggests
Cepheids: (average) absolute V mag M = -1.0 - 2.8 * log(Period)
The colors of Cepheids cover quite a range, due to their wide range of masses and their variations as they pulse; to a rough approximation, they span (B-V) = +0.5 to +1.0.
Q: Where do Cepheid stars of period P = 10 days fall on the HR diagram? Q: Where do Cepheid stars of period P = 100 days fall on the HR diagram?
So, all you have to do is
It's a bit more work than for RR Lyrae stars, but since Cepheids are brighter, you can use them to measure greater distances.
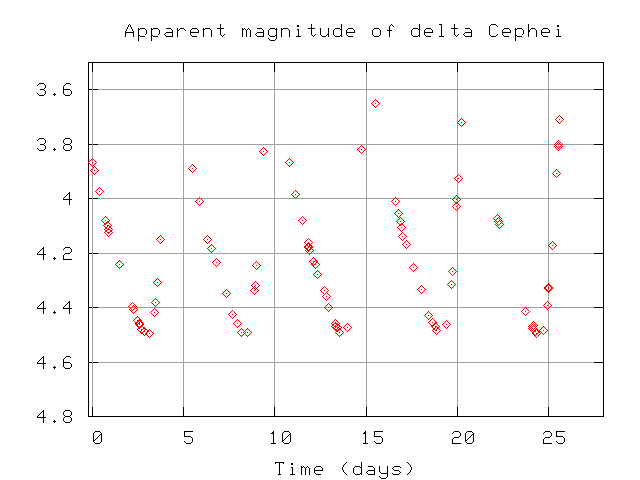
Give it a try: below are some measurements of one Cepheid star (delta Cephei, the prototype of its class). Can you figure out its distance away from the Earth?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.