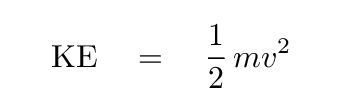
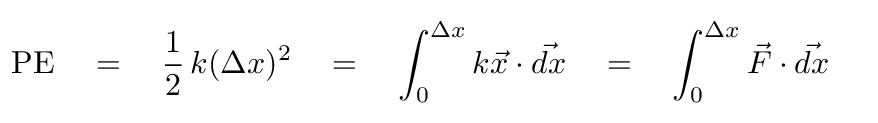
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, we look at the energy associated with a wave -- both the energy within some small section of it, and at the rate at which it transmits energy to its medium.
When a wave reaches a piece of string, it affects that piece in two ways:
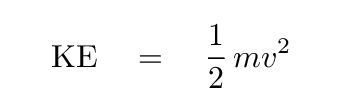
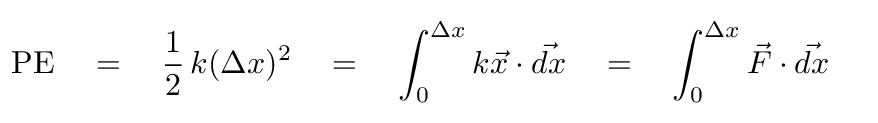
Our discussion will use as an example a wave travelling along a string, but the results may be applied to many other types of waves. Let's assume that our string has properties
Further, we'll assume that the vertical position of the string at any location and at any time can be written as some function
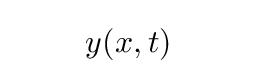
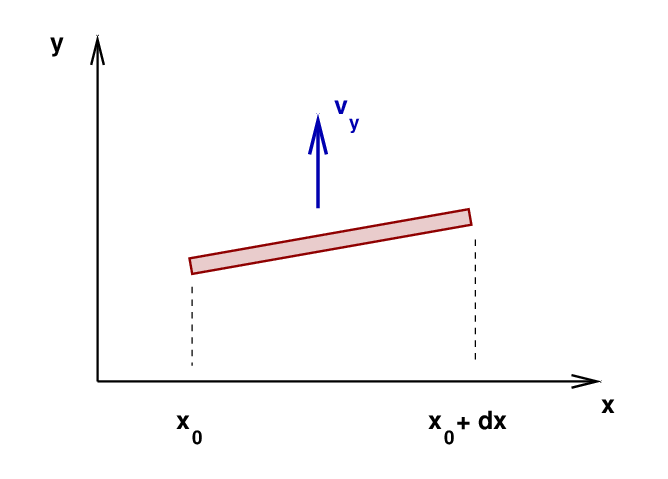
We'll focus on one little tiny piece of the string as it moves vertically upward with speed vy. How much kinetic energy does this little piece have?
The kinetic energy of this tiny section will be tiny itself, so we'll call it dKE -- just as we call a tiny distance in the x direction dx.
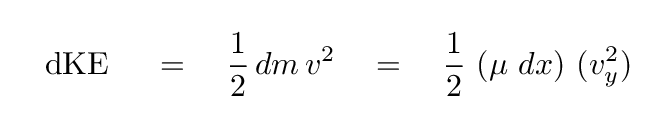
What is the vertical speed of the string? It's simply the partial derivative of y-position with respect to time.
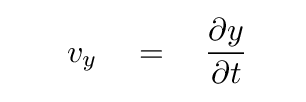
Thus, the kinetic energy of this tiny piece of the string can be written as
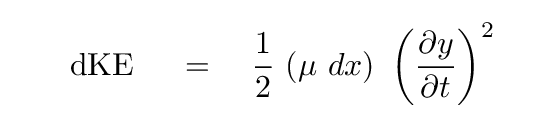
Potential energy? Why should a piece of string have potential energy? The answer is simple: because as the wave passes through the string, it STRETCHES the string. Stretching the string requires a force to act over some (tiny) distance, performing some (tiny) work; that energy equivalent to that work is stored as a sort of spring potential energy inside the stretched string, ready to be released when it relaxes.
But how much energy is stored inside the string?
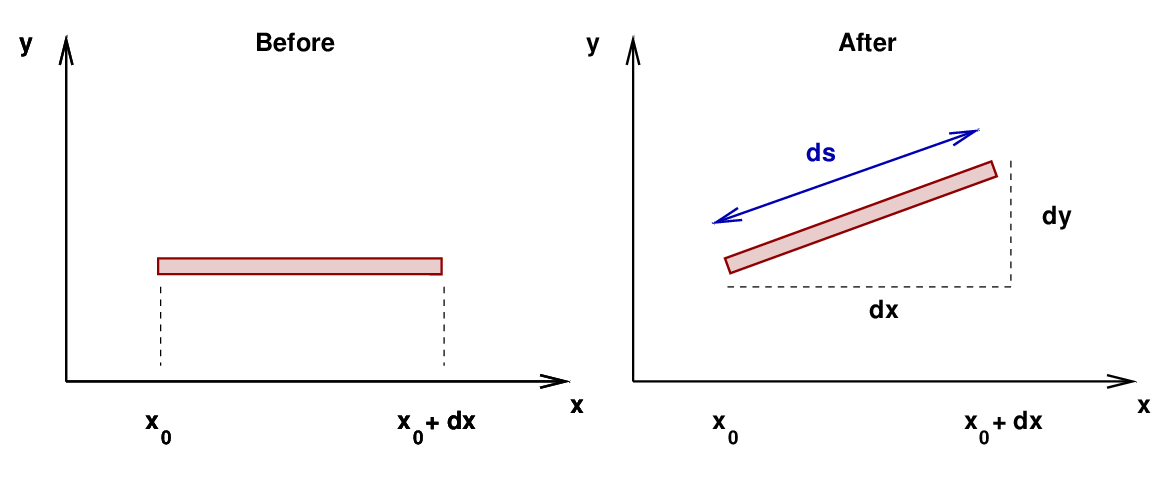
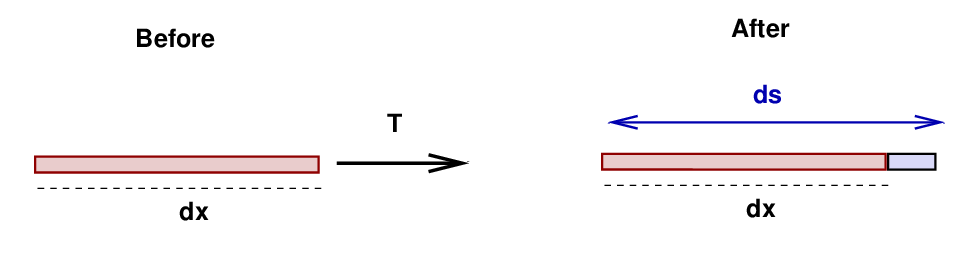
Q: What is the length of the little section BEFORE it is stretched? Q: What is the length of the little section AFTER it is stretched? Q: How much has it increased in length?
The first two answers are obvious:
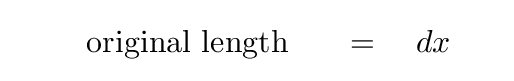
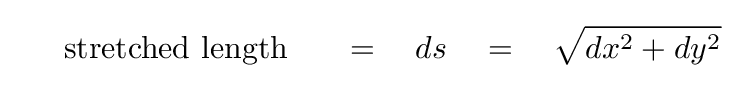
The final question has a simple, but unsatisfying, answer:
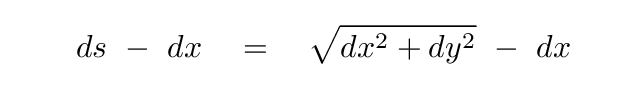
However, if we assume that all vertical displacements are small compared to the length of the string, then it follows that the triangle in the figure above must be a long, skinny one: dx ≫ dy.
Q: Use the fact that dx ≫ dy and the binomial expansion
to simplify the equation for difference in length.
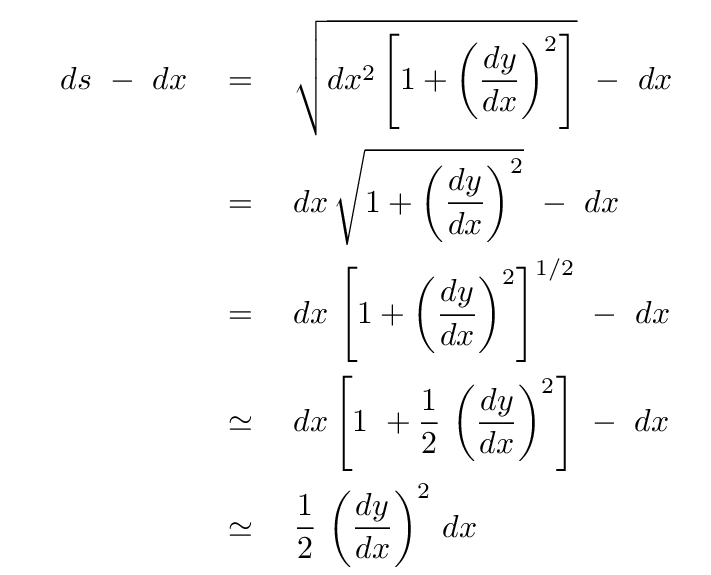
Now, since we are looking at the position of the string at one moment in time, we can convert this to a partial derivative.
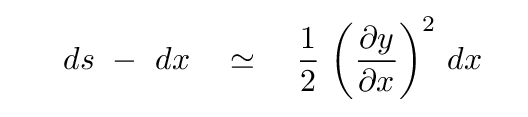
How much energy has been stored in the string via this stretching? We can find the answer by computing the work done on the string by the tension force in order to pull it from an initial size dx to the slightly longer length ds.
In general, the work done by a force is
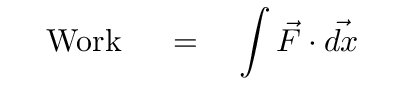
In this case, the displacement over which the force acts is very very small, so we are really computing a tiny amount of work dW.
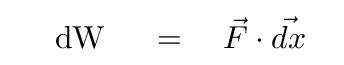
The tension pulling the string is clearly parallel to the extension in length, so the dot product becomes a simple multiplication.
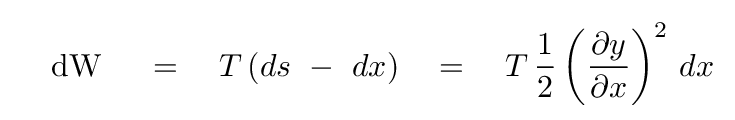
All the work done by that tension force is stored in the string as a sort of spring potential energy, so we can write
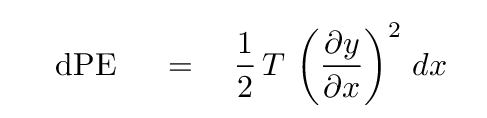
We can now add together the kinetic energy of a little piece of string and its potential energy to find the total energy of this little section.
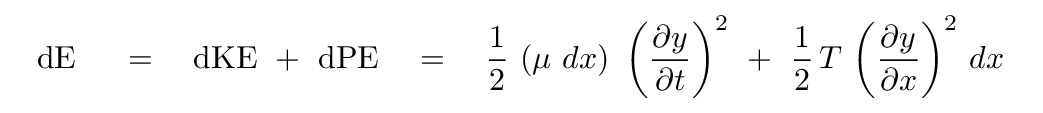
Another way to express this is as a "linear energy density", which would have units of Joules per meter. That would be
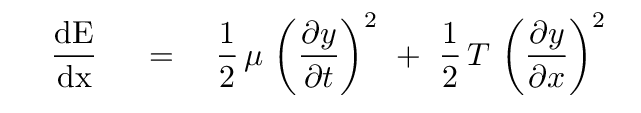
In order to compute the energy of some macroscopic piece of string, one would need to integrate this expression over the length of the string. That job will be easier if we pick some particular functional form for the wave. Let's choose a simple sinusoidal travelling wave:
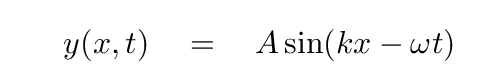
Q: Can you write an expression for the linear energy density
of this wave?
The partial derivatives of the wave equation are
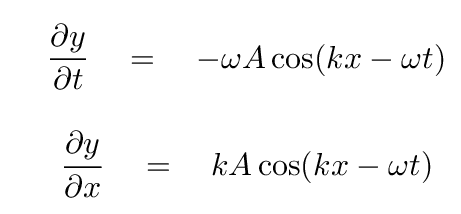
So the linear energy density of the wave is
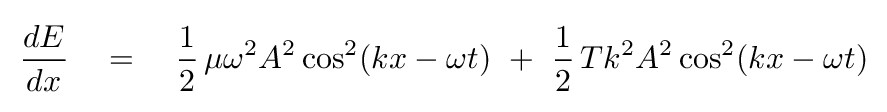
Suppose that we pick some particular section of string -- covering exactly one full wavelength -- and watch as a wave runs through it. Which is larger: the kinetic energy of this section, or the potential energy?
Q: Over a section of string one wavelength long, which is larger?
a) the kinetic energy
b) the potential energy
c) they are the same size
d) can't tell without more information
Which is correct? You'll have to do a homework problem to find out ...
We've answered the question "how much energy does one section of a wave contain?" But there's another, related, question which frequently arises when one studies waves moving through some medium: how much of the wave's energy is transferred to the medium over a period of time? In other words, what is the power of the wave?
You see, before a wave enters some region of a string (for example), the string is motionless and at equilibrium; one can define its energy in this state as "zero." But when the wave reaches some section of string, it causes that section to oscillate up and down, and stretch as well. The wiggling, stretching string has more energy now than it did before.
What is the rate at which energy is transferred to the string?
Consider the string shown below in two snapshots. Let's concentrate on the section highlighted in red. In the first snapshot, at time t0, the string is at rest. In the second snapshot, taken a time Δt later, that section has been set in motion by the wave.
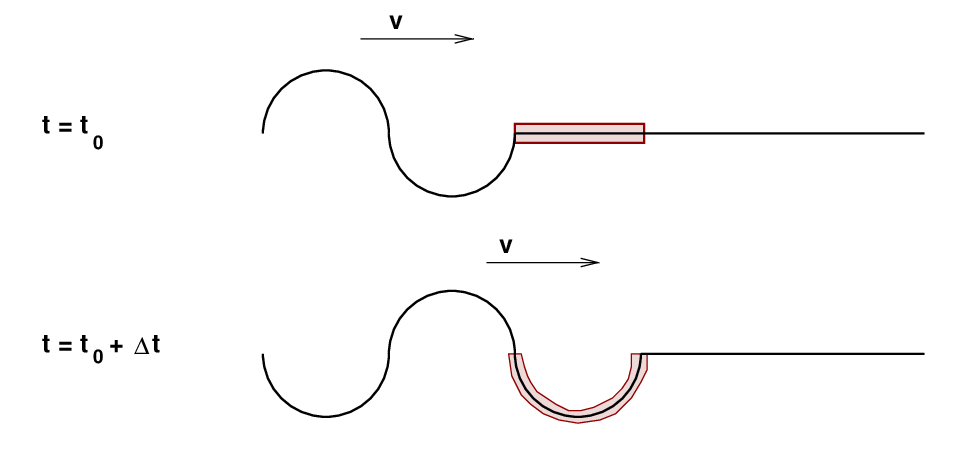
If the wave travels at speed v down the string, then the length of this section is
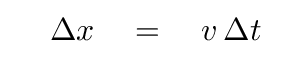
The total energy of this little section of string can be written
No, I haven't derived this. You'll do most of the work yourself when you finish that homework problem mentioned earlier.
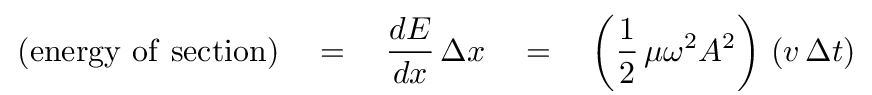
The power transmitted by the wave is simply this amount of energy that it has given to the string, divided by the time it took.
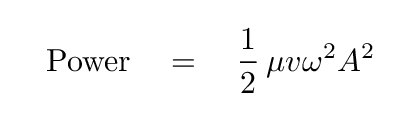
This is just one way to write the power carried by a wave; in the case of a wave travelling down a string, one could also write an expression in which the variables μ and ω are replaced by T and k.
Do the units work out properly? Sure! If we collect the terms like so,
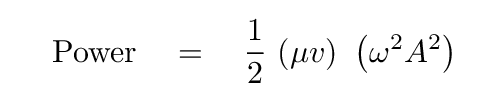
you can see that the first term on the left is (mass encountered, divided by time), while the second term is (velocity squared). The units are therefore good old Energy = (mass) times (velocity squared), divided by time. Thus, power.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.