Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Q: Can you tell the difference between these two sounds?
That was easy: sample A had a lower pitch, or lower frequency, while sample B had a higher pitch.
Q: What about these two sounds?
Believe it or not, those two sounds have exactly the same frequency: 220 cycles per second, or 220 Hz. A musician might refer to it as A3.
Same frequency -- but NOT the same sound. Why not? What could be different?
Let's try another pair:
Q: What is the difference between these two sounds?
Once again, both have a fundamental frequency of 220 Hz -- but they certainly are easy to distinguish.
One of the following sounds is created by a real-life instrument.
Q: Which of these sounds was produced by a real-life instrument?
What instrument was it?
That was a bass flute.
It turns out that real instruments have distinct sounds -- even when they all play the same note. For example, consider the following:
Q: Which two instruments were those?
The first was the bass flute (again), and the second was a horn.
One more test, again -- as always -- using sounds with a fundamental frequency of 220 Hz.
Q: Which two instruments were those?
Sample X was a viola, sample Y a piano.
How is it possible for humans to recognize different instruments? What's causing the difference in the sounds?
The key is that almost all instruments produce more than a single frequency when they play a note. In most cases, an instrument will create a fundamental frequency with a large amplitude, but add to that smaller amounts of harmonics: integer multiples of the fundamental frequency. Different instruments give rise to different combinations of the harmonics, and thus to sounds that seem different to our ears.
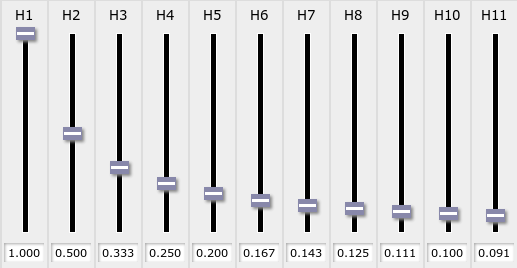
I recommend using this free, on-line tool to play with combinations of harmonics:
Thanks to meettechniek.info
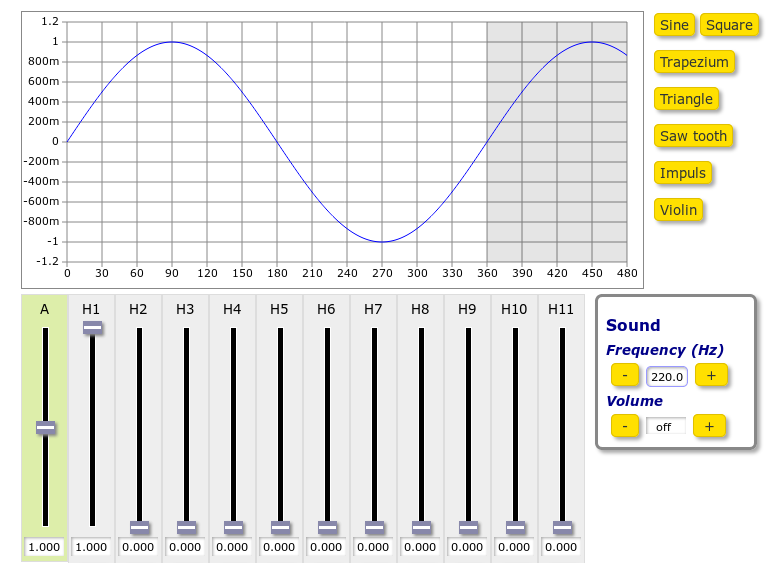
The default, shown above, is a simple sine wave at the fundamental frequency.
Q: What would the Fourier series of this sound be?
One can move the sliders below the graph up or down to add various amplitudes of waves which have twice (H2), thrice (H3), four times (H4), and so forth, times the fundamental frequency. As one moves the sliders,
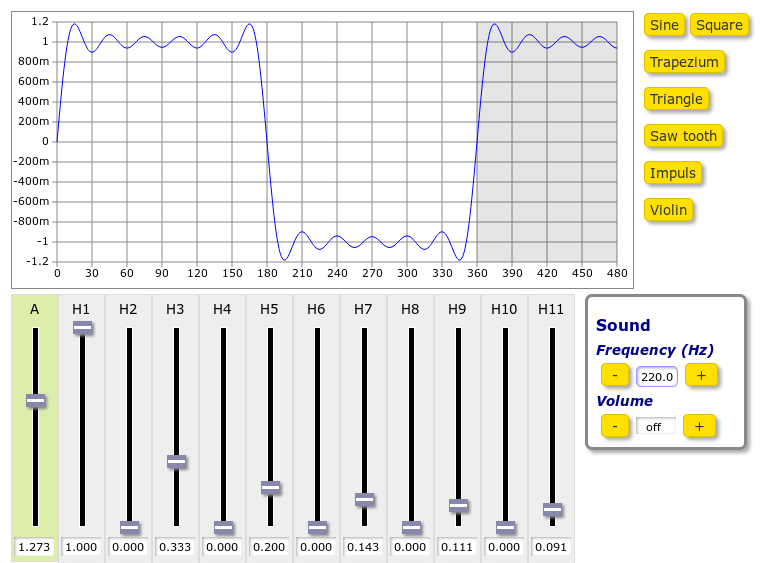
Try the following combination:
Q: How would one write the Fourier series of this sound?
Several common waveforms are built into the application. A "square wave" looks, well, square.
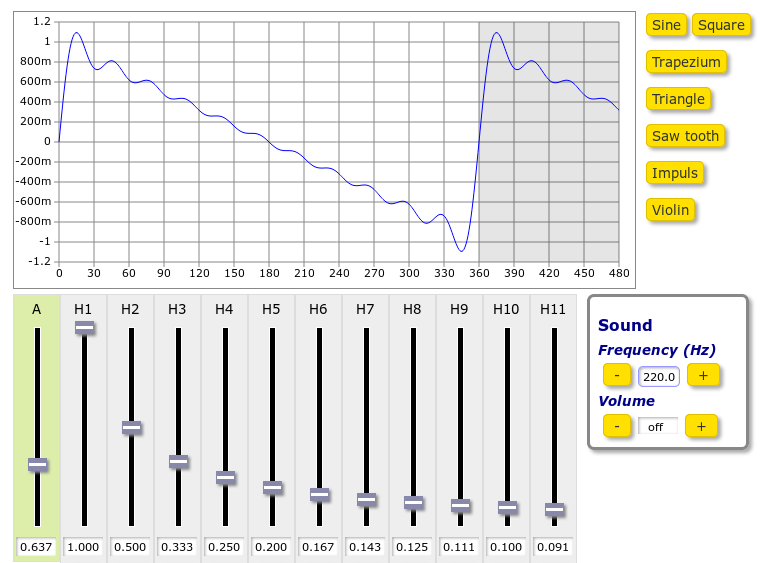
A "sawtooth wave" sounds pretty annoying, in my opinion, but it is composed of all the harmonics, combined with steadily (quadratically?) decreasing amplitudes.
Musicians have a fancy word to describe the character of the sound produced by different instruments: timbre.
This mixture of overtones produced by a particular instrument depends on the physical nature of the instrument: how do its strings vibrate? How do waves of different frequencies interfere within its chamber? What sort of ripples are excited in its surface membrane?
We can't very easily play with sliders to create just the right mixture of harmonics to replicate the sound of a violin, or a horn, or a flute ... but it's not quite so hard to go the other way. Given a sample of the sound of some instrument, we can figure out the mixture of frequencies within it. All we have to do is perform a Fourier analysis.
For example, remember the simple 220-Hz sine wave?
If we compute the coefficients of the Fourier series for a wide range of frequencies, and then plot the size of each coefficient as a function of frequency, we'll end up with a frequency spectrum which looks something like this:
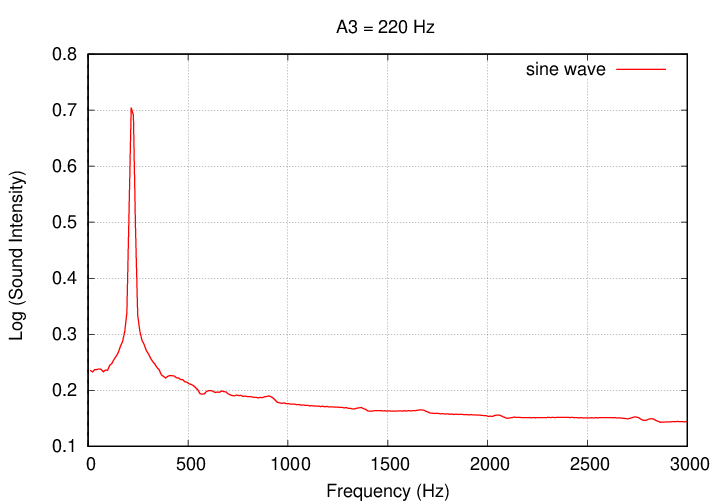
Spectrum created with
Audacity
Pretty simple -- the only frequency with a large amplitude is 220 Hz.
The sawtooth wave, on the other hand, has significant contributions from many harmonics.
Spectrum created with
Audacity
Does that sequence of peaks in the frequency spectrum remind you of something?
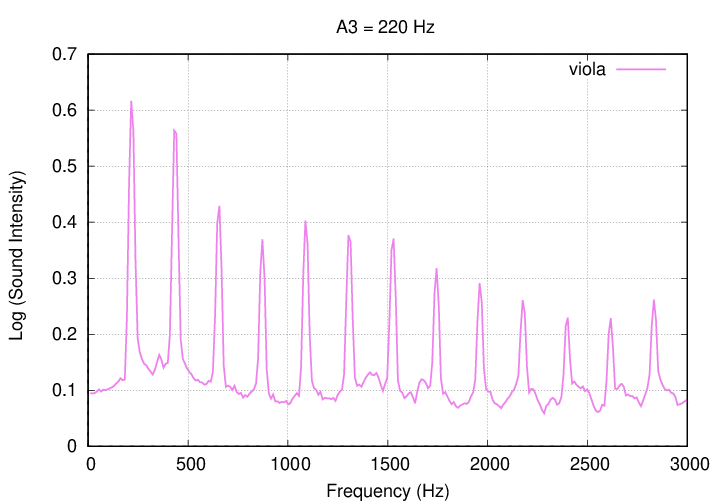
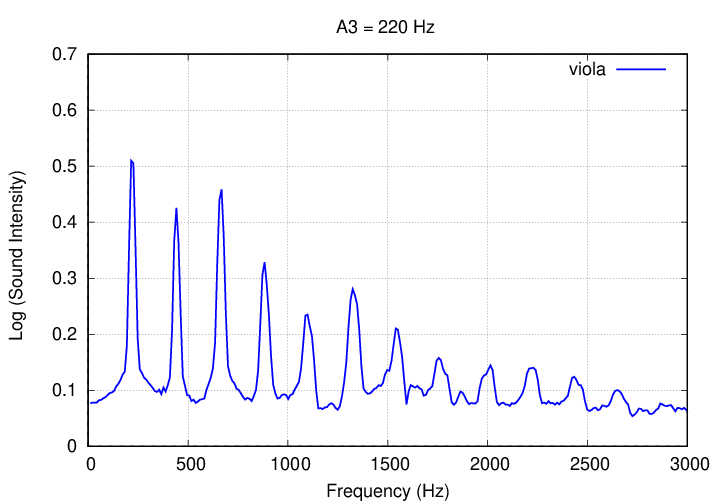
Some real instruments have a pattern of harmonics which is relatively smooth and simple; the viola, for example.
The flute, on the other hand, has a much stronger second harmonic (at 660 Hz) than first harmonic (at 440 Hz).
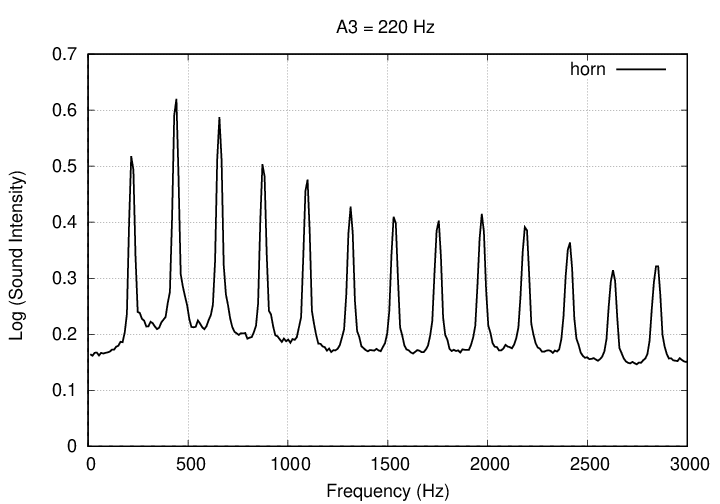
When the horn plays an A3, the amplitude of the first harmonic is even stronger than that of the fundamental. After that, though, the higher harmonics appear to decrease relatively smoothly.
The piano is just a mess. Yes, this really is a 220-Hz A3 -- but the fundamental is just the SIXTH-strongest of the frequencies! Note that some of the frequencies have "shoulders," too.
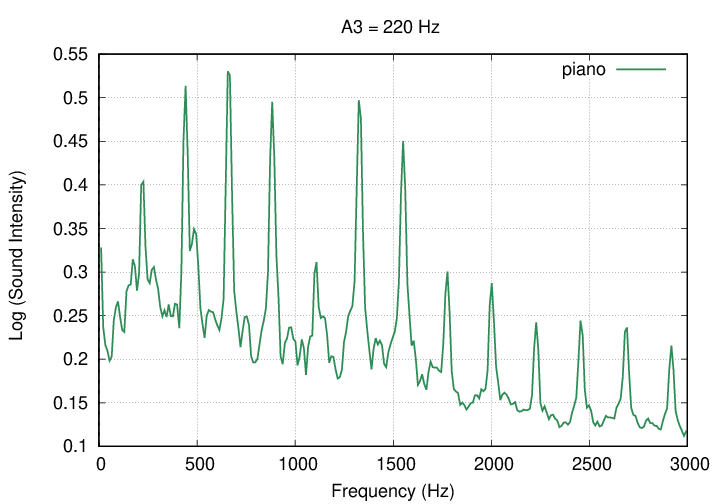
The complex spectrum of the piano's sound is due in part to the more complex mechanical structure of the instrument. It has several sets of strings, pulled taut across a steel frame, sitting on top of a wooden box with long legs. All sorts of vibrations can be excited when a hammer strikes one of the strings.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.