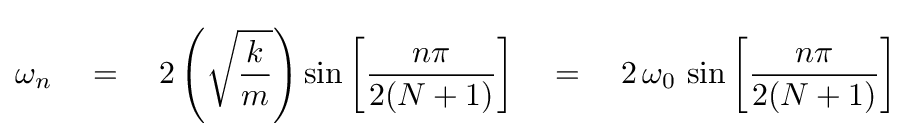
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Executive summary:
We can use the methods we've developed for dealing with
multiple masses connected by ideal springs
to figure out the behavior of a long, thin string
stretched between two pegs.
If we break that string up into lots of little segments,
and consider the forces exerted on each segment by
its neighbors,
we can derive two important features of oscillations
of the entire string:
These two conclusions should be very familiar to you, since you saw them back in UP I
Today we also will go through the process of deriving a relationship between the frequencies of the normal modes of oscillation in a system with many springs, and the index of the modes. You may recall that in the recent past, I simply stated that this relationship existed ...
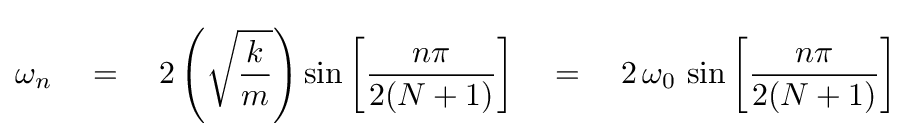
... and promised that I'd justify it later. Well, here we go!
Today, we begin to turn our attention from vibrations to waves. Vibrations are periodic oscillations which take place in a fixed position, but waves are disturbances which can propagate from one place to another. However, if one looks at a wave in the right way, one will see a set of many oscillators, each vibrating in place; the overall position of each one is fixed. So there's a close connection between these phenomena.
We'll begin by considering the vibrations which might take place along a string ... but eventually see how those vibrations can turn into waves along the string.
Just as a reminder, here is some information on the normal modes of a vibrating string that you ought to recall from University Physics:
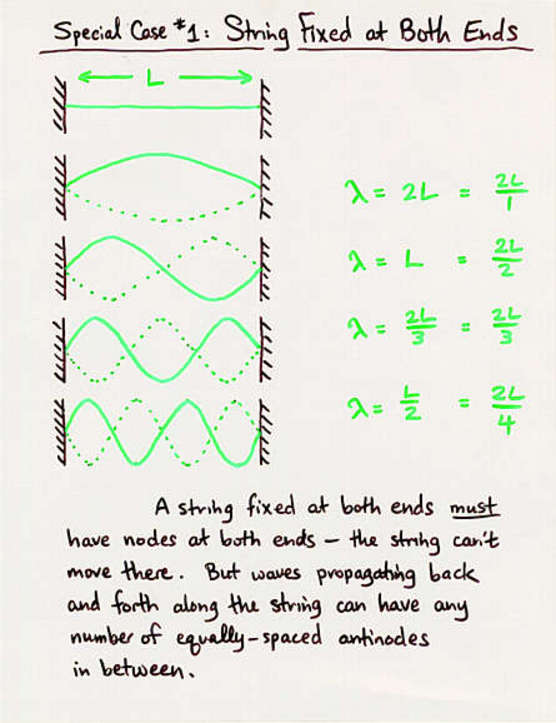
Note that there are many possible solutions, not just one.
Let's tie two ends of a string to fixed posts, then tighten the string so that all portions of it experience the same tension T. We will assume that this tension is identical at all locations throughout the string.
If we displace the middle of the string upward, and then release it, the string will vibrate up and down, up and down. The amplitude of the motion will be largest at the center, and must be zero at each end.

This string is a continuous medium, but we can approximate it as a number of tiny point masses, connected by ideal springs. If we use only one mass, the approximation is bad,

but if we increase the number of masses, it grows more accurate.

Eventually, we will allow the number N of masses to grow very large, and approach infinity. Let us call the mass of each tiny segment m, and the length of each tiny segment L.

Our goal is to figure out an equation which will allow us to write the vertical (y) position of each little piece of string, at any horizontal location (x), at any time.
Let's assume that the number of pieces is pretty large: N = 100 or N = 1000 or so. We'll pick just three segments, somewhere in the middle of the string, and focus in on their properties.

Let's zoom in, and examine the forces acting on the p'th little block. It is being pulled down-and-to-the-left by block p-1, and pulled up-and-to-the-right by block p+1.

At this point, we make the additional approximation that all vertical motions are small compared to the horizontal length of the string. That means that the vertical displacements in the diagram above should be small compared to the horizontal distance between the blocks. In other words, we are assuming that the angles θ are all small.
So, if we focus on the vertical components of these two forces on block p, one pulls down, and the other pulls up. In each case, the vertical component has a factor with the term sin(θ) in it.

And, strictly speaking, the sine of that angle involves the ratio of the vertical distance between the two blocks to the diagonal distance between them -- which looks like a mess.

But, as long as these triangles are long and skinny, so that the angles are small, then there is an approximation which makes the analysis much simpler.
If the length of the vertical side is much smaller than the length of horizontal side, then the sum of the SQUARES of those two quantities is -- to first order -- just the square of the first; and that means that the length of the hypotenuse is approximately L.

Thus, we can write the sine of the angle in a simple way.

And so the expression for the force in the y-direction on the p'th section of the string is

Replacing the force by mass times acceleration, and then moving the mass to the right, we have a differential equation for yp -- but it involves factors of yp+1 and yp-1 as well.

In other words, we have a COUPLED differential equation for each section of the string. The coefficients in front of these terms might look familiar, if you recall our analysis of the old "3-block, 4-spring" systems.
So, we have a coupled differential equation, involving the properties of three adjacent sections of the string. What we want is some equation which gives the y-position of the string, at any x-position, and at any time.

But how can we find the equation which satisfies our differential equation?
Well, one approach is to GUESS. Let's guess that there are normal modes to the string's motion, in which all sections oscillate with the same frequencies. Our guess will be that each section moves up and down like a simple harmonic oscillator:

The real challenge here will be in figuring out the amplitude Ap of the p'th segment's motion ... but we'll come back to that soon.
Given this guess, we can easily take the second derivative and plug it into our differential equation:

Divide both sides by the cosine term

and then put all the terms with Ap on the left.

Now, remember, all of this is based on our guess for the equation of motion of each segment. In order for it to be true, we need to make sure that the amplitude of motion of each little piece -- the A terms -- satisfy this equation.
It will help if we re-arrange it just a bit more, so that all the A terms go on one side and everything else on the other:

Note that all the terms on the RIGHT-hand side are constants; that means that the entire right-hand side must be some value which is the same, regardless of the particular section p of string we are measuring. If the right-hand side is a constant, then that means that the LEFT-hand side must be a constant, too.
This is a fine puzzle: we are trying to figure out the amplitudes of motion of each little section of the string, yet all we have is the information that one particular ratio of the amplitudes of the neighbors of a section, to the amplitude of the section itself, is constant.
No, that's not quite right: we also have two boundary conditions. We know that the amplitudes of motion of the sections at the end of the string must be zero -- because they are tied to fixed posts.

Note that on the left-hand side of the string, the amplitudes are INCREASING, so Ap+1 > Ap > Ap-1 ,

while on the right-hand side of the string, the amplitudes are DECREASING, Ap+1 < Ap < Ap-1 ,

and yet, for all regions of the string, this ratio must be identical.
How can we arrange the amplitudes of each piece so that all this is true?
Well, suppose that we pick some teeny little angle α. Let's say that the amplitude of the first segment of string, next to the left-hand post, is equal to some constant times the sine of this little angle. That should yield a very small amplitude of motion -- which is good, because this string is right next to the post.

The amplitudes of the next sections should be bigger, so let's try using multiples of the angle α to compute them. As the argument of the sine function grows, the size of the result will grow, too.

In general, let's guess that the amplitude of the p'th section of the string is based on the sine of p times the teeny angle α. The constant C is simply the maximum displacement of the string, at the midpoint, between the posts.

Now, one good reason to choose this funny-looking expression for the amplitude of the p'th section of the string is that the sine function produces values which
but then, after p reaches a particular point, the sine function values
With this guess, the constant ratio of amplitudes becomes

Now, this is somewhat complicated, but we can simplify it if we make use of the following trig identity (the first of two which we will pull from the mists of time in this procedure):

Using this identity, the numerator on the right becomes

and thus the requirement for the ratio of amplitudes simplifies to

The term on the left-hand side is supposed to be a constant, independent of the segment p ... and the term on the right-hand side is definitely a constant. That all checks out. Good!
We have almost reached the end of our journey: if we can just figure out the value of the teeny angle α, then we will finally be able to write the amplitude Ap for every section of the string. But what is this angle?
Perhaps the boundary conditions will help. The first boundary condition is that the amplitude at the left-hand post, at p = 0, must be zero. That gives us

Well, that doesn't help at all. The sine of zero is zero, regardless of α.
The other boundary condition is that the amplitude at the right-hand post, at p = N+1, is also zero.

Q: What does this tell us about the angle α?
This is VERY helpful. It tells us that the angle α must be just the right size so that (N+1) times α is a multiple of π -- because the only zeroes of the sine function are at multiples of π.

And so we see that there are a series of values for the teeny angle α which will satisfy all the requirements:

Finally, we know the amplitudes of motion for each little section of string. There are a number of choices, depending on the value of the integer n -- which is good, because we need to be able to write down a number of solutions, each with a different wavelength and frequency.

And that means we can write down the vertical position of any little segment of the string, at any time.

Great. We know what the AMPLITUDES of each little section of the string are for the normal modes -- but what about the FREQUENCIES of motion?
We can find them by putting together two pieces of the puzzle we have derived earlier. When we were investigating the amplitudes of the normal modes, we found that the ratio of amplitudes of adjacent sections was related to the frequency of oscillation like so:

But we also found that this same ratio was equal to twice the cosine of the angle α

Since we know what α must be, we can set these two expressions equal to each other, and then solve for the frequency associated with each value of n.



Q: Do the units match on both sides of this equation?
We could stop at this point, but let's make one final adjustment. This expression has a term like [1 - cos(x)], and there's a trigonometric identity that will allow us to convert that into an expression involving the sine function instead:

So, if we define
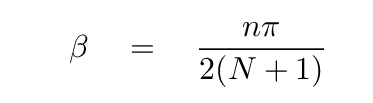
then we can write the expression for frequency-squared as

And so the frequency of the n-th normal mode is given by

Hmmm. That factor inside the square root looks sort of, kind of familiar. You might recall that the speed of a wave travelling along a string is given by

Q: Is the expression for ω equal to the expression for velocity
(ignoring the sine term)?
Q: How are the two related?
This was a lot of math, but it's just one way to show a result that you've seen before.
Just take a peek at these notes and pictures from University Physics; don't they look familiar? Below are the two most relevant viewgraphs from that lecture.


 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.