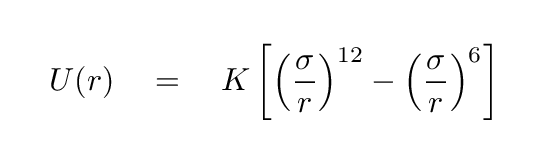
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
There are two reasons that we spend so much time on SHM in physics and other sciences.
The first reason is one of convenience. Objects exhibiting SHM move in simple ways, which can be calculated easily and quickly with nothing more than a calculator. Moreover, the relationship between several properties of an object -- its position, velocity and acceleration -- are also easy to compute. This simplicity means that even if SHM may not describe the behavior of an object perfectly, scientists will often adopt it as a quick-and-easy approximation.
And we're lucky: as we will see in a moment, there are many, many, MANY circumstances in the physical world in which the conditions are present for SHM to occur. A short, very partial list of them will show this wide range of environments:
What do all these (and many other) situations have in common? The key is a stable equilibrium, often between opposing forces. There are several ways to describe this mathematically. One involves the description of potential energy as a function of the position of an object. If the potential energy as a function of position contains a minimum, then that location is a stable equilibrium: an object placed at that location, and then nudged slightly in any direction, will return to the point of equilibrium.
Consider the graph of potential energy shown below, which features a "Lennard-Jones" potential
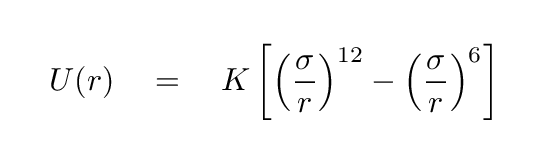
For simplicity, let's set the values of the constants K = 1 and σ = 1.
Q: What is the location of the minimum in this curve?
Now, what connection does this have to SHM? The key is that SHM will occur whenever the potential energy around some minimum has the form of a quadratic function of the displacement.
Q: Does the Lennard-Jones potential look like a quadratic function?
Well, no. But what if we zoom in a bit?
Does the graph look like a parabola now?
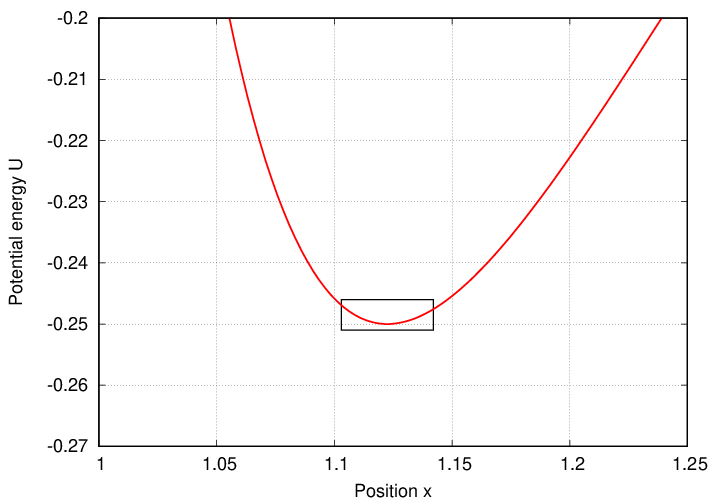
What if we zoom in again?
It appears that if one considers only "small" displacements from the equilibrium location, then some -- maybe even most -- potential energy functions may take on quadratic-like forms. The question "how small must the displacements be?" is a very important one; one must deal with each particular situation carefully to figure out the limits of this approximation.
We can put some mathematical justification behind the claim that potential energy functions will take on quadratic forms for "small" displancements around the location of a stable equilibrium. Recall that one can express the value of a function f(x) near some particular value x0 as the sum of a series of terms involving the derivatives of f(x) around that position.
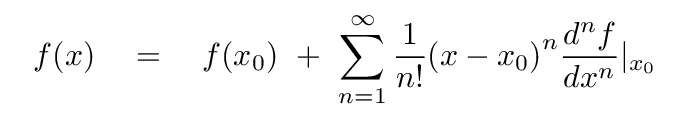
Now, if the point x0 in question happens to be a local minimum (and hence a stable equilibrium), then by definition, the first derivative is zero. That means that we can compute values of the function near this location like so:
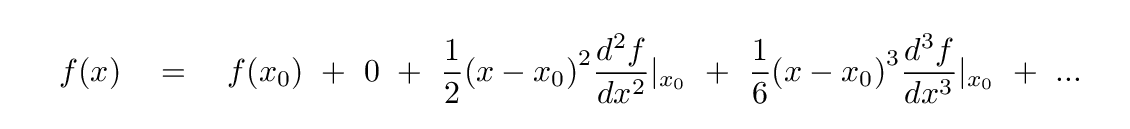
If we agree to move only a "small distance" away from the equilibrium, so that (x - x0) is a "small" quantity (remember, we must be careful to determine the distance which counts as "small" in each instance), then we can keep only the leading term in the series:
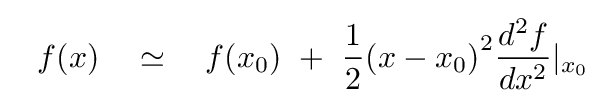
Rewriting this result, it becomes clear that this function really does look quadratic -- as long as displacements are "small" enough.
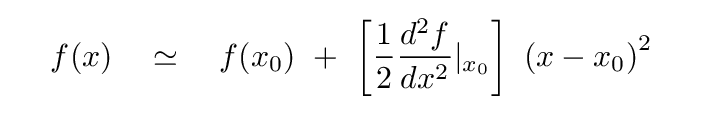
There are times when it is more convenient to describe a situation using forces than using potential energy. Let's see how to convert our description of an object moved slightly away from a stable equilibrium in terms of forces.
Suppose we have some potential energy function U(x). In the neighborhood of a stable equilibrium, we can approximate the value of potential energy as
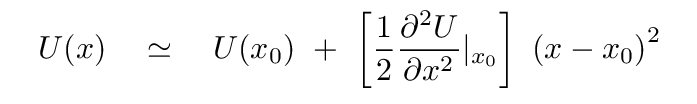
There is a force associated with any potential energy function, which is related to it like so:
So, let's take the derivative of the potential energy function.
... and so, we can substitute in the force (as long as we don't forget the negative sign):
All that stuff in the square brackets is some constant value, so we can replace it with a constant factor; let's call it K.
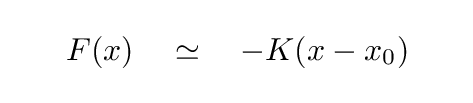
This ought to look familiar. If we displace an object from a stable equilibrium, we find a force which acts to restore the object to the equilibrium location -- a restoring force. This is another sign that the object will undergo SHM.
Let's pick some concrete system and use it as an illustration. Suppose that a small ball of mass m is placed in a little dip in the ground. If placed at the very bottom of the dip, it will sit motionless; but if we move it a bit to one side, it will experience a force pushing it back toward the bottom.
Let's simplify our notation a bit. We'll agree to make only small displacements, so we can replace the "approximately equal" sign with a regular equal sign. In addition, we will shift the origin of the coordinate system to the point of equilibrium x0, so that the term (x - x0) becomes simply (x - 0) = x.
The force on the ball, F, is related to its mass and acceleration by Newton's Second Law. So we can write
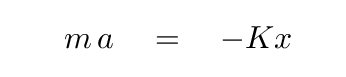
The acceleration of the ball, of course, is just its second derivative of position with respect to time, so
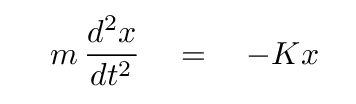
If we re-arrange,
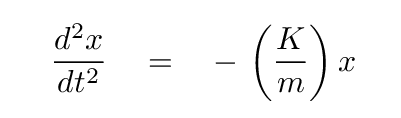
and then define a new quantity
Q: What are the units of ω?
then we can put the equation of motion into a standard form:
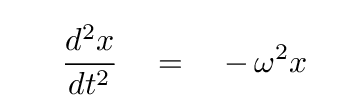
One can write the general solution to this differential equation in many different ways.
Q: What is one way to write the solution to this equation,
using a single cosine term?
Q: What is another way to write the solution to this equation,
using both a sine and cosine term?
Right. Two common ways to write the equation of motion of the ball are
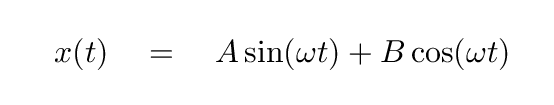
Joe builds a mini-golf course for nerds. The fifth hole has a long fairway with a series of dips and rises, so that the height of the course follows a perfect cosine function.
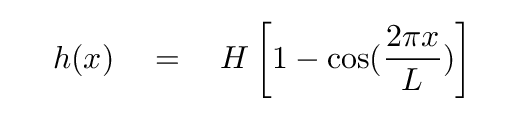
where
H = 0.2 m
L = 5.0 m
Viewed from the side, the course has an undulating appearance.
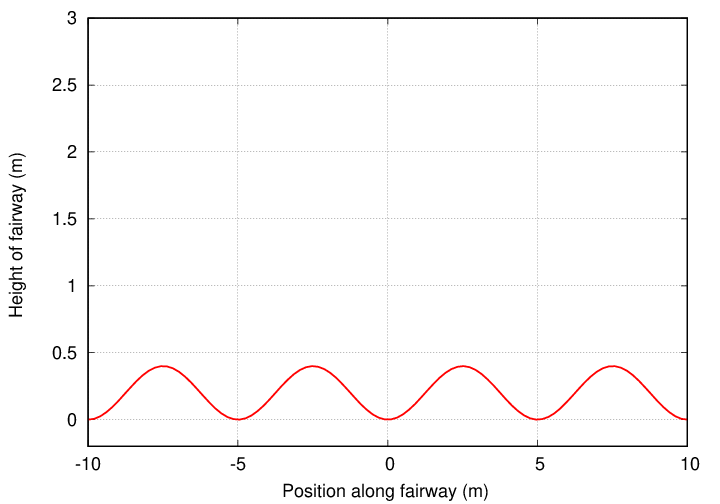
Suppose that a golf ball gets stuck in the "valley" in the middle of the course, at x = 0.
Q: If the ball is nudged a small distance to the side,
and the released, will it exhibit SHM?
Justify your answer.
One way to show that the ball would exhibit SHM is to verify that the potential energy has a quadratic form around its equilibrium point. Let's take a look.
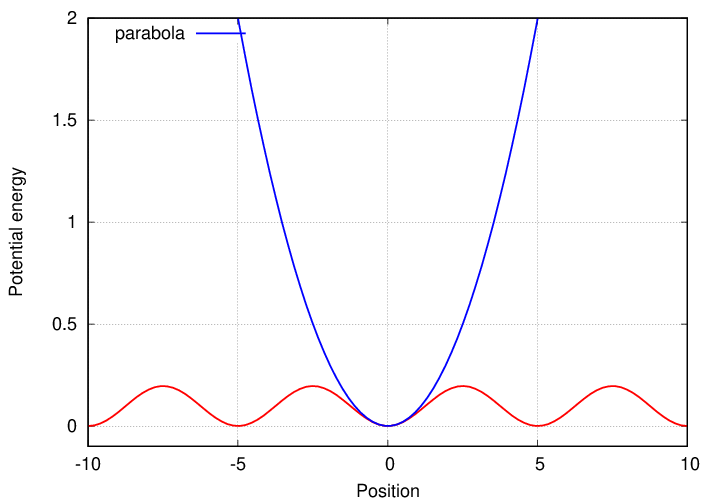
Q: If the ball is moved 3 meters to the right,
will it oscillate around the origin?
Q: What is the range of displacement which might
yield SHM?
Let's zoom in for a closer look:
Q: If the ball is moved 1.5 meters to the right,
will it oscillate around the origin?
Q: Will that oscillation be SHM?
Q: What is the range of displacement which might
yield SHM?
Maybe we should move in even farther.
Great! Displacements on scales of this size, around 0.2 or 0.3 meters, seem to be "small" enough.
Q: How many radians, θ, in its cycle corresponds to a
horizontal displacement of 0.3 meters?
Q: What is the sine of this angular displacement θ?
Q: Compare the angle θ to sin(θ)
We can perform the same analysis by examining the forces on the ball near the equilibrium point.
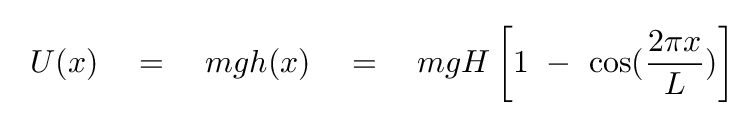
Q: What is the force, F(x), associated with this potential energy?
If we plot the force over a wide range of displacements from the equilibrium point, it doesn't look linear.
But if we zoom closer to the point of equilibrium, the force comes closer to a linear function.
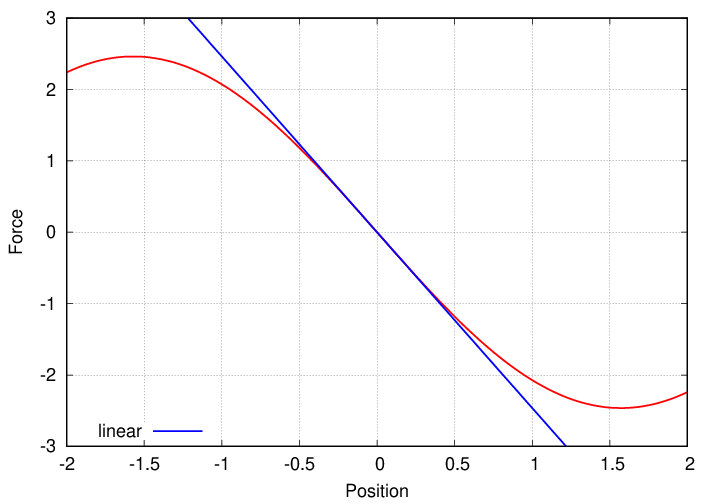
And for "small" displacements, it is very close to the linear form required to yield SHM.
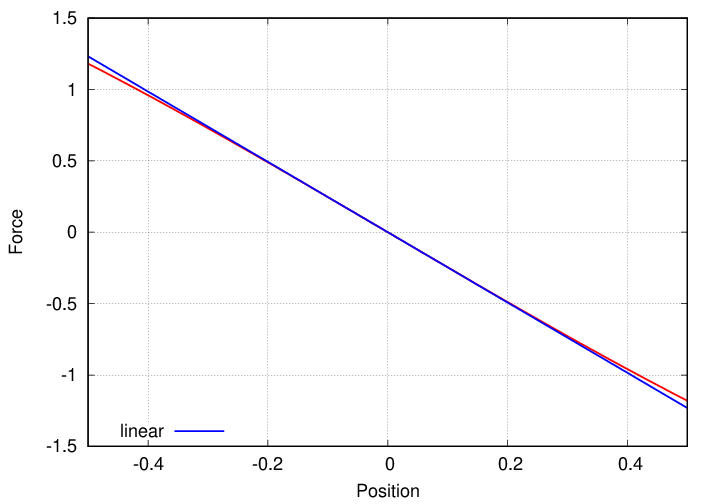
Q: If the golf ball is displaced by a sufficiently small
distance from x = 0, it will roll back
and forth in SHM. What is the period of that motion?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.