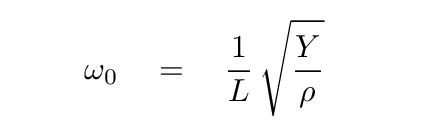
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Last time, as you may recall, we treated molecules in a salt crystal as if they were N identical blocks in a very long line, all joined by identical springs. Clearly, this is a rough approximation.
We guessed that the angular frequency of oscillations of atoms in the crystal would be roughly
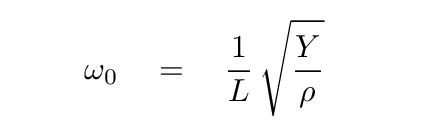
where
Y = 40 GPa
L = 0.28 nm
ρ = 2164 kg/m^3
Using this approximation, the angular frequency ω0 has a value of about 1.5 x 1013 rad/s. The corresponding frequency, in Hz, is
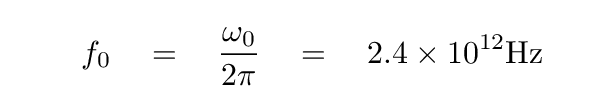
which lies in the terahertz range. The corresponding wavelength
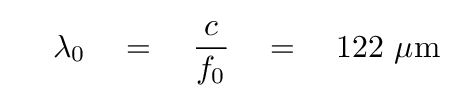
lies in the far infrared.
Now, the angular frequency of the normal mode with the highest energy -- when the index n = N -- is just twice this characteristic angular frequency. You can look at the section on 'many' coupled oscillators in our previous lecture to find the derivation. This most energetic mode should have the highest frequency, and therefore the shortest wavelength.

Q: What is the shortest wavelength at which light should be
absorbed or emitted by a salt crystal?
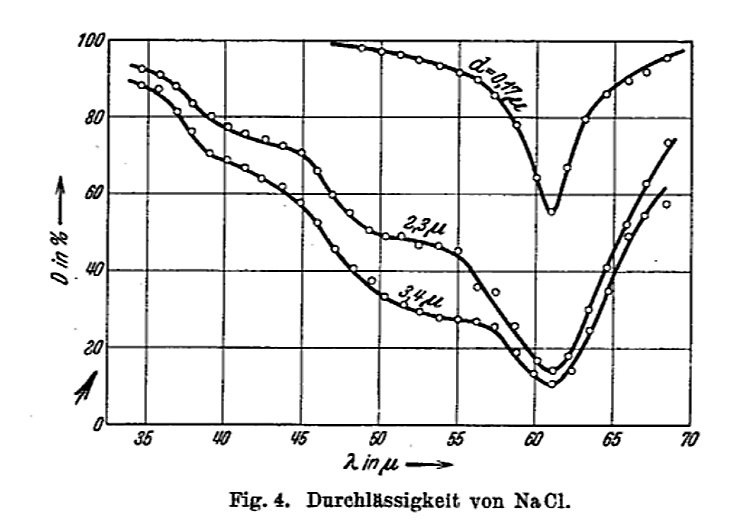
Figure 4 taken from
Barnes, R. B., Z. Physik, 75, 723 (1932)
As long as we are making rough approximations, we can turn this problem around. Based on the observations of this absorption of light, we KNOW that the angular frequency of oscillations inside the salt crystal is roughly
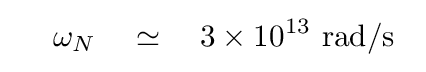
Let's try to estimate the "force constant" of the bonds between neighboring atoms in the crystal. Of course, the crystal is NOT a long, one-dimensional object, nor is it made of identical items (since sodium and chlorine atoms are different). But perhaps our attempt will show us the order of magnitude of the strength of these bonds.
Let's pretend that
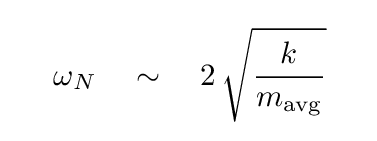
where the "average" mass is halfway between that of sodium (23 times mH) and chlorine (35.5 times mH).
Q: Given
ωN = 3 x 1013 rad/s
mavg = 5 x 10-26 kg
what is the force constant k in the crystal?
How does that compare to the force constant of the springs you have used in your lab classes?
Let's move from a solid to a gaseous substance, and see how well our oscillatory knowledge may help us to understand its properties. Consider a molecule of carbon monoxide:
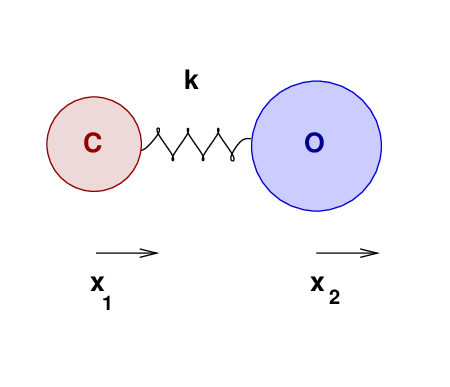
The two atoms have some equilibrium separation, when the molecule is in its ground state. When the molecule is given energy, the atoms may vibrate. We'll call the displacement of the carbon atom from its equilibrium position x1, and that of the oxygen atom x2.
As the atoms move, and their separation changes, they will experience forces due to the bond between them. Let us approximate that bond as an ideal spring of force constant k.
Can we figure out the frequency and wavelength of radiation emitted (or absorbed) by this molecule, due to changes in its vibrational state?
A good first step would be to write down the forces on each atom.
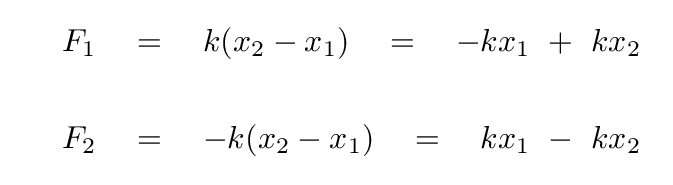
Before we go farther, we need to watch out for one tricky aspect of these equations: the masses of the two atoms are not the same, which means that there is a different factor in front of the acceleration of each atom.
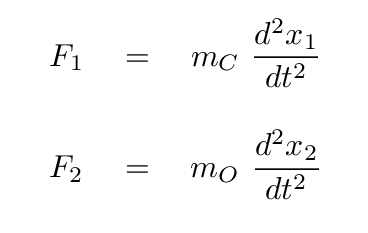
Q: What are the relative masses of a carbon and oxygen atom?
We can use this to express all masses in terms of either atom; how about oxygen?
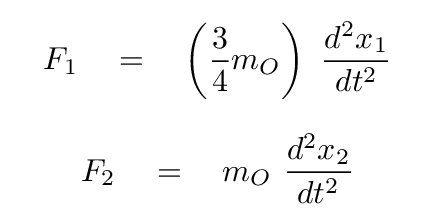
Now, putting these terms into our equations for the forces on each atom, we have
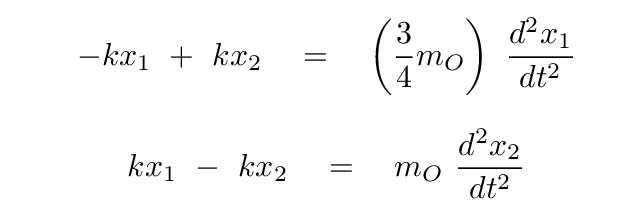
Okay, time for you to take a turn: please convert these two equations into a single matrix equation, in which we assume that there is some linear combination s = a x1 + b x2 of the positions which yields SHM. In other words,
Q: Write out the matrix form which allows us to compute
the eigenvalues of this system.
Now, to solve for the eigvenvalues of this equation, we begin by writing out the equation based on the top row of the matrix.
Solve for b in terms of a, so that we can eliminate it.
Plug this expression for b into the equation based on the second row of the matrix, and, after some algebra, you should see
How nice! Some of these terms will cancel.
Q: What are the values of ω which satisfy this equation?
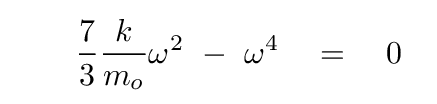
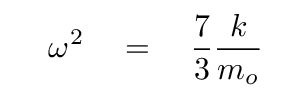
Phew. That wasn't so bad.
Now, if we could measure the angular frequencies of actual vibrational transitions from the ground state to the first excited state of CO -- from n=0 to n=1 -- then we could estimate the value of the "force constant" binding together the two atoms.
Well, others have measured the properties of this transition. The graph below shows the wave number of the photons absorbed (or emitted) by the transition. The wave number is simply the frequency divided by the speed of light, f/c.
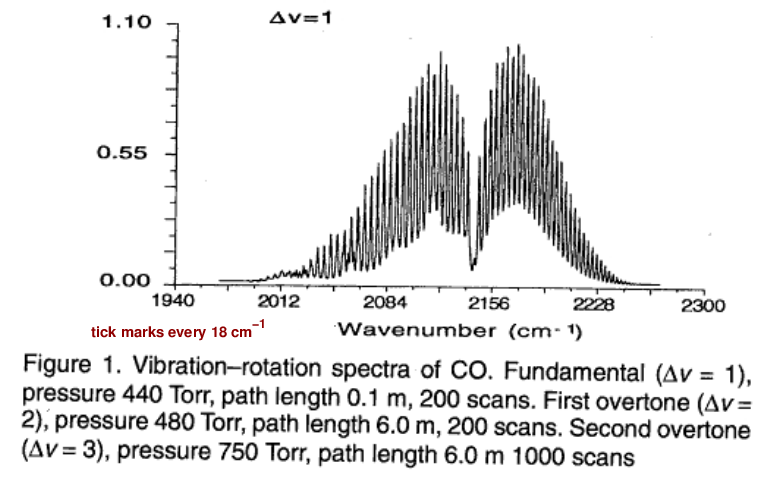
Figure 1 taken from
Molecular Constants of Carbon Monoxide at v=0, 1, 2, and 3
by Mina-Camilde, Manzanares, and Caballero,
Journal of Chemical Education, 73, 804 (1996)
Q: Estimate the wave number from this graph. Q: Use the wave number (f/c) to compute the frequency f (in Hz). Q: Then compute the angular frequency ω (in rad/s).
You should find the angular frequency is close to ω = 4.0 x 1014 rad/s.
The mass of an oxygen atom is just 16 times that of a hydrogen atom, or about 16 times that of a proton.
Armed with this information, and the equation we just derived for the angular frequency
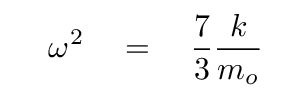
you can now estimate the force constant of the bond between the two atoms.
Q: What is the force constant of the "spring" between C and O?
I found a value of k ≈ 1900 N/m. Did you?
This seems to be quite a bit stronger than the force constant of the bond between neighboring atoms in a salt crystal. Can you think of any reasons why this might be?
Why stop at one oxygen molecule? Carbon dioxide has not one, but TWO carbon-oxygen bonds.
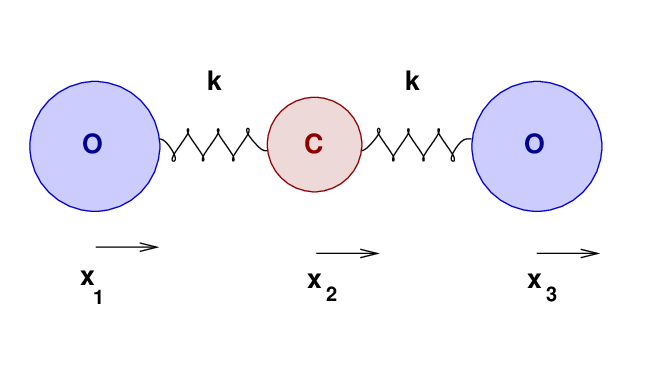
A naive approach would be to assume that the force constant k of each C-O bond in in CO2 is exactly the same as it is in CO.
Q: What do you think?
a) "k" in CO2 is larger than in CO
b) "k" in CO2 is same as in CO
c) "k" in CO2 is smaller than in CO
Well, let's make this assumption, and see where it takes us. Perhaps we'll be able to find out if we are right.
Q: If we want to find out the frequencies with which this molecule
can vibrate, what would a good first step?
Did you say, "Write down the forces on each atom?" If so, have a cookie.

These may have been the first chocolate-chip cookies
baked in the kitchens of restaurant Nagomi (Agematsu, Japan)
Ahem. Back to physics.
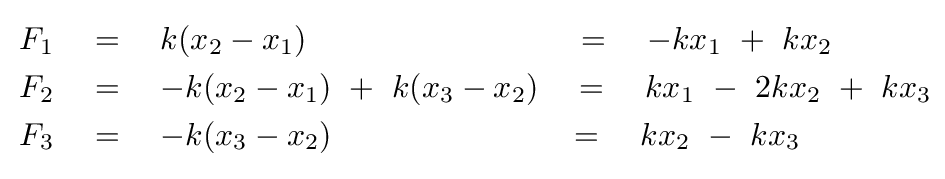
Once again, the fact that the "blocks" in the molecule have different masses means that we must be very careful as we convert these equations into the standard matrix format.
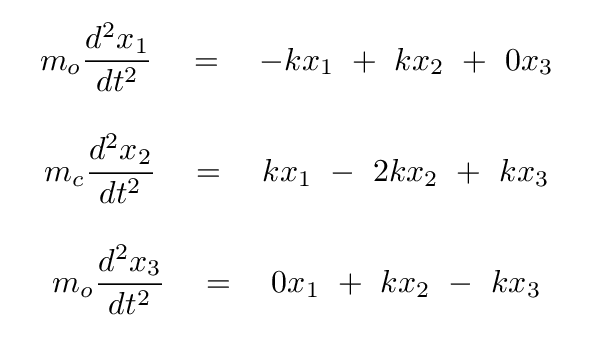
Q: Write these in the form of a single matrix equation.
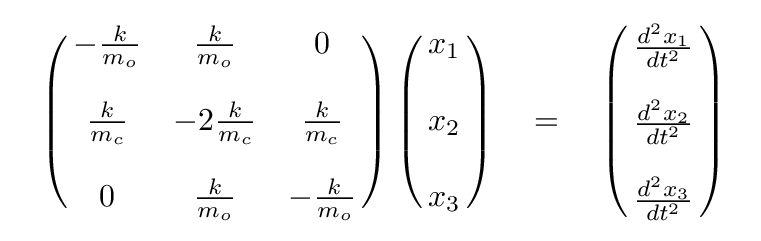
Once again, we can simplify, using the ratio of masses
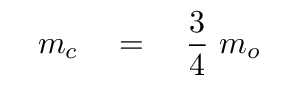
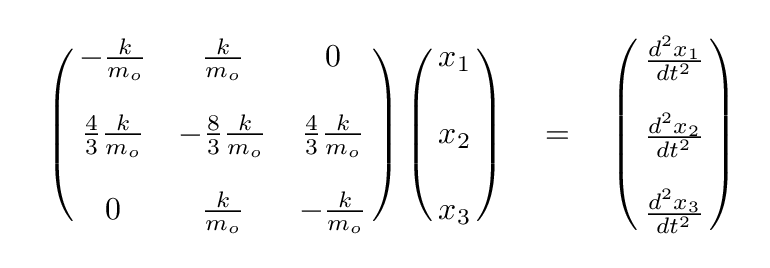
It looks even less crowded if we factor out the ratio of k/mo.
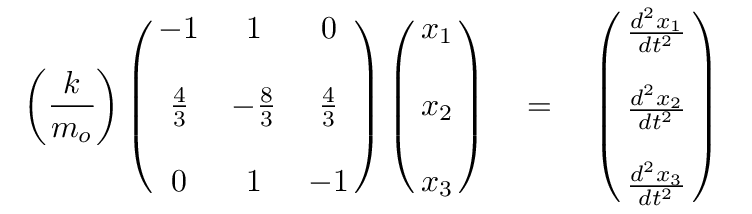
Q: Can you write the eigenvalue version of this matrix formula,
assuming that a linear combination of the positions
of the atoms will yield SHM?
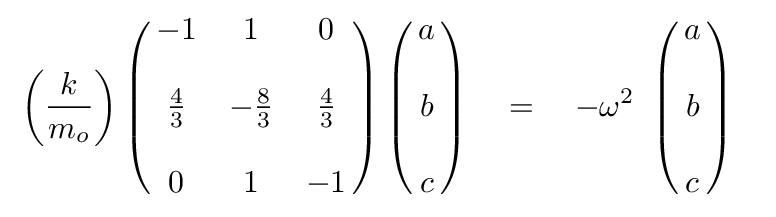
At this point, we can turn to a linear-algrebra or matrix math package and ask it to find the eigenvalues and eigenvectors. The results are eigenvalues of 0, -1, -11/3, corresponding to angular frequencies of
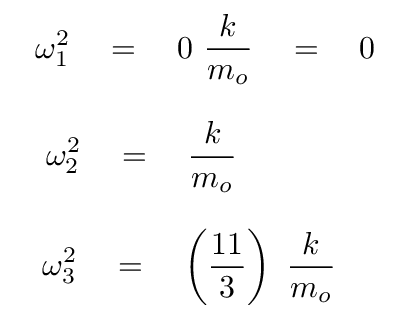
The first possibility isn't interesting -- no oscillations. Skip it.
The second eigenvalue has an eigenvector of
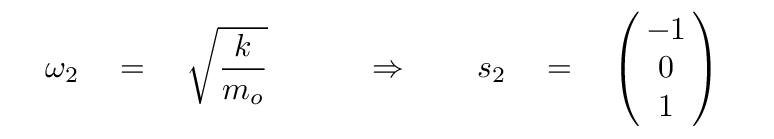
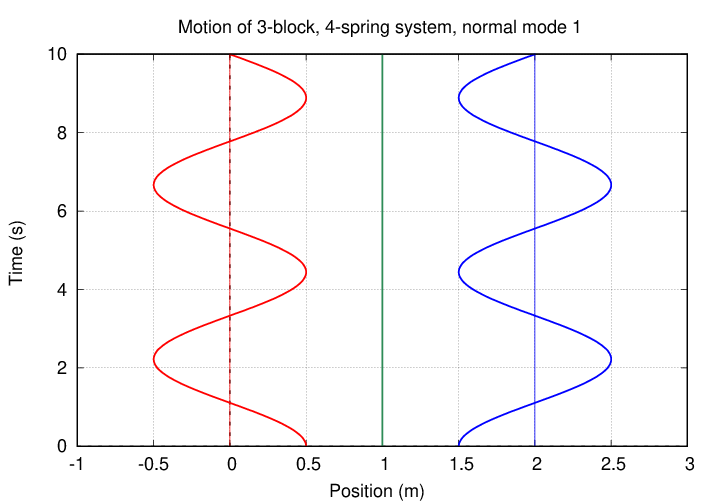
In this mode, the two oxygen atoms move by equal but opposite amounts, while the carbon atom in the center remains motionless. It's the same pattern as this one (from a slightly different problem):
Q: Assuming that the force constant between C and O is still k ≈ 1900 N/m,
compute the angular frequency of this oscillation.
Q: What would the wavelength of photon corresponding to a transition
from the ground state to this mode be?
Does real CO2 show any absorption at this wavelength?
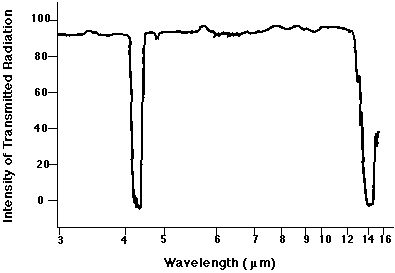
Figure 5 taken from
Infrared Spectroscopy
a part of
Yun Hee Jang's General Chemistry class
at CalTech.
No. There is no absorption line at 7.1 microns. Why not? Did we make a mistake?
No mistake. The reason that we see no absorption feature is that this sort of vibration -- with each oxygen atom moving by the same amount in opposite directions -- does not change the electric dipole moment of the molecule. The interaction of light with matter is strong when there are changes to the electric dipole moment, but very weak (or "forbidden") when no such change occurs.
Bummer.
But wait! There's one more frequency to consider:
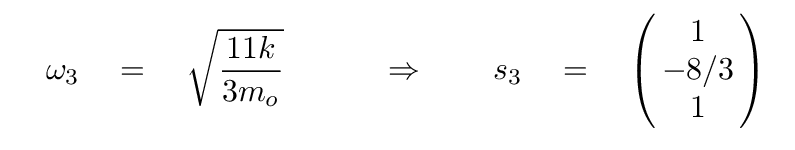
In this mode, the two oxygen atoms move by equal amounts in the same direction, but the carbon atom in the middle moves by a larger amount in the OPPOSITE direction. The pattern looks sort of like this (except that the central atom's amplitude of motion is larger):
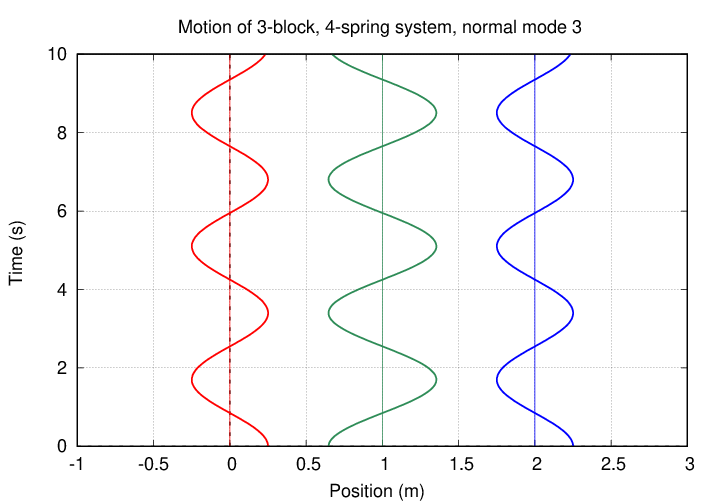
Now, this motion DOES change the electric dipole moment of the molecule, and so there IS a strong coupling to electromagnetic radiation. We really ought to see an absorption line due to the transition from the ground state to this type of vibration.
Q: Assuming that the force constant between C and O is still k ≈ 1900 N/m,
compute the angular frequency of this oscillation.
Q: What would the wavelength of photon corresponding to a transition
from the ground state to this mode be?
Does real CO2 show any absorption at this wavelength?

Figure 5 taken from
Infrared Spectroscopy
a part of
Yun Hee Jang's General Chemistry class
at CalTech.
Close! Our calculation suggested that the line ought to appear at λ = 3.7 microns, but there is a strong absorption feature at λ = 4.26 microns. That feature really is due to this mode of oscillation.
Q: Which of the following might explain the difference between our calculated
value of 3.7 microns, and the real value of 4.26 microns?
a) "k" in CO2 is larger than in CO
b) "k" in CO2 is same as in CO
c) "k" in CO2 is smaller than in CO
Can you come up with any reasonable justifications for the difference in the spring constant?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.