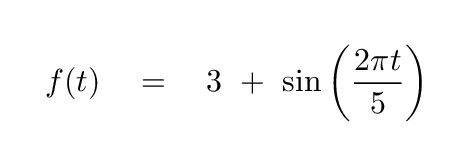
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The plan today is simply to work through two examples of Fourier analysis. We will determine the coefficients for the first few terms in the series describing two different periodic functions.
We'll begin with a function to which we know the answer -- always a good way to begin practicing a new technique. Our function will be
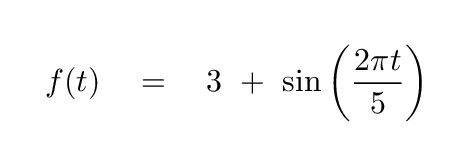
Q: What is the period of this function?
Since the general form of a sine or cosine function can be written
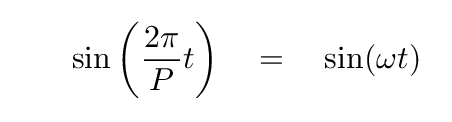
it's clear that the period of this function is P = 5 s.
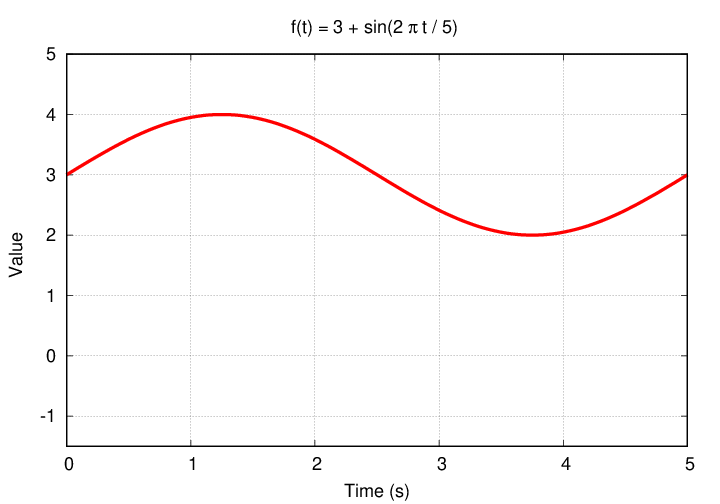
Our goal is to determine the Fourier coefficients which will represent this function.
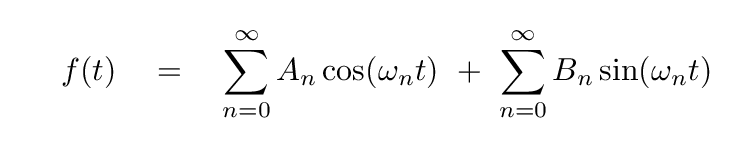
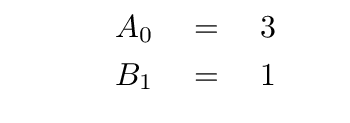
But let's go through the motions to make sure that we do end up with these values.
The n=0 case is pretty easy: the sine coefficient B0 is always zero, and the cosine coefficient A0 can be calculated via
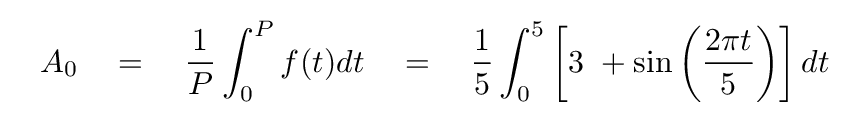
Let's split up the work. You do the first term of the integral, and I'll do the second.
Q: What is the result of integrating the constant term?
The constant term yields a value of 3.
The second half of the integral takes a bit more work. First, we perform the integration ...
Then we evaluate the result at the limits of integration
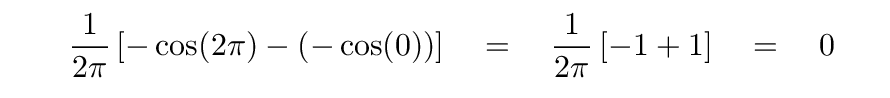
The sum of the pieces of the integral therefore is
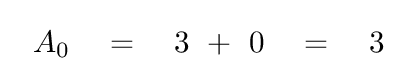
Okay. Let's see how well the n=0 terms of the Fourier series match the input function f(t).
Hmmm. They did their job: accounting for the average value of the function. The remaining terms in the series simply have to account for the variation around this mean value over one period.
Let's now move on to the n=1 terms in the series. We have
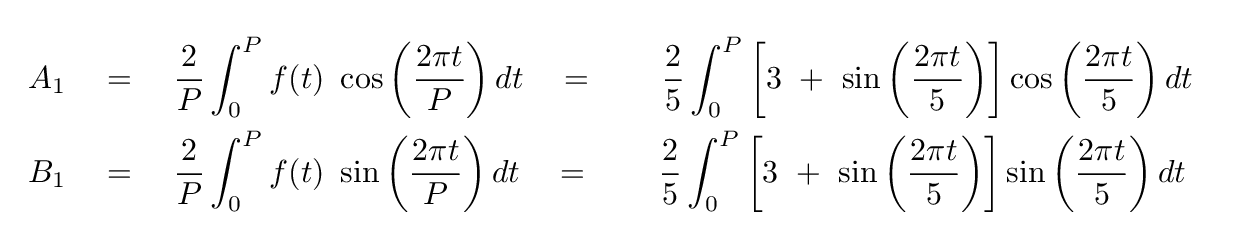
Let's take these one at a time. We'll begin with the A1 term.
Q: Which of the following statements is true?
a. both terms in this expression are zero
b. only the first term in this expression is zero
c. only the second term in this expression is zero
d. neither of the terms in this expression are zero
Aha. The second term involves an integral of the product of a sine term and a cosine term. Thanks to the orthogonality of our basis functions, such products will always yield an integral of zero. That means that we need only to evaluate the first term.
Excellent! Just as we expected,
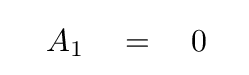
And it turns out that all the other A terms will also be zero.
Now for the second possibility: the sine term with coefficient B1.
We can integrate the first term as-is, but we'll need to perform a trig substitution on the second term.
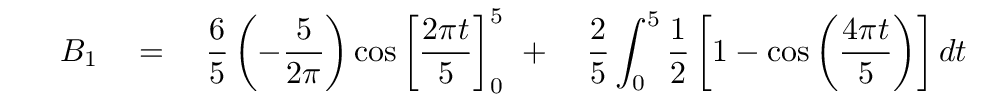
That second term now breaks into two simpler integrals.
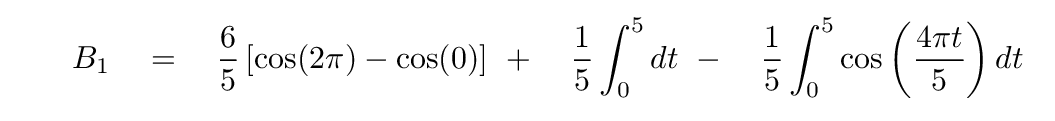
We can deal with the first two terms quickly, but the third term will take another line or two of work.
Voila! We were expecting B1 to have a value of 1, and so it does. Hooray!
If one goes through the motions for sine terms with higher values of n, one will find that they all equal zero.
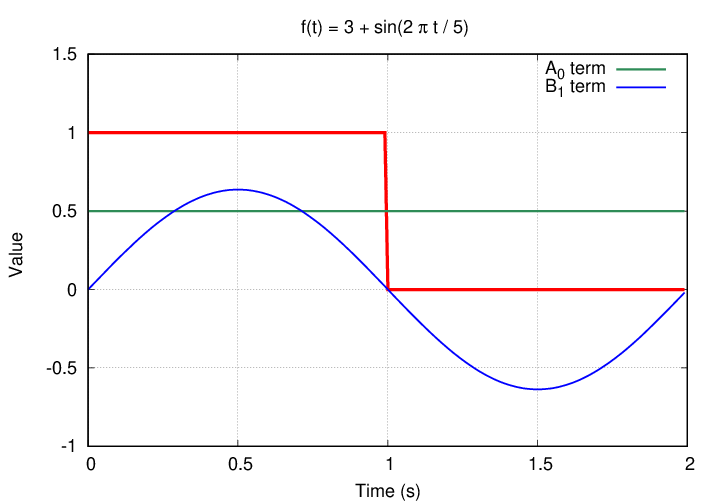
Let's see how our two non-zero terms in the Fourier series compare to the function we are trying to replicate.
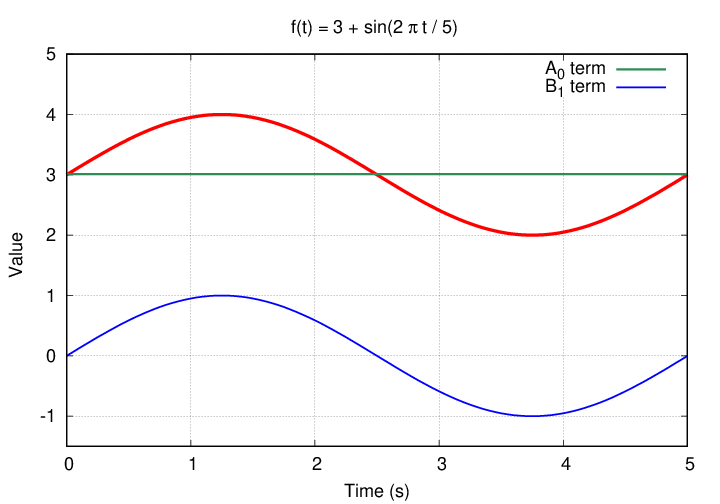
If we add them together, we do indeed match the starting function. Phew.
Let's try something more challenging: a square wave. What's that? It's a periodic function which alternates between two values. In our case, the two values will be 1 and 0, and the period will be P = 2 s.
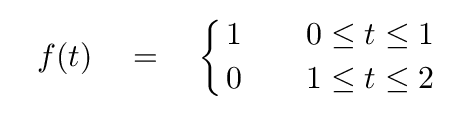
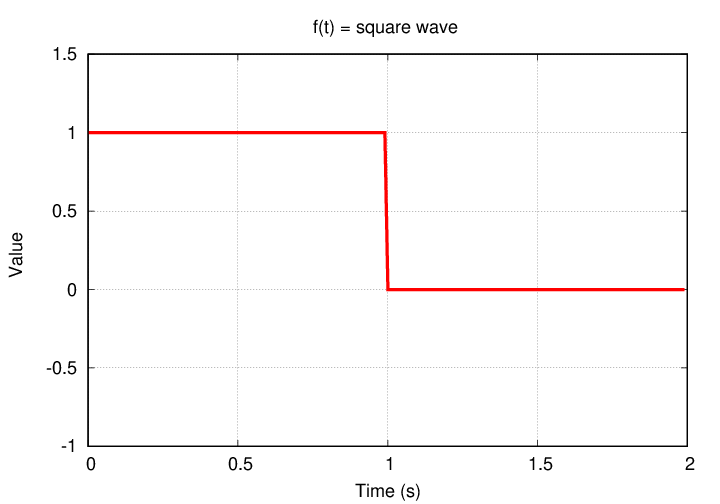
How can we put together a set of smoothly varying sines and cosines to yield such harsh, sharp angles? Good question. Let's find out.
Our first step is the n=0 terms. The sine term is zero, as always, and the cosine term is given by an integral which we can split into two pieces.
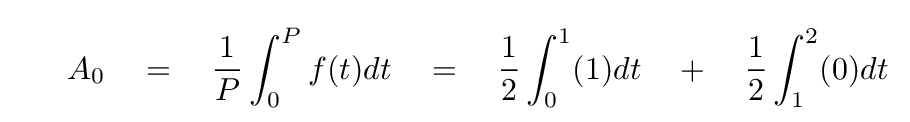
Q: What is the value of this coefficient A0?
That's ... just 1/2. So, if we include only terms up to n=0, our series approximation is
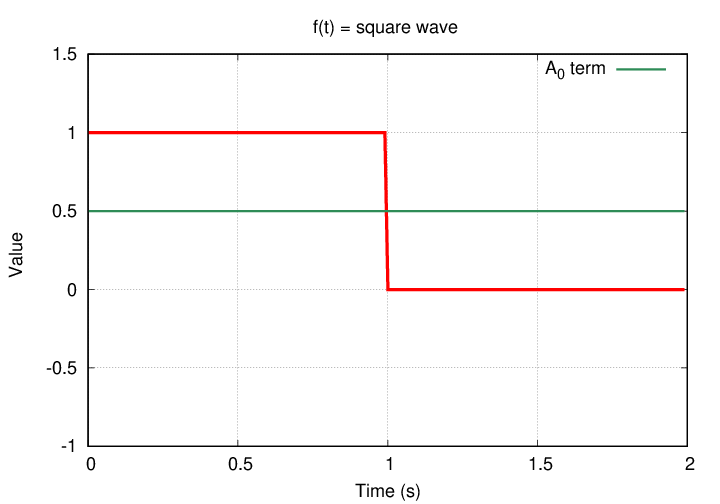
A promising start. Once again, the A0 term takes care of the average value of the function over one period, leaving all the higher-order terms to deal with the variations around this mean.
Next are the n=1 terms.
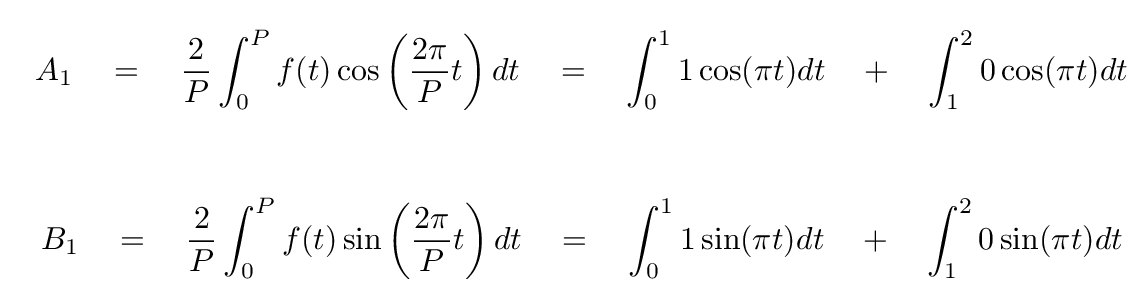
Q: What is the value of each coefficient?
You should find
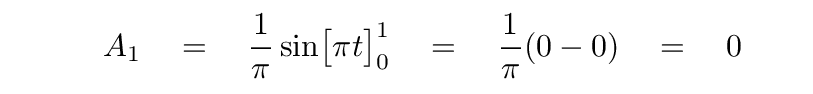
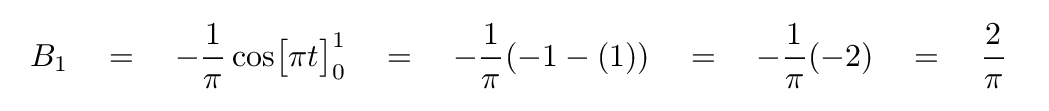
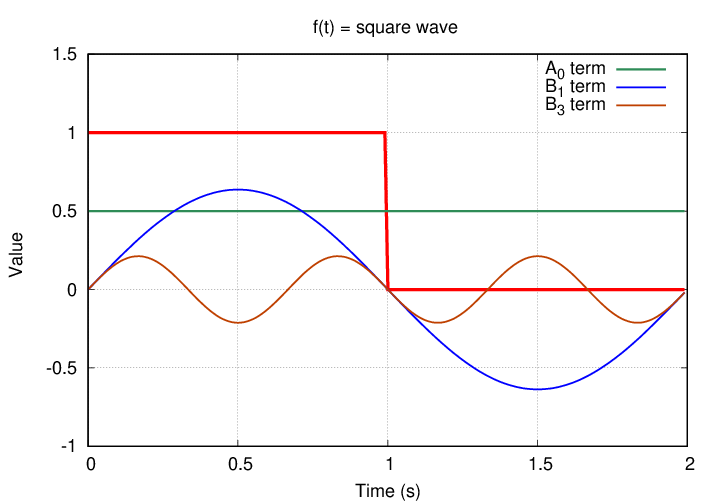
Our Fourier series now includes terms of order n=0 and n=1. How well does it reproduce the square wave?
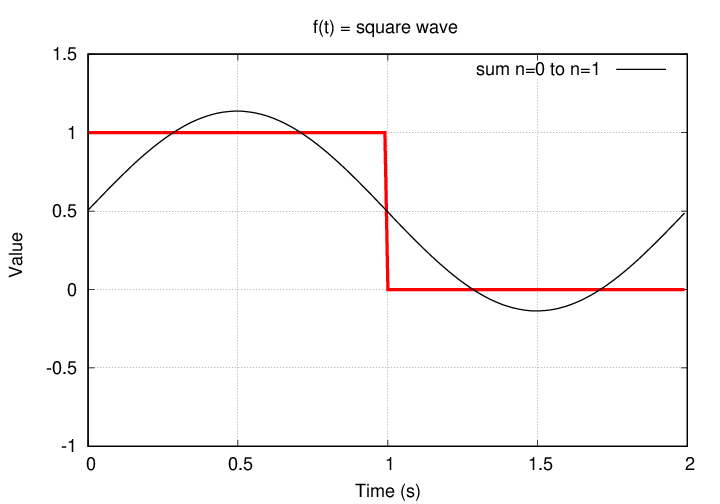
It's a start, but the corners aren't very sharp. Maybe adding some additional terms will help.
Let's try the n=2 ...
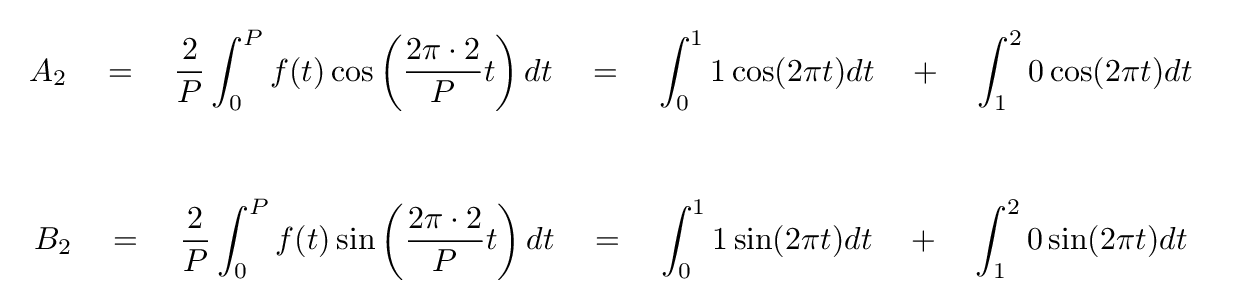
... and n=3 terms.
Q: What are the values of A2 and B2? Q: What are the values of A3 and B3?
You should find that both of the n=2 coefficients are zero,
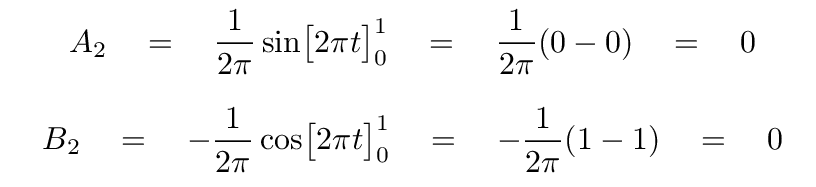
but the n=3 sine term is NOT zero.
So, to recap, at this point, we have
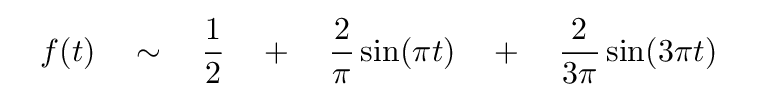
How well does this series reproduce the square wave?
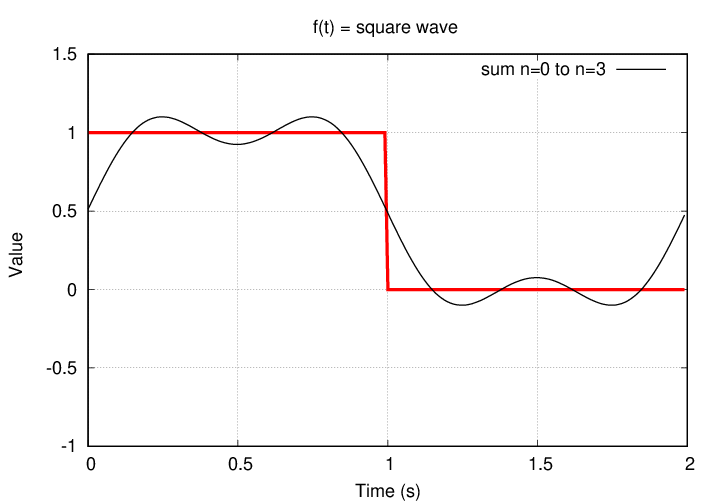
Note that the size of the n=3 coefficient is smaller than that of the n=1 coefficient. Hmmm. Does that presage a trend?
Only one way to find out. Time to solve for the n=4 ...
and n=5 terms.
Q: What are the values of A4 and B4? Q: What are the values of A5 and B5?
You should find that the n=4 coefficients are both zero,
but the coefficient of the sine term B5 is NOT zero. It is smaller than its preceding cousins, though.
Our approximation has reached
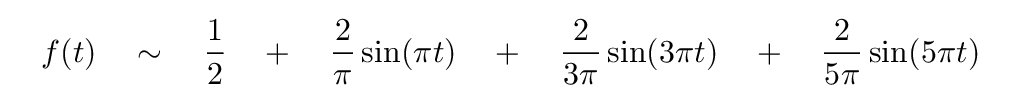
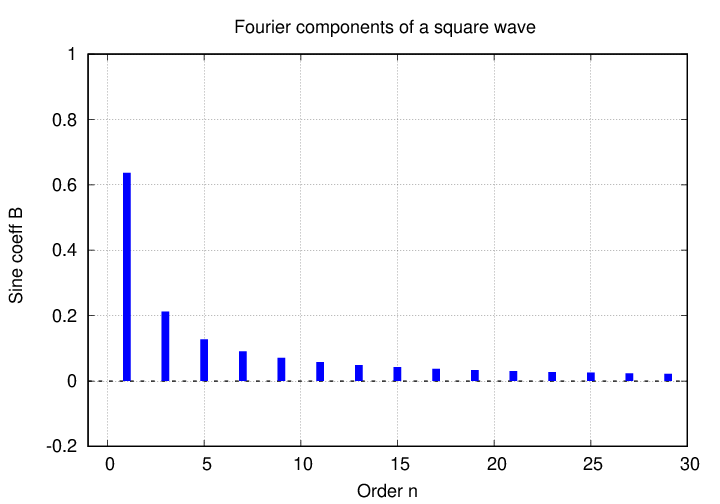
Note how the size of the coefficients is shrinking with n; this is a common feature of Fourier series. A graph showing the contributions of each term makes the same point: the quickly-wiggling lines have the smallest amplitude.
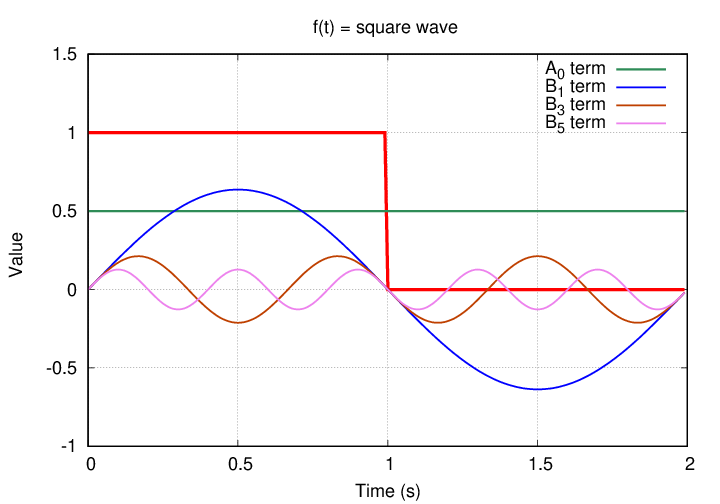
When we add those carefully weighted sine waves together, we get closer to the square wave.
If we include a LOT of terms, we can get pretty darn close to an angular square wave.
One way to express this Fourier expansion is to list the coefficients as text:
Another way is to make a graph which shows the value of each coefficient as a function of the value of n.
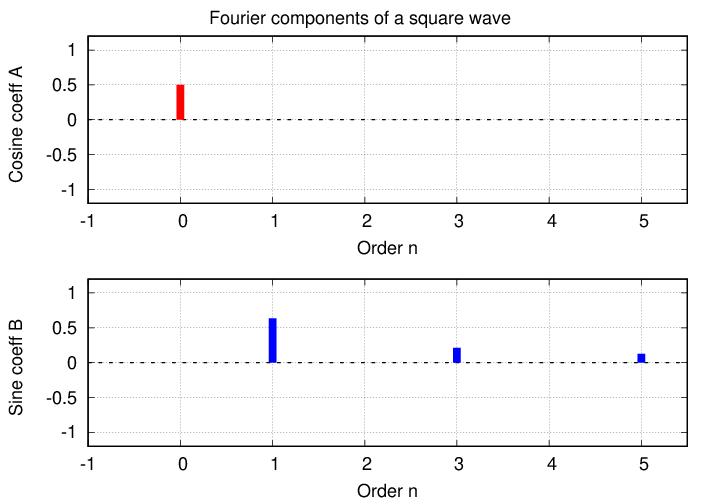
This sort of graph tells one very quickly which components contribute significantly to the Fourier series of a given function.
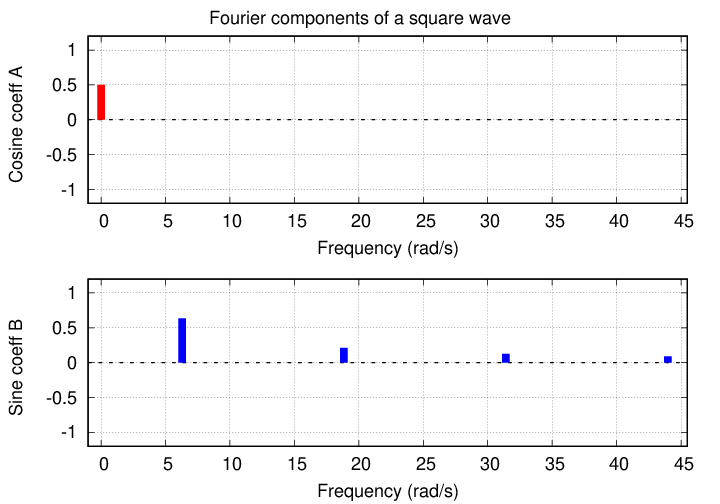
If we plot the value of each component against its frequency, the result is a frequency spectrum of the series.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.