 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Joe builds a mini-golf course for nerds. The fifth hole has a long fairway with a series of dips and rises, so that the height of the course follows a perfect cosine function.
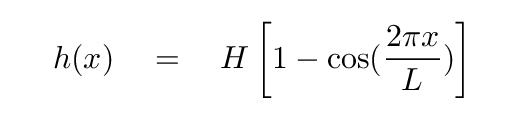
where
H = 0.2 m
L = 5.0 m
Viewed from the side, the course has an undulating appearance.
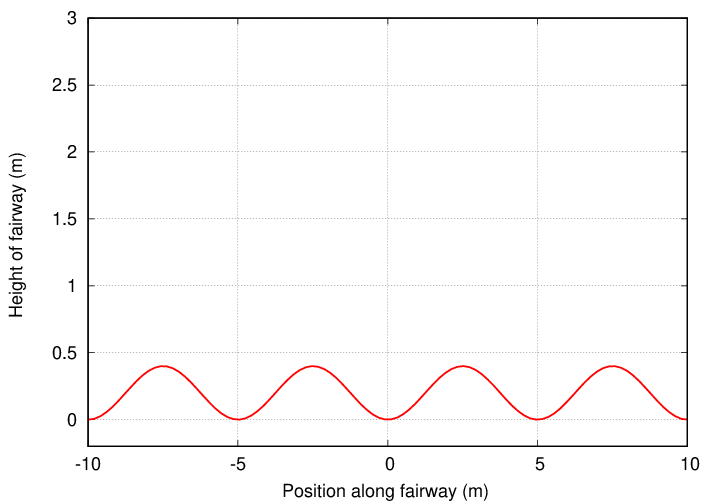
Suppose that a golf ball gets stuck in the "valley" in the middle of the course, at x = 0.
Q: If the ball is nudged a small distance to the side,
and the released, will it exhibit SHM?
Justify your answer.
One way to show that the ball would exhibit SHM is to verify that the potential energy has a quadratic form around its equilibrium point. Let's take a look.
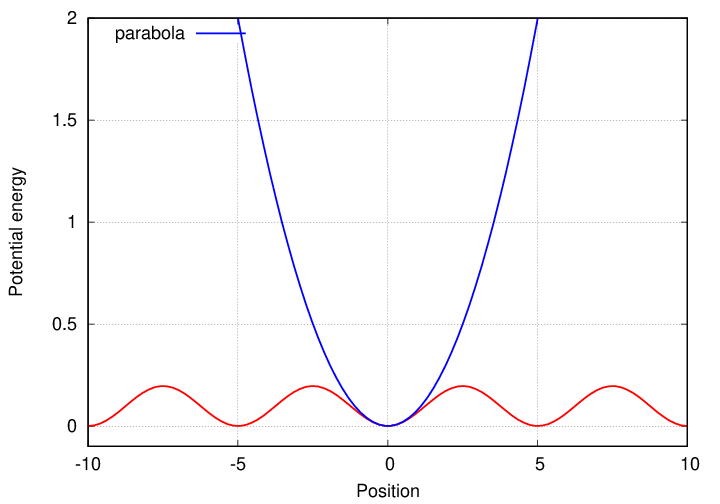
Q: If the ball is moved 3 meters to the right,
will it oscillate around the origin?
Q: What is the range of displacement which might
yield SHM?
Let's zoom in for a closer look:
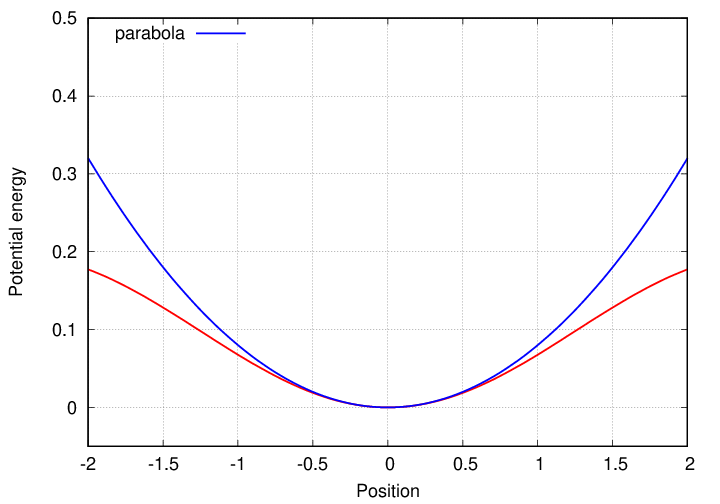
Q: If the ball is moved 1.5 meters to the right,
will it oscillate around the origin?
Q: Will that oscillation be SHM?
Q: What is the range of displacement which might
yield SHM?
Maybe we should move in even farther.

Great! Displacements on scales of this size, around 0.2 or 0.3 meters, seem to be "small" enough.
Q: How many radians, θ, in its cycle corresponds to a
horizontal displacement of 0.3 meters?
Q: What is the sine of this angular displacement θ?
Q: Compare the angle θ to sin(θ)
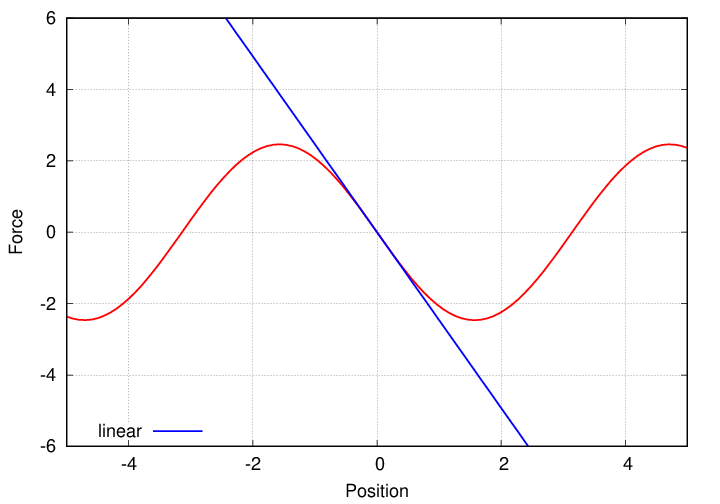
We can perform the same analysis by examining the forces on the ball near the equilibrium point, x = 0.
Q: What is the force, F(x), associated with this potential energy?
If we plot the force over a wide range of displacements from the equilibrium point, it doesn't look linear.
But if we zoom closer to the point of equilibrium, the force comes closer to a linear function.

And for "small" displacements, it is very close to the linear form required to yield SHM.
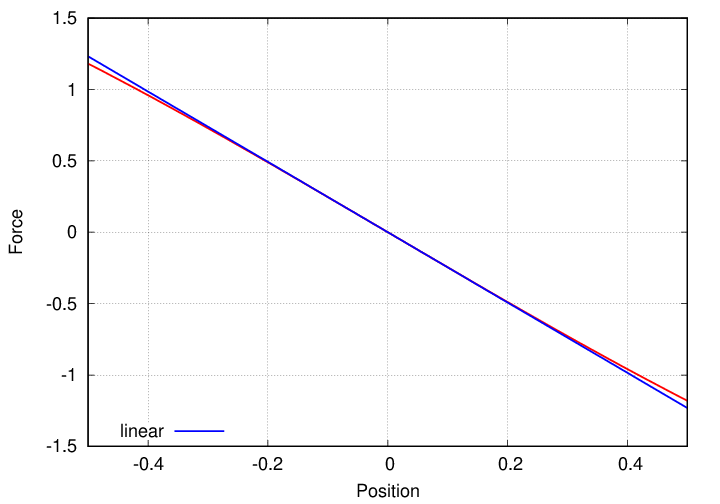
Q: If the golf ball is displaced by a sufficiently small
distance from x = 0, it will roll back
and forth in SHM. What is the period of that motion?
My answers in PDF or plain text
Today's main topic is a new way to write the equation of motion for an object undergoing SHM. It will help if we go back to a very simple example and review the "old" ways of writing the solution, before moving forward.
Suppose we set up a weight of mass m = 1 kg hanging from a spring of force constant k = 9 N/m. We will allow the weight slowly to pull down on the spring until it reaches an equilibrium, and we'll mark that location as y = 0. If we then pull the weight down a bit and release it, the weight will bob up and down. We can easily derive a relationship

which reveals that this is SHM with an angular frequency

We know already that we can write the position of the weight as a function of time in two "old" forms:
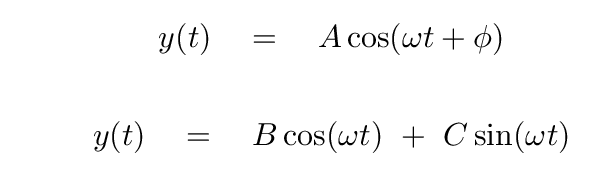
Let's pause for a moment to look at the constants A and φ (in the first form), and B and C (in the second form). How do we determine these values?
Well, note that everything we've done so far has been calculus -- involving differential equations and integrating and so forth.
But once we've written these equations for y(t), we move from the realm of calculus to the simpler realm of algebra. At this point, we need to bring into play the initial conditions of the situation. For example, suppose we measure the position and velocity at time t = 0 to be

Q: Use this information to determine the constants A
and φ in the first form.
Q: Use this information to determine the constants B
and C in the second form.
You should find

(though there are other equivalent expressions with different choices for the phase constant φ)
Okay, now we are ready for the NEW way to write the equation of motion for an object in SHM. Given the differential equation

we can also write the object's position as a function of time using an exponential form:
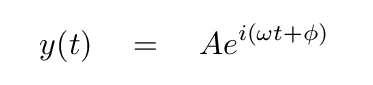
Note that there are still two constants of integration which will depend upon the initial conditions: A and φ.
But what does this mean? Can one really raise e to an imaginary power?
Yes, one can. The result is a complex quantity, which contains both real and imaginary components.

Well, a real mathematical proof is beyond my powers, but I can show a few pieces of information that might make this mysterious identity more palatable.
Remember Taylor expansions?
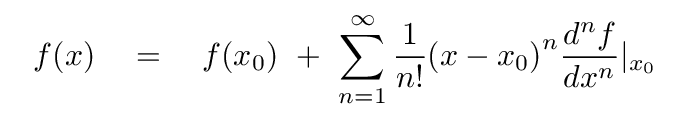
Let's review them for a couple of functions. In each case, we'll expand the function around the point x = 0.
Q: What is the Taylor expansion of cos(θ) around zero?
Gosh, half of the terms are just zero. And the signs alternate positive/negative/positive/negative ...

Q: What is the Taylor expansion of sin(θ) around zero?
Curious. Now the OTHER half of the terms are zero. And the signs also alternate positive/negative/positive/negative ...
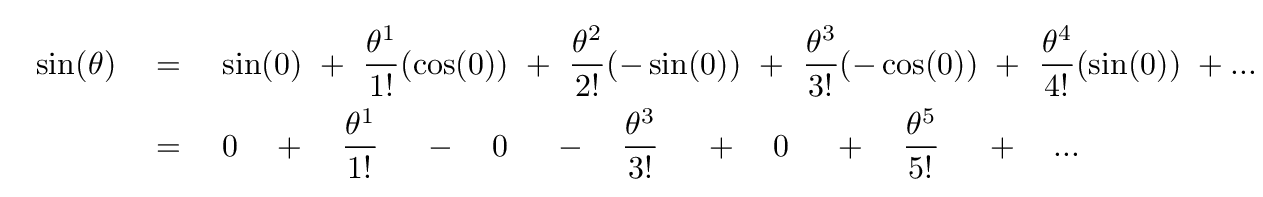
Hmmm. Is there other function that might yield a similar series -- but one which includes ALL these terms, added together? Let's see ... perhaps the function eiθ?
Q: What is the Taylor expansion of eiθ around zero?

Well, I'll be hornswoggled.
Okay, now that the mystery has been resolved, let's get back to representing SHM using this exponential notation.
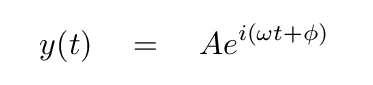
Q: Write the components of the complex quantity y(t)
corresponding to the exponential form of the solution
to our differential equation.
Right.

As you can see, this exponential form yields both a real and an imaginary component. MOST of the time, we will pay attention only to the real component, since most of the time, we will be concerned with real measurements.
In fact, the real component of this expression should look very familiar. It is exactly the same as one of the "old" ways of writing the solution. That's good -- all the ways of writing the solution should yield exactly the same result, after all.
But what's the point of this exponential notation? Why should we bother using it, if it simply reproduces one of the expressions we previously derived, and adds on second, imaginary component that we are (often) going to ignore?
There are at least two reasons to choose the exponential notation when dealing with problems involving vibrations and waves.
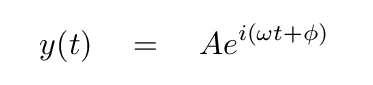
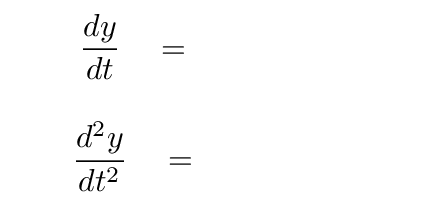
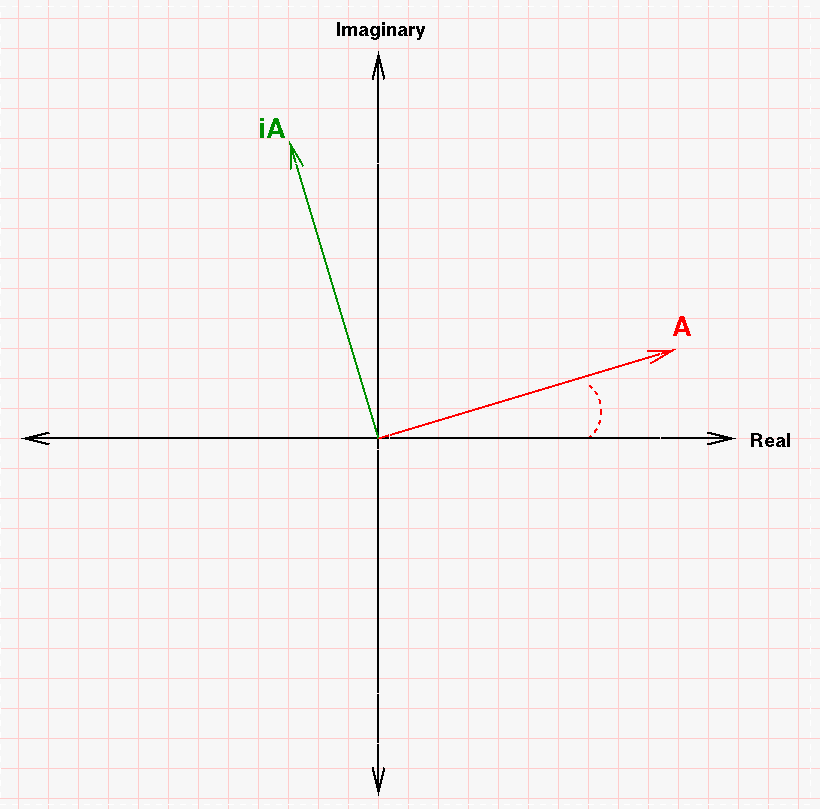
The complex plane is simply a 2-D plane which looks like the ordinary x-y plane, except that in this case, the horizontal axis represents the real part of a quantity, and the vertical axis represents the imaginary part.

To show a complex quantity on this plane, we draw a vector with the appropriate components.

Q: What is the complex quantity A shown above?
Now, it turns out that multiplying a quantity by i, the square root of negative one, changes its orientation in a simple way.
Q: What are the components of i times A?
As you can see, this new vector i A is just a copy of the original, rotated by 90 degrees.
Q: What happens if we multiply by i again?
That's right -- another 90 degree rotation. The result now points opposite to the original vector. But that makes sense, because i*i is -1, right?

Q: What happens if we multiply by negative i?
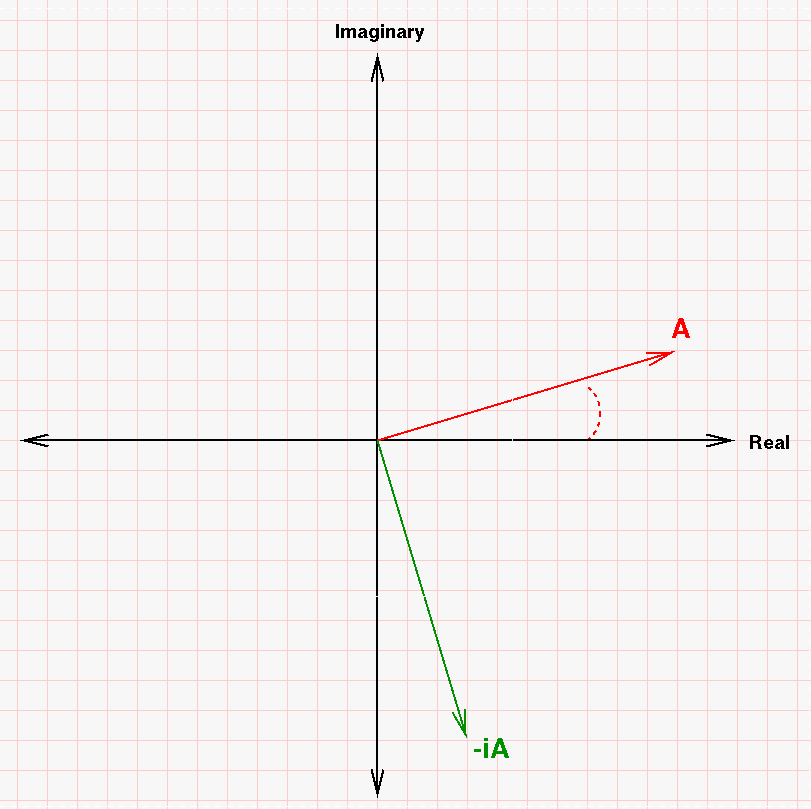
Sometimes, the angle of a vector θ in the complex plane is referred to as its phase or phase angle.
Okay, enough of a digression. Let's come back to the advantage of using exponential notation. Suppose that we describe the position of a weight hanging from a spring as
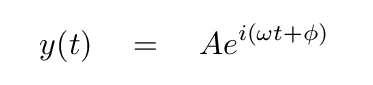
Then the velocity and acceleration of this weight must be
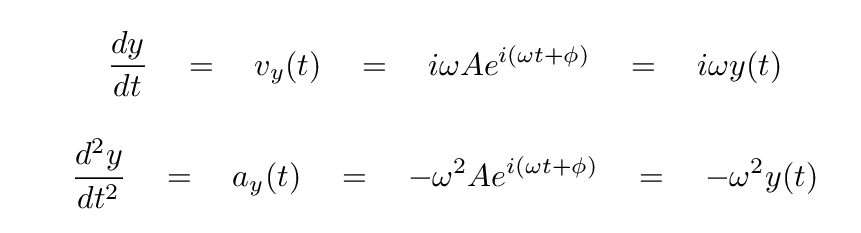
Q: How is the phase of the position related to the phase
of the velocity?
Q: How is the phase of the position related to the phase
of the acceleration?
Let's see if you were right. I'll use a set of real experimental data acquired in a UP I class back in 2009.
First, we can compare position to velocity ... Note that the period of the oscillation is about 1.1 seconds, which corresponds to a full cycle of 360 degrees of phase.
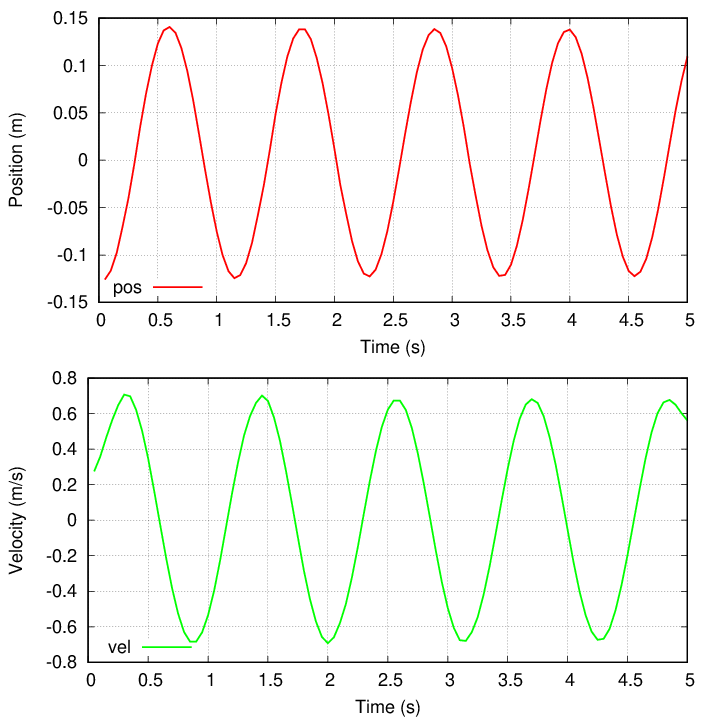
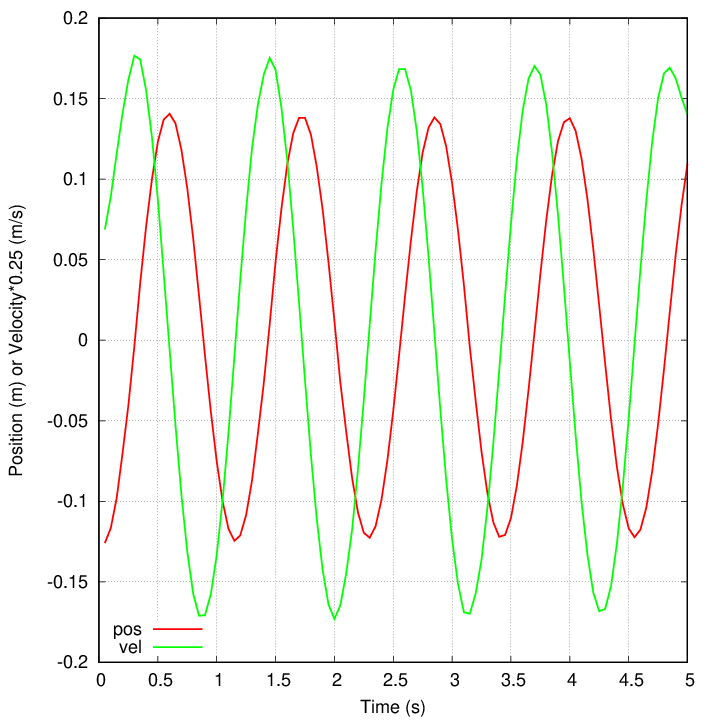
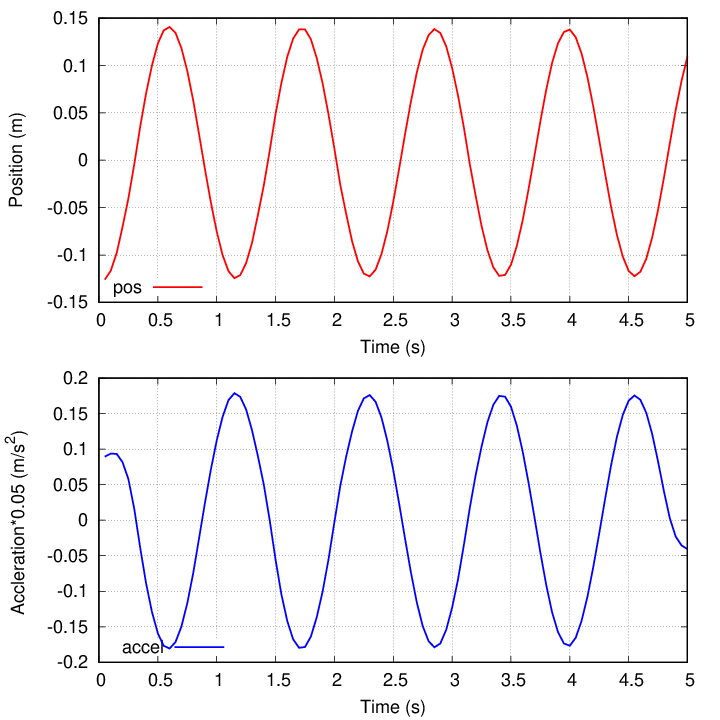
And now, we can compare position to acceleration ...

Let's do one simple example. Suppose that the position of the tip of a thin rod vibrates up and down so that its position is given by
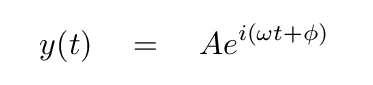
where
Q: At the time t = 5 seconds, what are the components
of the complex vector representing the position
of the tip of the rod?
Q: How long will it take from this moment (t = 5 s) until the rod
reaches its maximum height?
Note that although the position of the rod oscillates up-and-down, up-and-down, the vector representing its position in the complex plane rotates in a circle -- with exactly the same period and frequency.
This notion that SHM appears as a rotation in the complex plane leads us to one more way to write the general solution to our standard differential equation.
This equation has two constants of integration, the amplitude A and initial phase angle φ.
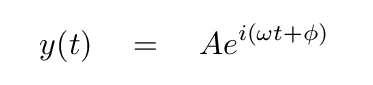
As time advances, the argument of the exponential increases, which means that the angle of the vector away from the real axis increases ...
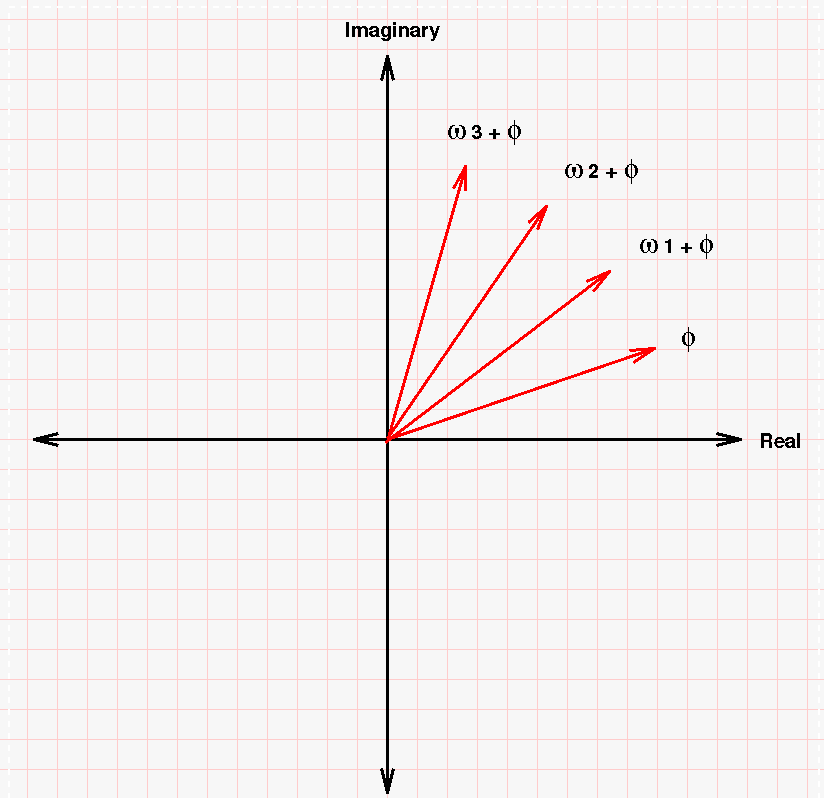
... which means that the vector rotates counter-clockwise.

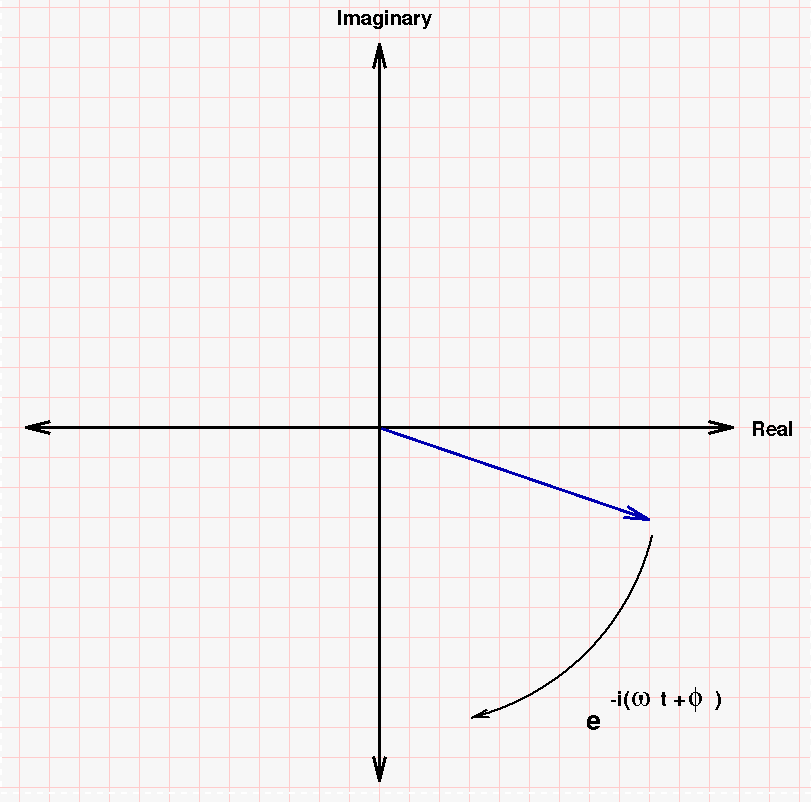
But the differential equation can also be satisfied if we make the argument to the exponential NEGATIVE.

That means that another possible solution to the differential equation is a vector in the complex plane which rotates CLOCKWISE.
And, just as we can write the general solution to SHM as a sum of a cosine plus a sine, replacing the phase angle φ with a second amplitude C,
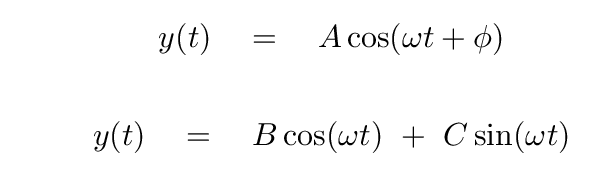
we can also write the general solution as the sum of a positive and negative exponential, again replacing the phase angle φ with a second amplitude C.
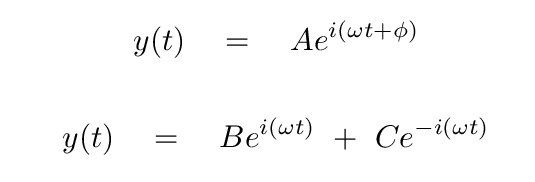

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.