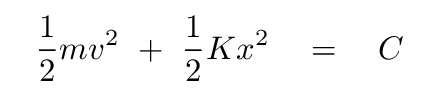
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Write a differential equation, involving position and its second derivative with respect to time, which gives rise to Simple Harmonic Motion.
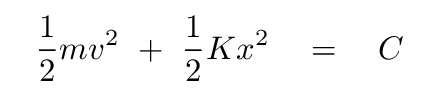
What does the above equation tell us about the energy of an object in simple harmonic motion?
a) the kinetic energy of the object is constant b) the potential energy of the object is constant c) the total mechanical energy of the object is constant
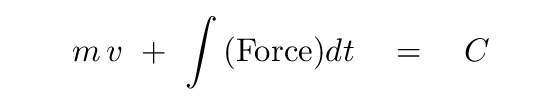
What does the above equation tell us about the momentum of an object in simple harmonic motion?
a) the momentum of the object is constant
b) the force on the object is constant
c) the change in the momentum of an object during some interval
is equal to the integral of the force on the object over that interval
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.