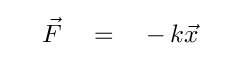
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Our standard situation for SHM involves motion around a stable equilibrium, in which a linear restoring force pulls the system back to the equilibrium point.
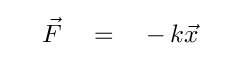
But in real life, other forces often play a significant role. It's difficult on Earth to escape from friction, or air resistance, or similar dissipative forces. Since these forces act to slow things down, we can represent them to a decent approximation by a force which is always opposite to the direction of motion.
Now, whether the new force acting opposite to motion is exactly linear with velocity is a good question. For objects moving through the air at slow speeds of a few meters per second, the force of air resistance is at least close to linear with velocity; moreover, the mathematics will work out nicely if we make this assumption.
Q: What are the units of b, the resistance coefficient?
So, let's move forward. I'll drop all the vector signs, as usual, for simplicity.
Q: Can you write the equation in differential form,
with all non-zero terms on the left, and zero on the right?
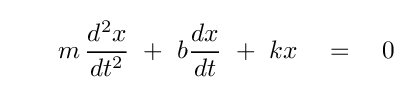
It's still a second-order differential equation for position as a function of time, but there's an extra term. The solution will no longer be a simple combination of sines and cosines, alas; so we can say goodbye to simple harmonic motion.
Q: What is the solution to this differential equation?
Hmmm. It's not obvious, but there are some clues.
Let's follow the time-honored tradition of guessing a solution, and then seeing if it works. How about a simple combination?
This version has the same old constants of integration, A and φ, which will depend on the initial conditions of the problem; and it has the same old frequency of oscillation, ω, which will depend on the properties of the system. But it now has one more parameter.
Q: What is the name of the new parameter? Q: What units does it have? Q: What does it mean?
We call τ the "time constant" of the system. It has units of seconds. If our guess turns out to work, then the amplitude of motion will decrease by a factor of 1/e every τ seconds.
Guessing is easy. Verifying that the guess is correct takes a bit of work. Let's get started.
First, we can make our lives simpler by writing the equation
in a more compact form, one which uses no explicit sines or cosines, but only exponential functions.
Q: Re-write the equation in terms of exponential functions only.
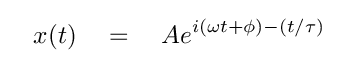
The first step in our verification involves writing down the first and second derivatives of x(t). Once we have them, we can plug them into the differential equation and see if they satisfy it.
Q: Write the first derivative, v(t) = dx/dt.
Q: Write the second derivative, a(t) = d^2x/dt2.
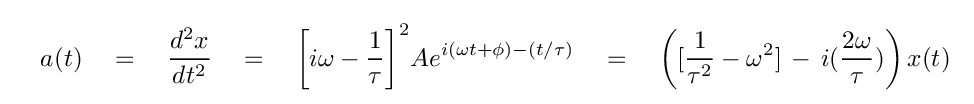
Right. We are now ready to place these expressions for the first and second derivatives into the differential equation that we HOPE our guess will solve.
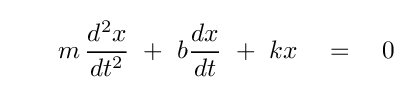
Q: Write the differential equation, using the above expressions
for the derivatives.
You should end up with something that looks like
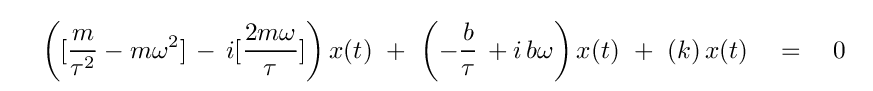
Phew. We aren't finished, but we're getting closer.
By the way, at this point, we have finished all the calculus needed for this problem. From this point forward, all that remains is algebra. Moving from calculus to algebra is a common feature of solving problems involving vibrations and waves ...
In order to satisfy the differential equation, the left-hand side of this expression must ALWAYS be EXACTLY ZERO. No matter what the time t might be, the result must be zero.
In order to make this true, we must ensure that two things happen:
Let's start with the imaginary coefficients.
Q: Write down the coefficients of all the imaginary terms in the equation
above.
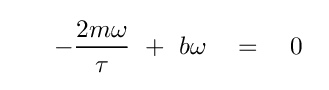
This tells us that the time constant τ must be related to the mass m and the coefficient of resistive force b like so (write this down -- will need it later):
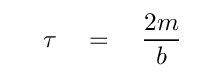
Q: What happens to the decay time if we increase the mass?
Q: What happens to the decay time if we increase the
resistive force?
Q: What happens to the decay time if the resistive force disappears?
All that is left is to figure out how to force all the REAL terms in the equation to add up to zero. I'll collect them all for you.
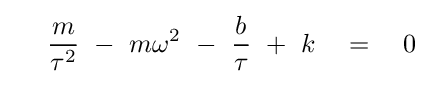
Now, we've just determined that the time constant must be
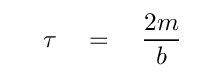
Q: Replace all occurences of τ in the equation above,
and then re-arrange terms to solve for the
value of the angular frequency ω.
You should find
So, as long as these relationships for the time constant τ and angular frequency ω hold, then our guess
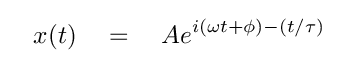
is indeed a solution to the differential equation.
Frame from
Monty Python and the Holy Grail
with words added
That expression for the angular frequency of the damped system should look somewhat familiar.
Q: What is the first term inside the square root?
Yes, that's the (square of the) angular frequency that a system WITHOUT DAMPING would have. If we write this as the "undamped frequency" ω0, then the frequency of the damped system is
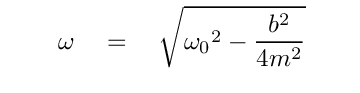
Now that we've found connections between the values of the physical constants m, k, b and the parameters of the solution τ and ω, we can explore how the system behaves under different situations.
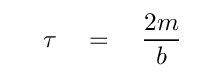
so if b = 0, the time constant τ goes to infinity. And that means that the equation of motion looks like
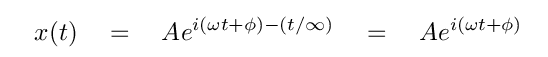
This is back to good old SHM, with frequency
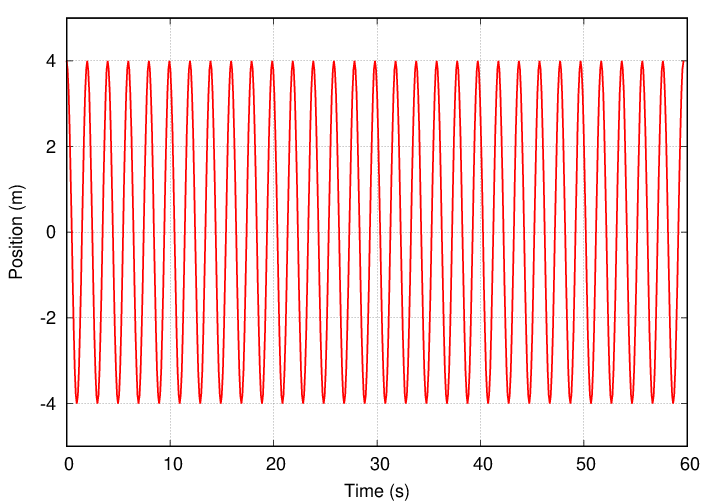
Q: What is the angular frequency ω for graph above?
We call systems like this underdamped.
The envelope of motion follows an exponential decay, with time constant τ.
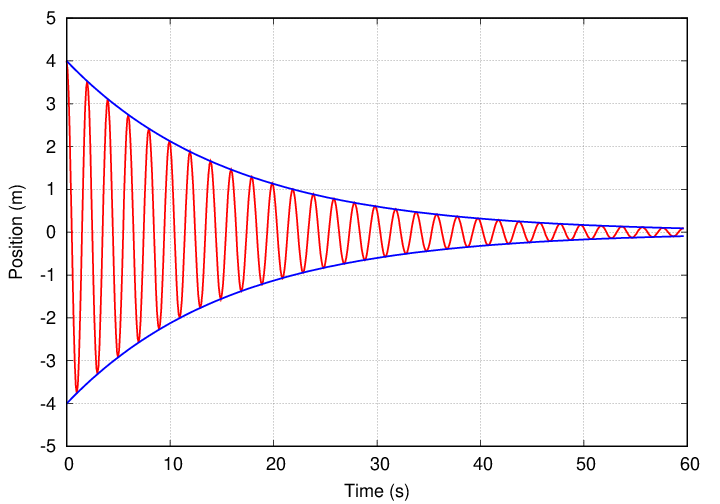
Q: What is the value of τ for the graph above?
Q: The mass of the weight is m = 1 kg.
What is the value of the resistive coefficient b?
Don't forget the units.
Look at the equation for the angular frequency of the damped harmonic oscillator. Something interesting will happen to this frequency if the value of b has a particular value.
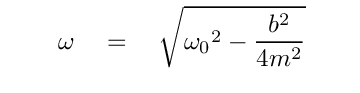
Q: What is the critical value of b?
Q: What happens if b has this value?
Yes, for critical damping, the equation of motion turns into
Note that ei φ is just a constant, not changing with time; we could call it C. So this equation becomes a simple exponential decay with no oscillation.
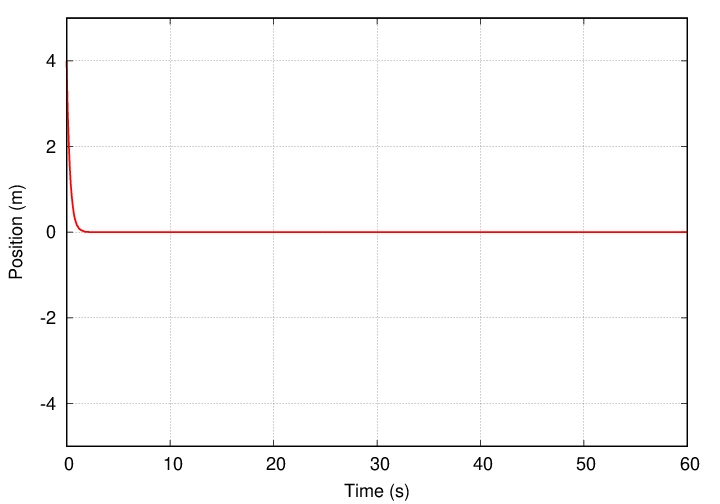
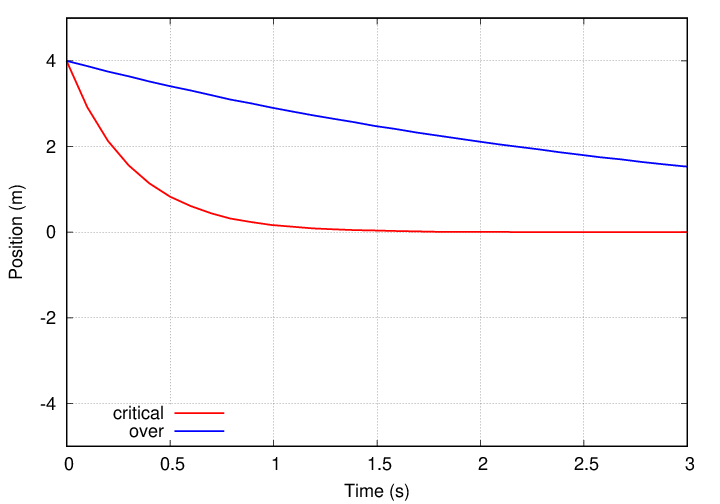
Critical damping turns out to be an important case in real life, because a critically damped system will return to equilibrium in the minimum possible time. So, for example, if you are designing shock absorbers for an automobile, you might choose materials so that, after the car has been jolted upward by a bump in the road, the spring returns quickly to its equilibrium position.
Actually, there is a second solution in this special case. One can also show that a function of the form
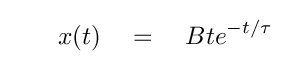
will satisfy the differential equation. So, the general equation of motion for critical damping is
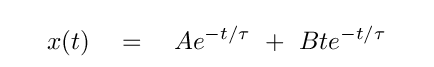
Okay, so what happens if we increase the damping even more? If b becomes large enough, then the term inside the square root becomes negative.
So that means that the angular frequency of oscillation becomes ... imaginary?
Sure, why not? For convenience, let's define a slightly different quantity that won't be negative
That means that the angular frequency can be written as
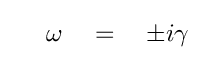
And we can just stick this expression for ω into our general equation of motion
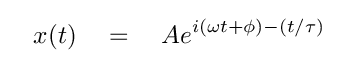
Q: After this substitution, what is the equation of motion?
Right. It's a sum of two terms, each of which is a non-oscillating exponential decay.
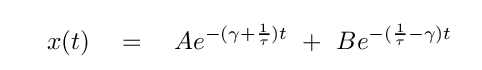
Note that this system will decay to equilibrium more slowly than a critically-damped system.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.