Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
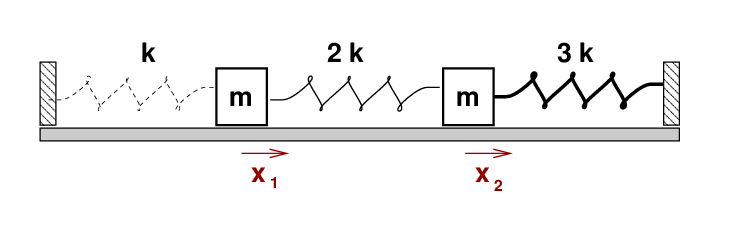
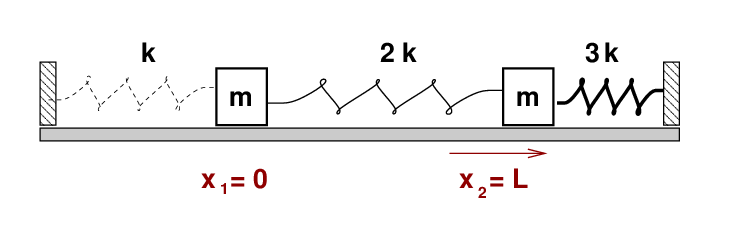
Today, we will work through one example of coupled oscillators. It might look familiar: two identical blocks of mass m sliding on a frictionless floor, connected by three springs:
But there's a difference: this time, the springs are NOT identical. Instead, they have three different force constants. From left to right, the values are k, 2k, and 3k.
What will happen if we displace these blocks from equilibrium and then release them?
We will carry out a series of steps to solve this problem. If you are faced with a similar problem, perhaps you could follow this template.
Yes, it's a lot of steps. But, after all, this is not a simple problem.
I've already drawn the picture -- just look above. Let's work through each of the subsequent steps in order.
Each block is pulled by two springs, one on the left and one on the right. Let us define
Then the forces on the left block are
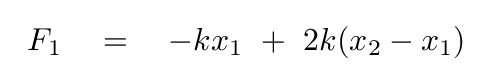
and the forces on the right block are
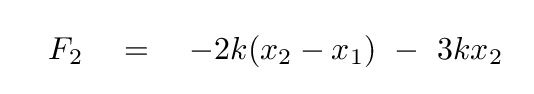
Let's collect all the terms involving the positions of the blocks.
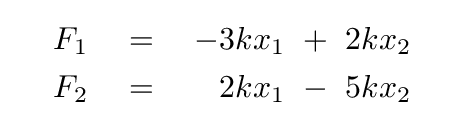
Now, the force on an object is simply its mass times its acceleration, so we can write the equations as
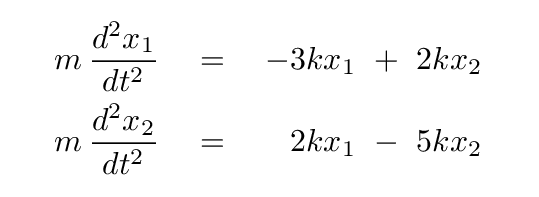
It will be convenient later to separate all the units from the numbers, so let's do that now by taking out a factor of k/m. Let's also put the derivatives on the right-hand side of the equation. With these simple re-arrangements, we can write Newton's Second Law in a matrix form like so:
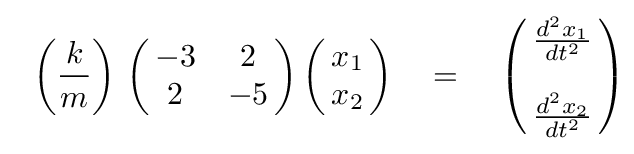
As this point, we will switch from using the actual coordinates of the blocks, x1 and x2, to a new set of variables. We hope that we may find a set of normal coordinates which will exhibit simple harmonic motion as the system oscillates; if we succeed, then we can describe ANY motion of the system as a sum of these very simple sinusoidal patterns.
So, let's define the normal coordinate
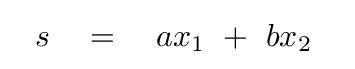
with the proviso that this particular combination of the actual positions does show simple harmonic motion; in other words, the second derivative of this combination with respect to time must be some negative constant times itself.
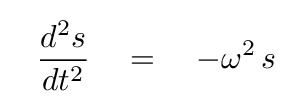
We can now re-write our matrix equation as
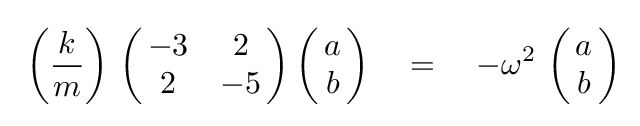
This will take a lot of work. Make yourself comfortable.
And now comes the hard part: in order to find the frequencies of the normal modes -- the values of ω -- we need to find the eigenvalues of the matrix. There are several approaches to this problem. I'll mention just two.
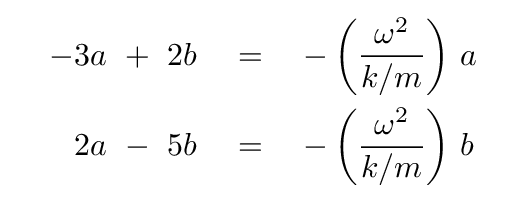
We can all the ordinary methods of solving two equations for two unknowns. For example, we can first solve one equation for b in terms of a
and then substitute that into the other equation. If all goes well, the result will have a factor of a in every term, so we can divide both sides by a and end up with something that looks like a quadratic equation:
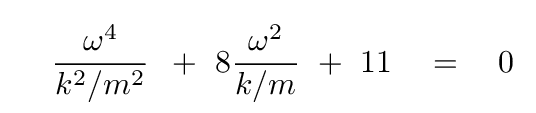
Q: Can you solve this quadratic equation for the
frequency ω in terms of k/m?
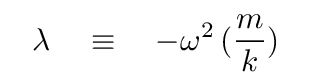
then we can write the matrix equation in a very standard form:
At this point, we move the λ term over to the left-hand side
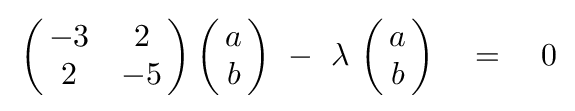
and merge the λ terms into the matrix:
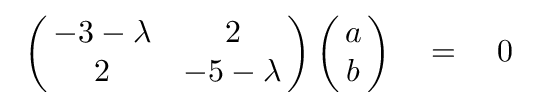
All we have done, really, is to isolate the matrix of numerical values -- which is based on particular masses and force constants in our physical setup -- and then to subtract some constant from the diagonal terms. The reason why we've gone to all this trouble is that setting the determinant of this modified matrix to zero will yield the eigenvalues we are seeking.
Q: What is the determinant of this matrix?
Right.
So, if we set that determinant to zero, we end up with a quadratic equation for λ.
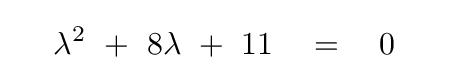
Q: Can you solve this quadratic equation for the
constant λ?
And, once we know λ, it's a simple matter to convert it to the angular frequencies of the normal modes; just invert the defintion of λ to find the angular frequency.
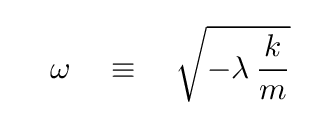
Either way, we can find the eigenvalues of this matrix, which yield the angular frequencies of the normal modes of the system:
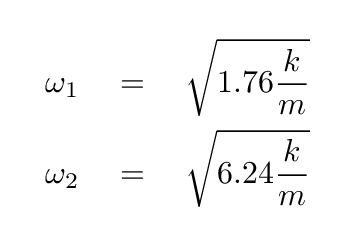
Our next task is to use each of the eigenvalues to find the corresponding eigenvector of the matrix. Each eigenvector tells us how to mix together the real coordinates, x1 and x2, in order to create the normal coordinates, s1 and s2.
We simply insert each eigenvalue into the right-hand side of the matrix equation,
and then solve for a in terms of b.
Q: Can you solve the first equation for a in terms of b? Q: Can you solve the second equation for a in terms of b?
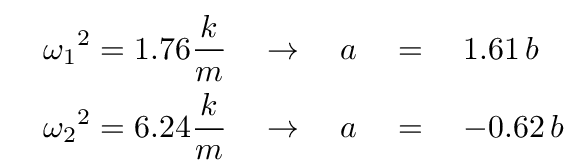
Now, recall our definition of the normal coordinates:
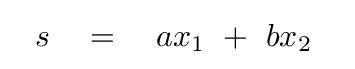
And so we conclude that the normal coordinates of this system must be
We have gone through a lot of work to figure out the properties of the normal modes of this two-block, three-spring system ... but now it finally pays off, as we can write a very simple pair of equations which describes its motion.
Very nice.
But ... what are the values of the 4 parameters A1, A2, φ1, φ2?
In order to attach values to these four parameters, we need to know more about the particular physical system that we are modeling. It will be sufficient if we are given a set of initial conditions, which specify the position and velocity of each block at some particular time.
For example, suppose that at time t = 0,
block 1 is at equilibrium position so x1 = 0
block 2 is moved to the right so x2 = L
block 1 is motionless so v1 = 0
block 2 is motionless so v2 = 0
First, we need to translate this information into terms involving the normal coordinates.
Q: What are the values for s1, s2?
Q: What are the values for ds1/dt, ds2/dt?
Good. Next, we can use these initial conditions to deduce the values of the four parameters in the general equation at time t = 0.
Q: What are the values for A1, φ1?
Q: What are the values for A2, φ2?
In some cases, this is as far as we need to go. We can describe mathematically the behavior of the system at any time.
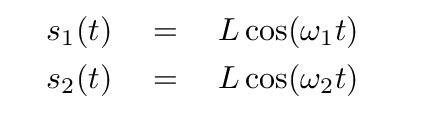
Sometimes, though, we need to take one more step. Suppose that we'd like to compute the position or velocity of one of the blocks at a given time. Our solutions so far are written in terms of the normal coordinates -- so, in order to find the position of a block, we need to convert those back into the original variables x1 and x2.
Recall
Q: Can your solve for x1 in terms of s1 and s2?
Okay, that's good. The final step is to use that expression, but replace s1 and s2 with their time-dependent equations we wrote in the previous section. In other words, to find an expression for x1(t).
Q: Can you write an expression for x1(t)?
One could, of course, do the same for x2. That is left as an exercise for the reader.
To check your understanding of this problem, here's a challenge for you. Suppose we are given the following values:
Can you solve for the position of each block as a function of time, and then make a graph showing the motions of each one? Your graph should
Label the graph with your name, and create a PDF copy of your graph. Send your work to the instructor via E-mail in order to receive extra credit.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.