The magnetic field created by a current

Purpose

To see how currents running through wires can create magnetic fields, and how the strength of those magnetic fields depends on distance from the wire.

What's the Point?

Even if you don't have a magnet, you can still create a magnetic field. The current passing through a wire will create a magnetic field near the wire. Ampere's Law can help you to figure out the strength of such a field in some circumstances.

Background Reading

Cutnell and Johnson, Chapter 21.7

Equipment

power supply
ammeter 0-3 A
8-10 patch cords
magnetic field probe
laptop with Vernier software
ruler

Procedure

Set up a current through a straight section of wire

Stick together 8 or so patch cords to make a long piece of wire. Connect it to a power supply and ammeter so that there's a straight section at least two feet long which sits as far from the power supply as possible, like this:

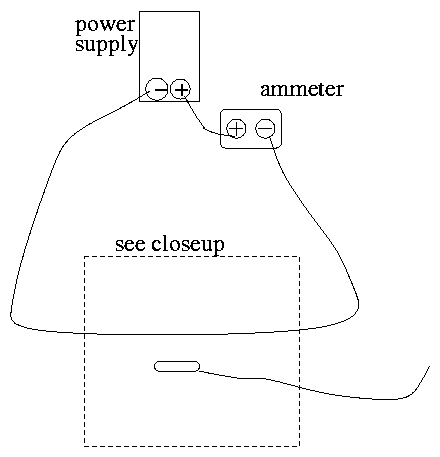
Turn on the power supply. Because the patch cords provide only a very small resistance, a large current will run through them. The power supply's built-in current limiter should activate -- you'll see the red bulb above "C.C." light up -- preventing the current from rising too high. Use the ammeter to read the current running through the wire. It should be somewhere between 1 and 3 amps. If the current is above 3 amps, adjust the power supply so that it goes down to 3 amps.

Prepare the magnetic field probe

Turn on one of the lab computers, and connect it to the Vernier controller. Plug in the magnetic field probe. Make sure that the toggle switch on the probe's black box is set to "Amplification = high x200". Start the Logger Pro program, and prepare to acquire data in the following manner: 20 samples per second, for 3 seconds. Verify that you can collect a set of data with the probe just sitting anywhere on the table. Use the Statistics function of Logger Pro to calculate the mean value of the magnetic field. What are the units?

Place the probe so that it lies parallel to the straight section of the wire. Twist the probe so that the white dot is pointing straight up, as shown.

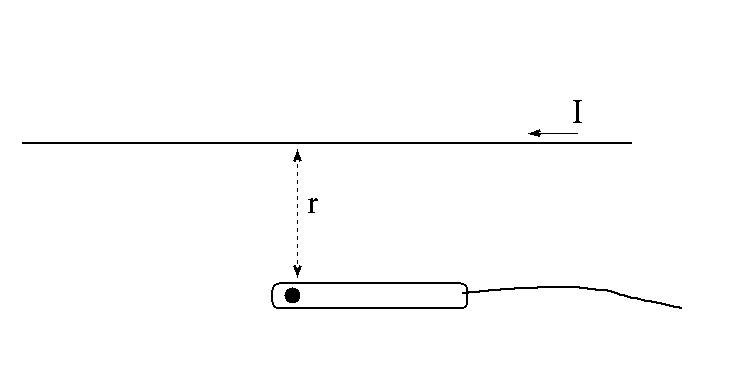
When the current is flowing, it will create a magnetic field around the wire. Which way will the magnetic field point? Indicate the direction of the magnetic field near the position of the probe in the figure above.

Measure the magnetic field when the power supply is turned off; you are detecting a "background" consisting of the Earth's magnetic field as well as components generated by electrical appliances in the room. Then turn the power supply on and measure the field again; your probe now detects the "background" plus the field generated by the current running through the wire. The difference between the two readings is the magnetic field created by the current in the wire alone.

Measure the magnetic field strength at a range of distances

You may have noticed that the magnetic field probe is very sensitive to its exact location and orientation. You are going to move the probe to different places near the wire, and that will cause the baseline reading of the probe to change. Go ahead and move the probe around on the tabletop, and watch its reading vary. How large are the changes from place to place?

In order to determine only the magnetic field produced by the wire, and not the changes in the ambient magnetic field, you need to make a differential measurement like so:

put the probe at some desired location
collect one set of data with the power supply turned off; take the mean value and call it B(off)
now turn the power supply on and collect another set; take the mean value and call it B(on)
calculate the magnetic field produced by the wire as B = B(on) - B(off)

Start with the probe on the side of the wire away from the power supply. Place it a distance of r = 20 cm and measure the field strength B. Write down your results. Then acquire more measurements at distances r of 18, 16, 12, 10, 8, 6, 5, 4, 3, 2, 1 cm.

Move to the other side of the wire

So far, the probe has always been on the same side of the wire, on the side far away from the power supply. What will happen if you move the probe to the other side, so it sits between the wire and the power supply? Predict the measurement you will obtain at a distance of 1 cm away from the wire on that other side.

Now, actually move the probe to the other side of the wire. Make sure that the white dot still faces straight up, and make the measurement. Was your prediction correct? If not, can you explain what changed as you moved the probe from one side of the wire to the other? Perhaps it would help to draw the direction of the magnetic field on both sides of the wire in the diagram above....

Make measurements on this other side of the wire at the same set of distances: 1, 2, 3, 4, 5, 6, 8, 10, 12, 16, 18, 20 cm.

Analysis

Analyze your results numerically

How does the strength of the magnetic field change with distance from the wire? It clearly becomes weaker with increasing distance ... but in what way? Is the relationship between magnetic field B and distance from the wire r

             B  =  k1 / r^2

or is it

             B  =  k2 / r

or perhaps

                         - r 
             B  =  k3 * e

One way to decide is to look at your data in a numerical fashion. Consider your measurement of B at the distance r = 3 cm. If the first model is correct, what should happen to the magnetic field strength if you double the distance? Should it be cut in half, or by some other factor? Then look at the measurement at double the distance, r = 6 cm. Does it agree with the model's prediction? What about the other models?

Pick at least ten different pairs of measurements in which one distance is an exact multiple of another distance.
Make a table in which you write down the distance and magnetic field strength for the first member of the pair. Add to the table the distance of the second member, plus the predicted field strength based on each of the three models above. Finally, note the actual measured B for the second distance in each pair. Your table should look something like this:
```
                                     predicted B2, for models   
             r1     B1       r2                         -r        actual B2
            (cm)   (mT)     (cm)      1/r^2    1/r     e            (mT)
       ------------------------------------------------------------------------
            
        
```
Compare the predictions in your table to the actual measurements at the second distance. Which model does the best job of reproducing nature?

Analyze your results graphically

Another way to compare models to a dataset is on a graph. Start by drawing axes on the graph paper provided. Place "Distance from the wire" on the horizontal axis, and "Strength of magnetic field" on the vertical axis. Use the absolute value of the magnetic field strength, so that all your measurements become positive numbers; do the same for your distances, too, if you recorded distances on the two sides of the wire with different signs. Figure out how large you'll have to draw each axis to contain all of your measurements, plus leave a little room for clarity.

Plot all your measurements on this graph. You should have two values at each distance, one from each side of the wire.

Now, how can we compare the models to the data on this graph? We will normalize all three mathematical functions,

             B  =  k1 / r^2


             B  =  k2 / r

                         - r 
             B  =  k3 * e

so that they match the graph exactly at one point, somewhere in the middle of the range. We'll use r = 4 cm as the point in common. Calculate the average value of your magnetic field strength at this distance. For each of the three functions,

use your average value of B and r = 4 cm to calculate the constant (k1 or k2 or k3) in the mathematical function
now that you have the constant, you can evaluate the function at any distance r. Calculate the value of the function at five or six other distances, covering the entire range of your graph. Place a small dot at each point.
draw a smooth line connecting these dots, and label the line so you know which function it belongs to

If one of the mathematical models is a good match to reality, then it ought to follow the actual measured values pretty closely. All of the lines will run through the data at r = 4 cm, but which of them does the best job of matching the data at other distances?

Discussion

Which of the three functions was the best fit to the actual strength of a magnetic field created by a long, straight wire? Is there another function you can devise which is fits the data better than any of the three?
Can you find any equation in your textbook which relates the current through a long wire to the magnetic field going around it? Does this equation have the same dependence on distance r as you determined empirically?
The equation in your textbook includes a number of factors which your empirical function lumped together as a single constant (k1 or k2 or k3). In a perfect universe, those factors would exactly equal your empirical constant; in other words, if you plugged into the textbook equation the values for the current through the wire, etc., you'd end up with exactly the magnetic field strength you actually measured.
How close does the textbook equation come to predicting your measured magnetic field values? Plot the textbook values as you plotted your measured values. Do you see a simple offset difference between the textbook values and your data, or a slope difference, or both? Calculate the percentage error between your measurement at r = 4 cm and the textbook's claim.
The most likely cause of this error is the absolute calibration of the magnetic field probes. Is your probe set to be too sensitive (gives a reading larger than the textbook prediction at r = 4 cm), or not sensitive enough (gives a reading smaller than the textbook prediction). Check with other groups in the room. Are all the probes mis-calibrated in the same direction, and/or by roughly the same amount?

Last modified 10/18/2003 by MWR