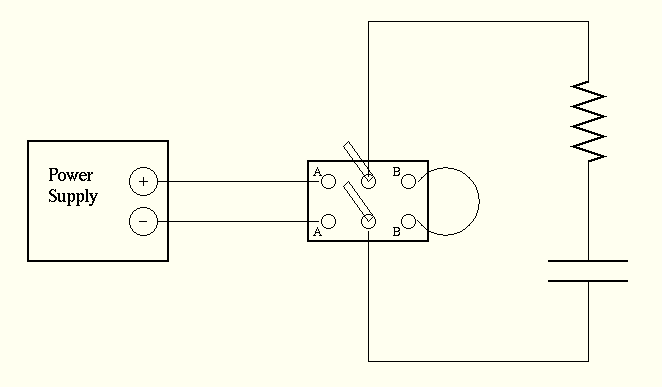
Figure 1
You will study the dynamic behavior of a series RC circuit by measuring the voltage across a capacitor as it charges and discharges. Graphical analysis of the data will reveal the time constant of the circuit, and the unknown resistances.
First, to see with your own eyes how RC circuits behave. Second, to give you some experience with exponential functions.
Capacitors: Cutnell and Johnson 19.5
RC circuits: Cutnell and Johnson 20.13

Examine the circuit diagram shown above in Figure 1. When the three-way switch is closed to the left, it completes a circuit in which current may flow from the power supply, through the resistor, and pile up on one plate of the capacitor; a corresponding amount of charge may be ripped from the other plate of the capacitor and flow back into the power supply. As time goes by, a equal and opposite charges +q and -q will build up on the plates of the capacitor.
Kirchoff's Loop Rule states that the potential drop across the resistance, I*R, plus the potential drop across capacitance, q/C, must equal the voltage V provided by the power supply; that is,
V = I*R + q/C
Since the current is the rate at which charges flow though the
circuit,
dq
I = ----
dt
this expression represents a differential equation in q.
dq q
V = -- R + ---
dt C
The solution yields the charge on the capacitor as a function of
time; specifically,
-t/τ
q = Q { 1 - e } Q = C*V, τ = R*C
max max
Using this result, one can determine the expression for the voltage across the plates of the capacitor as a function of time; specifically,
-t/τ
V = V { 1 - e } τ = R*C
max
where Vmax is the voltage given by the power supply.
This relation indicates that the voltage across the capacitor will start at 0 and increase quickly at first, then more slowly. It will approach the value Vmax but never quite reach it. Over a time interval of one time constant τ = R*C, the difference between the voltage and Vmax is decreased by 63% = (1 - 1/e).
If you can fit an exponential curve of form
-t/τ
V = V { 1 - e }
max
to the data values for voltage as a function of time,
you can determine the time constant.
If you know the time constant and the capacitance C,
you can figure out what the resistance R must be.
On the other hand, if you throw the switch to the right, then you remove the power supply from the circuit, and complete a short circuit running in a circle around the resistor and capacitor. This will discharge the capacitor: the charge which was stored on its plates will now run back together, bringing the capacitor back to a neutral state. In this case, the voltage across the capacitor ought to decrease:
-t/τ
V = V e τ = R*C
max
One can fit an exponential function to this data to find the time constant. It ought to agree with the time constant measured as the capacitor was charged.
You should complete all the following steps by the end of your class period. They are explained in detail below.
Be sure to answer all Questions in your lab report.
The power supply should be arranged properly before you start the experiment. Ask the instructor if it is necessary to set it up as described below.
First, you must set the power supply to provide a constant voltage of about 3 volts.
- Turn all knobs on the power supply counterclockwise to their "zero" positions.
- (if available) Use a digital multimeter to measure direct-current voltage from the positive to the negative terminal of the power supply: attach the appropriate leads directly to the terminals.
- Turn on the power to the power supply.
- Turn the coarse current knob about one-quarter of a turn clockwise.
- Now, while watching the multimeter's display, carefully turn the voltage knobs clockwise until the meter reads three volts, or something close to it. Write down this voltage for future reference. If you don't have a digital multimeter, just set the knob so that the needle display on the front panel of the power supply reads about 3 volts.
- The green light on the the front panel of the power supply should be lit -- that means that the voltage will provided by the power supply will remain constant throughout the experiment.
- Disconnect the multimeter from the power supply and turn it off; we won't need it for a while.
If you choose the Series RC icon to start the Logger Pro program, it should perform all the steps below automatically. The instructions are included below just in case something goes wrong.
First, you need to set up the Logger Pro program to read data from the voltage sensor.
- Your computer should be powered up, and you should see the Windows NT desktop. If not, turn on the computer's power, and ask the instructor to log in.
- Launch the application Logger Pro from the icon on the computer desktop.
- From the menu, choose Setup, then Sensors.
- Click on DIN1 and set sensor to "Voltage" (this is the default setting for DIN1). The computer will automatically choose a calibration file.
- From the menu, choose Experiment and Sampling. Take three samples of data per second. Try setting the experiment's duration to 30 seconds; if that doesn't seem long enough, change it later.
- From the menu, choose View and Graph Options. Remove the check mark next to "Connecting Lines", and place a check mark next to "Point Protectors". This will make your data appear on the graph as little boxes, without connecting lines.
- At this point, you should see a Red Collect button at the top of the screen, alongside the menu controls File,Edit, etc. If you do not see a Collect button, then Save the current session into a file on disk, then quit and re-start Logger Pro. This is a known bug :-(
The circuit may already be built for you when you start. If not, follow the steps below.
Now build the circuit shown in Figure 1. You should have a plastic box, inside of which is a Y-shaped section of wire with a capacitor and two branches with resistors:
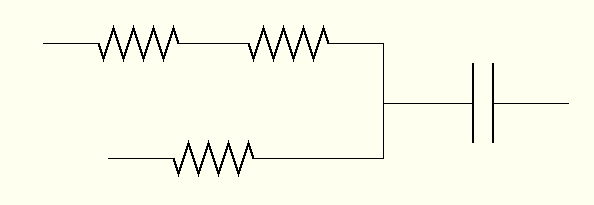
Figure 2For this part of the experiment, connect the branch of the wire containing one resistor, as well as the branch containing the capacitor. You'll use the other branch, with two resistors, later on.
Leave the switch in its "Open" position, with the handle straight up, so that there is no complete circuit.
Connect the voltage sensors to your circuit. Make sure that the red sensor is attached to the positive side of the capacitor (marked with a little "+" plus sign).
Discharge the capacitor by throwing the switch to the right; this will complete a short circuit, and any charge on the capacitor's plates will (eventually) neutralize itself. Wait about one minute for this to occur.
Okay, you're ready to make some measurements!
You should see voltage increase from an initial value of zero up to some maximum value ... which should be the same as the voltage provided by the power supply.
Question: why does the voltage measured across the capacitor approach the same value as the voltage provided by the power supply?
Fiddle with your graph so that it shows the entire dataset. You can modify the limits of the graph in each direction by double-clicking on the axes.
Make two simple sketches of the circuit which is completed when you throw the three-way switch to the left. Each should include the power supply, resistor, and capacitor. Indicate on your drawing
Call one sketch the "Just Closed" version -- show on it the direction the current is flowing, and the direction the electrons are moving, immediately after you have closed the switch. Call the other sketch the "After" version -- show on it situation at the end of the charging process.
The Logger Pro program provides a mechanism to fit data with various mathematical functions. You may use it to figure out the time constant of your circuit as it charges, or you may choose to use Excel or some other program familiar to you. If you choose to use Logger Pro, then you should
A * { 1 - exp(-C*x) } + B
1
τ = R*C = ---------
fitted "C"
Question: What is the time constant of your circuit, based on the data taken while charging the capacitor?
It would be wise to save your data at this point. Please save all data to a floppy disk, rather than the hard disk of the computer.
Now, prepare to discharge the capacitor. Before you can take data, you must
You should see voltage now decrease from an initial value (which should be the same as the voltage provided by the power supply) down to zero, or close to zero.
Fiddle with your graph so that it shows the entire dataset. You can modify the limits of the graph in each direction by double-clicking on the axes.
Make two simple sketches of the circuit which is completed when you throw the three-way switch to the right. Each should include the resistor, capacitor, and short-circuit wire. Indicate on your drawing
Call one sketch the "Just Closed" version -- show on it the direction the current is flowing, and the direction the electrons are moving, immediately after you have closed the switch. Call the other sketch the "After" version -- show on it situation at the end of the discharging process.
Now try to determine the time constant of your circuit from the voltage during the discharge.
A * { exp(-C*x) } + B
1
τ = R*C = ---------
fitted "C"
Question: What is the time constant of your circuit, based on the data taken while discharging the capacitor?
Question: Do the two values of time constant agree with each other? What is the percent difference between them? If the difference is larger than you expected, try to explain it.
It would be wise to save your data at this point. Please save all data to a DIFFERENT file(s) on the floppy disk -- don't overwrite your first results!
If you want to impress your instructor, and you have time, you might make two (or three) sets of measurements while charging the capacitor, and two (or three) while discharging. Comparing the time constants from each run might give you some idea for the uncertainty of the value from a single run.
At this point, you should know the time constant τ = R*C for the circuit with a single resistor. You can read the capacitance from the surface of the capacitor.
Question: Calculate the resistance of the single resistor.
Write down your answer to the question above.
Now check it: throw the three-way switch to its middle position, breaking the discharge circuit. Then use the digital Fluke multimeter as an ohm-meter to measure the resistance across the single resistor.
Question: How close was your calculation to the actual resistance of the single resistor?
The other branch of your RC segment contains two resistors. Each of them is identical to the single resistor you have already used.
Question: What is the resistance of the double-resistor branch? If you were to connect it to the circuit, instead of the single-resistor branch, what would the time constant be?
Write down your answer to the question above.
Now test your prediction: change your circuit so that it runs through the double-resistor branch, instead of the single-resistor branch, of the wire.
Analyze your data as before -- fitting an Inverse Exponential Function to these measurements.
Question: What is the time constant of this new double-resistor circuit? Does it match your prediction?
Save the data from Run #3 onto a floppy disk.