THE DIFFRACTION GRATING SPECTROMETER

PURPOSE:

In this experiment you will study the operation of a diffraction grating spectrometer. After calibrating the instrument you will measure the wavelengths of the first four lines of the Balmer se- ries of hydrogen and compare your results to the predictions of Bohr model.

WHAT'S THE POINT?

To see how one can measure, quantitatively, the wavelength of a beam of light, using a simple instrument on a table top.

BACKGROUND READING:

Bohr model of the atom: C&J 30.3
Line spectra: C&J 30.2
Diffraction: C&J 17.2, 17.3, 27.5, 27.7. See Figures 27.37 and 27.38

APPARATUS:

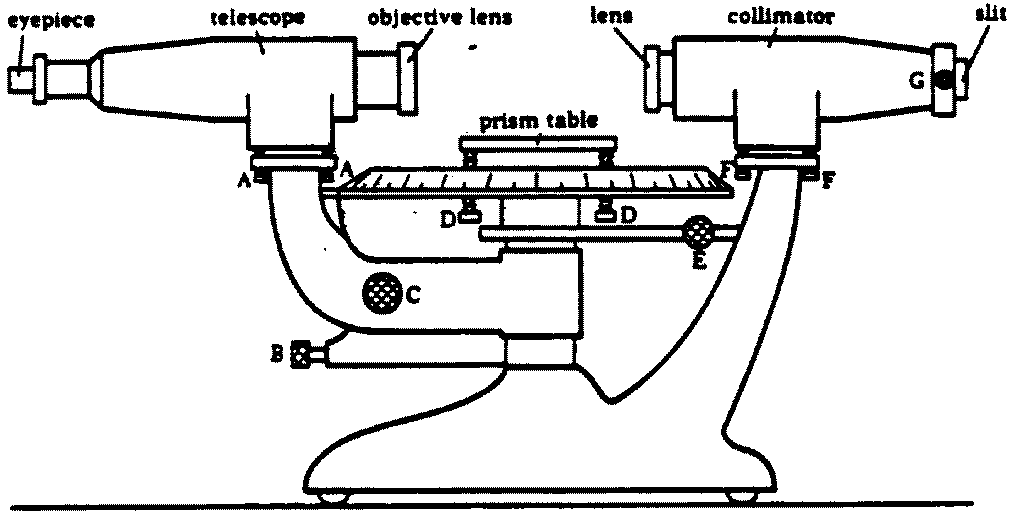
The essential parts of the spectrometer are shown in Figure 1.

A sketch of a spectrometer showing the various adjustments A; Screws to level or align the telescope B; Knob to fix the position of the telescope. This knob must always be loosened before moving the telescope by hand and locked only to make fine adjustments with knob C. C, Fine adjustment knob. S, Screws to level or raise the prism table. E, Knob to fix the position of the graduated disc and prism table. When readings are taken with the telescope, this knob must be in the locked position. F, Screws to align the collimator. G, Knob for adjusting the slit width. The slit should be wide enough to allow a sufficient amount of light to pass through but as narrow as possible to allow accurate measurement.

The spectrometer has around its base a scale graduated in degrees, with a least count of half a degree. There is also a vernier scale above the main one, which runs from 0 to 30, subdivided into smaller units; this vernier scale measures arcminutes. Recall that there are 60 arcminutes in a degree.

In order to take a reading of the angle at which the spectrometer is set, do the following:

1. Take a reading from the main scale: read the number opposite the marking "0" on the vernier scale. Make sure you choose the half-degree which is SMALLER than the "0" on the vernier scale. This yields the angle to the nearest half-degree.

2. Take a reading from the vernier scale, which gives the number of arcminutes away from the half-degree determined above. Add this number of arcminutes, divided by 60, to the main reading.

Example: a student find that the value 156.5 on the main scale is closest to the "0" on the vernier (without going past the "0"). She then looks at the vernier and chooses 17 as the best match on that scale. The total angle is

       angle = 156.5 degrees + (17/60) degrees = 156.78 degrees.

THEORY:

The diffraction grating is discussed in detail in your text. Despite its great simplicity, the diffraction grating spectrometer is a very precise measuring instrument, and it is still the most commonly used device for measuring the wavelengths of spectral lines.

If parallel light of wavelength w is incident normally on a grating, then the angle theta at which the intensity of the transmitted light is a maximum is given by the grating equation

     d sin(theta)  =  n w,       n  =  1,2,3...                 (1)

In the equation d is the spacing between the slits of the grating, and the integer n is the order number. The grating spectrometer permits very precise determination of the angle theta. If the grating spacing d is known, then w can be calculated.

Historically, the diffraction grating spectrometer was in use long before the line spectra emitted by atoms were understood. In 1885, Balmer found a simple mathematical expression which described some of the wavelengths of the lines observed to be emitted by hydrogen. There was no explanation of why those particular wavelengths were emitted until the advent of the Bohr model in 1913.

The wavelengths of the Balmer series are given accurately by the simple formula

              1     1
     1/w = R(--- - ---),  m = 3,4,5...                       (2)
             2^2   m^2

                   7    -1
     R = 1.097 x 10    m                                     (3)

PROCEDURE:

1. Before the spectroscope is used, the telescope must be adjusted to focus parallel rays, and the collimator must be adjusted to give parallel rays. These adjustments have been made already. All you need to do is adjust the eyepiece so that the cross hairs are in good focus.

2. After making the adjustment in procedure (1), place the diffraction grating on the spectrometer table. Make the plane of the grating perpendicular to the axis of the collimator.

3. Turn on the mercury light source and set the telescope cross hairs on the central image produced by the grating. This is the zero angle reference needed for future measurements. Make sure that the telescope is adjusted so that both the cross hairs and the slit are in focus. Adjust the location of the light source in front of the slit to give the brightest possible image. To be certain the grating table is level, look at all the lines on both sides of the central maximum. The lines should be at the same height on the two sides. If they are not, you should level the grating table.

4. Some common pitfalls or problems:
   • It's easy for stray light to make faint spectral lines invisible. Make sure that the door to the lab is closed, the window shade is drawn and fastened to the wall, and the door's window shade is also drawn.
   • The spectrometer used by one group of students may accidentally point towards the gas tube of another group of students, and show IT as a bright line. Make sure that each group shields its instrument from all others.
   • Some of the lines described in below (especially the violet lines of hydrogen and the blue-violet lines of mercury) are very hard to see.
   • Some gas tubes may give poor results. Try getting a new tube if one particular setup fails to show most of the lines.
   • If the diffraction grating is mounted the wrong way, no spectrum appears. If no spectrum appears, try rotating the grating by 90 degrees in its holder.
   • The slit-adjustment knobs on some of the spectrometers will only increase the slit width; in order to narrow the slit, you must first turnthe knob in the correct direction (although the slit width won't shrink), and then push the slit jaws very gently together.

5. Measure the angles of the first order maxima for the two yellow, one green, one blue-violet, one violet lines of the mercury spectrum. Measure the angles of the maxima on both sides of the central maximum. Be sure to use the vernier when measuring angles. Record your data in the data table. Use these data to calculate the grating spacing d for the grating you are using.

   Note: Usually, the violet line is to dim to be seen. Sometimes there is a fuzzy green line in this spectrum; do not measure it. If you cannot see two yellow lines, your slit is probably too wide; adjust the width to make the slit narrower.

6. Remove the mercury light and replace it with a hydrogen light. If you examine the hydrogen spectrum, you will observe a red, a blue-green, a blue-violet, and a violet line. (Often the violet line is too dark to be seen.)

7. Measure the angle of the first order maxima on both sides of the central maximum. Record your data.

8. Measure the angle of the second order maxima on both sides of the central maximum. Record your data.

CALCULATIONS:

1. Deduce the grating spacing d using the measurements made of the mercury spectrum. Note that the units of d are the same as the units used for wavelength w In this lab, we use Angstroms to measure wavelength: 1 Angstrom = 10^(-10) meters.

2. Complete the data table containing the hydrogen spectrum measurements. Compute the wavelengths and their uncertainties. Compare your experimental values to the theoretical values given.


             DIFFRACTION GRATING SPECTROMETER  


Date__________                       Name_______________________________
                                     Lab Partner(s)________________________


Measuring Devices              I.D. No.      Range               Least Count
==============================================================================

Angle Scale on Spectrometer








                               Data Table

1.  Mercury Spectrum

------------------------------------------------------------------------------
color   wavelength   theta      theta       theta     sin(theta)        d
                          Left       Right       avg           avg
        (Angstroms)  (degrees)  (degrees)   (degrees)               (Angstroms)
______________________________________________________________________________

Violet       4047
______________________________________________________________________________

Blue-violet  4358
______________________________________________________________________________

Green        5461
______________________________________________________________________________

Yellow (1)   5770
______________________________________________________________________________

Yellow (2)   5790
______________________________________________________________________________


   Average Value of d = _______________




2. Hydrogen Spectrum

------------------------------------------------------------------------------
color       order  theta      theta       theta     sin(theta)      wavelength
              n         Left       Right       avg           avg
                   (degrees)  (degrees)   (degrees)                (Angstroms)
______________________________________________________________________________

Violet        1  
______________________________________________________________________________

Blue-violet   1
______________________________________________________________________________

Blue-green    1
______________________________________________________________________________

Red           1
______________________________________________________________________________

Violet        2
______________________________________________________________________________

Blue-violet   2
______________________________________________________________________________

Blue-green    2
______________________________________________________________________________

Red           2
______________________________________________________________________________


  For comparison, the actual wavelengths of Hydrogen lines are:

        Violet:       4102   Angstroms
        Blue-violet:  4340   Angstroms
        Blue-green:   4861   Angstroms
        Red:          6563   Angstroms

  How close were your measurments in each case?