Exponential Decay

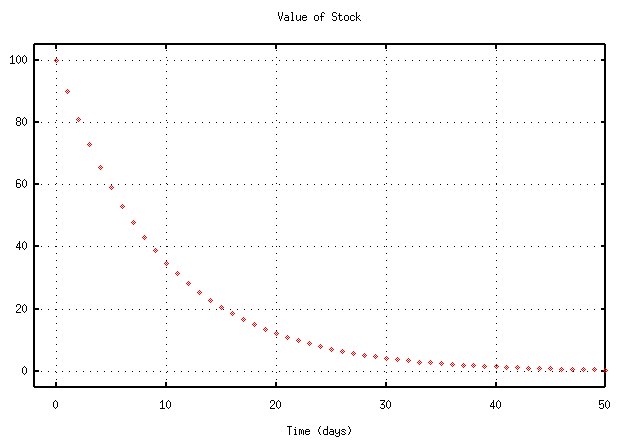
Joe Moneybags invests $100 in the stock of a certain energy-trading company. He watches the value of his stock day-by-day for a month.

  day    stock value
----------------------
   0.0   100.00 
   1.0    90.00 
   2.0    81.00 
   3.0    72.90 
   4.0    65.61 
   5.0    59.05 
   6.0    53.14 
   7.0    47.83 
   8.0    43.05 
   9.0    38.74 
  10.0    34.87 
  11.0    31.38 
  12.0    28.24 
  13.0    25.42 
  14.0    22.88 
  15.0    20.59 
  16.0    18.53 
  17.0    16.68 
  18.0    15.01 
  19.0    13.51 
  20.0    12.16 
  21.0    10.94 
  22.0     9.85 
  23.0     8.86 
  24.0     7.98 
  25.0     7.18 
  26.0     6.46 
  27.0     5.81 
  28.0     5.23 
  29.0     4.71 
  30.0     4.24 

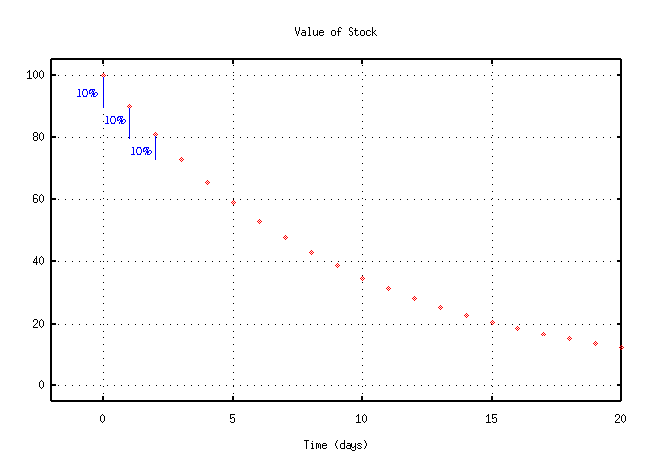
Stockbroker Number One says, "The value decreases by about 10 percent of its current value each day. Another way to say that is that the stock keeps 90 percent of its value after each day. You could describe it mathematically like this:"

      original                 $100.00
      after one day            $100.00 * (0.90)
      after two days           $100.00 * (0.90) * (0.90)
      after three days         $100.00 * (0.90) * (0.90) * (0.90)
        ...
                                               x
      after x days             $100.00 * (0.90) 

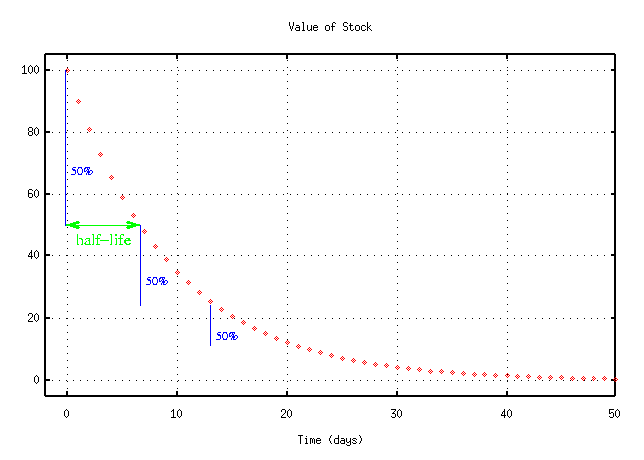
Stockbroker Number Two says, "The value decreases by about 50 percent of its current value each day. Another way to say that is that the stock keeps 50 percent of its value after 6.5 days. You could describe it mathematically like this:"

      original                 $100.00
      after 6.5 days           $100.00 * (0.50)
      after 13  days           $100.00 * (0.50) * (0.50)
      after 19.5  days         $100.00 * (0.50) * (0.50) * (0.50)
        ...
                                               x/6.5
      after x days             $100.00 * (0.50) 

A scientist might call the time it takes the stock to decrease to half its current value the half-life of the stock. In this case, the half-life of the stock is about 6.5 days.

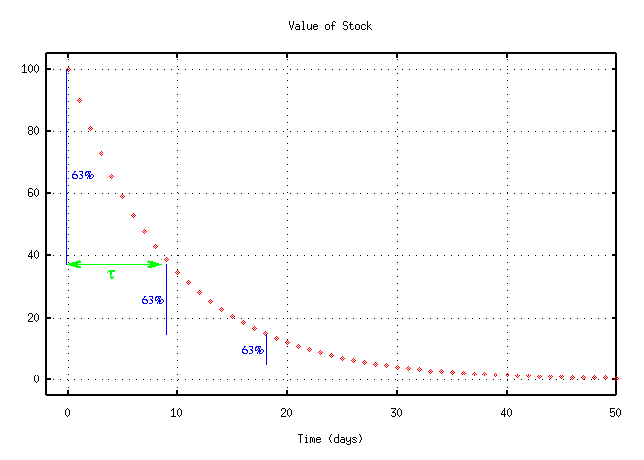
Stockbroker Number Three says, "The value decreases by about 63 percent of its current value every 9 days. Another way to say that is that the stock keeps 37 percent of its value after each day. You could describe it mathematically like this:"

      original                 $100.00
      after 9   days           $100.00 * (0.37)
      after 18  days           $100.00 * (0.37) * (0.37)
      after 27  days           $100.00 * (0.37) * (0.37) * (0.37)
        ...
                                               x/9 
      after x days             $100.00 * (0.37) 
  or
                                               x/9 
      after x days             $100.00 * (1/e ) 
  or
                                            -x/9 
      after x days             $100.00 * (e) 

Here, e = 2.71828... is the base of the natural logarithms; your calculator probably has a button to raise e to any given power. A scientist might call the time it takes the stock to decrease to 1/e its current value the e-folding time of the stock. Another scientific term for the time it takes a quantity to fall to 1/e of its original value is time constant, often represented by the Greek letter tau .

                                            -x/(time_constant)
      after x days             $100.00 * (e)